Goldilocks域

1. 引言

Goldilocks域 $p=2^{64}-2^{32}+1$，目前用于Polygon生态的多个项目中：

• Polygon Miden VM：在https://github.com/maticnetwork/miden 中使用了winterfell项目的winter-math库：https://github.com/novifinancial/winterfell/blob/main/math/src/field/f64/mod.rs（Rust语言）
• Polygon Zero Plonky2：https://github.com/mir-protocol/plonky2/blob/main/field/src/goldilocks_field.rs（Rust语言）
• Polygon Hermez 2.0：https://github.com/0xPolygonHermez/goldilocks（C++语言）

以Goldilocks域 $p=2^{64}-2^{32}+1$ 为base prime field的椭圆曲线有：

• 1）Cheetah curve：
  • 2022年论文 Security Analysis of Elliptic Curves over Sextic Extension of Small Prime Fields
  • https://github.com/ToposWare/cheetah （Cheetah curve实现，Rust语言）
  • https://github.com/ToposWare/cheetah_evidence （Cheetah curve安全性论证，Python和SageMath）
• 2）ecGFp5 curve：
  • 2022年论文 EcGFp5: a Specialized Elliptic Curve
  • https://github.com/pornin/ecgfp5（ecGFp5 curve实现，Rust和Python）

$p=2^{64}-2^{32}+1$，${\mathbb{F}}_p^{\ast }$的order为$p-1$，即：
$2^{64}-2^{32}=2^{32}\cdot 3\cdot 5\cdot 17\cdot 257\cdot 65537$
即意味着该域具有$2^{32}$-th root of unity。
相应的generator为：
$g=7$
$2^{32}$-th root of unity 为$g^{(p-1)/2^{32}}=0x185629dcda58878c=1753635133440165772$。
相应的sage脚本为：

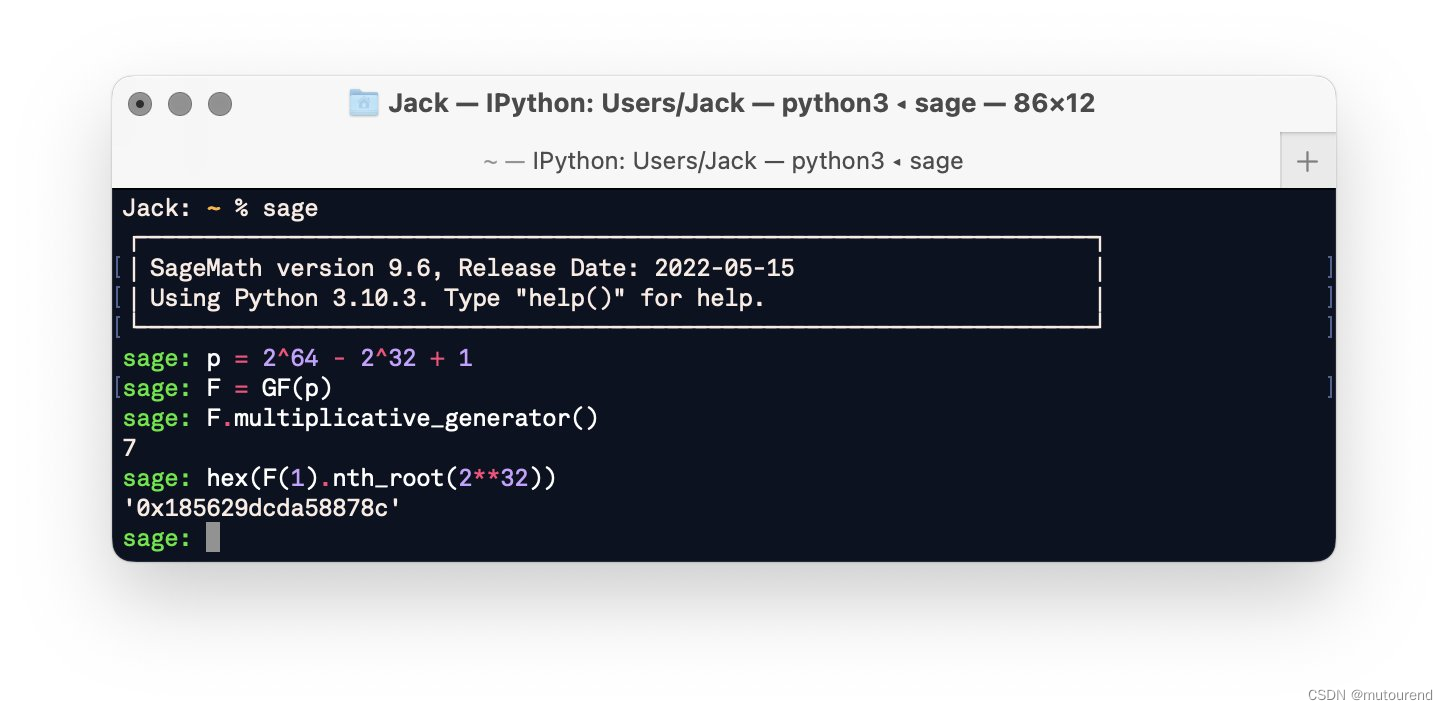
1.1 乘法运算之Goldilocks域 vs. BN254域

根据Ariel Gabizon twitter有：

• 1）采用A100 GPU，Goldilocks域乘法运算比BN254域快15.5倍：
  • BN254: ~34*10^9 muls/s
  • Goldilocks: ~527*10^9 muls/s
• 2）大多数CPU上，单个Goldilocks乘法运算需约2~3 cycles，256-bit乘法运算约需要80~100 cycles。
• 3）根据polygon zkEVM repo，在AMD EPYC 7773Xc处理器上，Goldilocks域乘法运算比BN254域快约9倍。在该及其上采用的是Karatsuba算法来对n-digital long integers进行乘法运算。
• 4）根据UIvetanna——ZKP加速（获得Bain Capital Crypto、Paradigm以及Jump Crytpo联合的1500万美金种子轮投资）的FPGA开发，Goldilocks域乘法运算的延迟要比BN254快约8倍，资源利用率要比BN254好10~15倍。

2. Why Goldilocks？

STARKs/SNARKs处理常规整数运算的难点在于：

• 所有的值都是以有限域元素表示。
• 将有限域运算 映射为 32-bit或64-bit整数运算 是昂贵的。（注意：EVM使用256-bit整数）

Miden VM原生支持所有32-bit unsigned integers（u32）运算，从而使得相应的运算效率很高：

• 每个u32运算仅需要一个VM cycle。

Goldilocks域 $p=2^{64}-2^{32}+1$，具有一些很好的特性：【详细见：u32 operations in Miden VM 】

• 1）值适于64-bit整数，从而使得基于该域的运算在现代CPU上运行很快。
• 2）2个32-bit整数乘法不存在域模溢出问题。
• 3）检查4个16-bit values是否构成了一个有效filed element 的效率可以很高。

Miden VM中的大多数u32运算（包括bit shifts、bit rotations、value comparison）仅需要少量的16-bit range checks。对于一些复杂的运算（如bitwise AND/OR/XOR），需要使用辅助lookup tables，但是这些复杂运算也是efficient的。

参考资料

[1] twitter u32 operations in Miden VM
[2] u32 operations in Miden VM
[3] cronokirby 2022年9月1日博客 The Goldilocks Field
[4] twitter Goldilocks Field