博弈论中的MinMax搜索算法

博客参考：https://blog.csdn.net/tangchenyi/article/details/22920031

极小极大算法常用于二人博弈游戏，目的是寻找最优的方案使得自己能够利益最大化。基本思想就是假设自己（A）足够聪明，总是能选择最有利于自己的方案，而对手（B）同样足够聪明，总会选择最不利A的方案。

下面举个例子进行说明：
设：正方形代表自己（A），圆代表对手（B），节点的每个孩子节点代表一个候选方案。

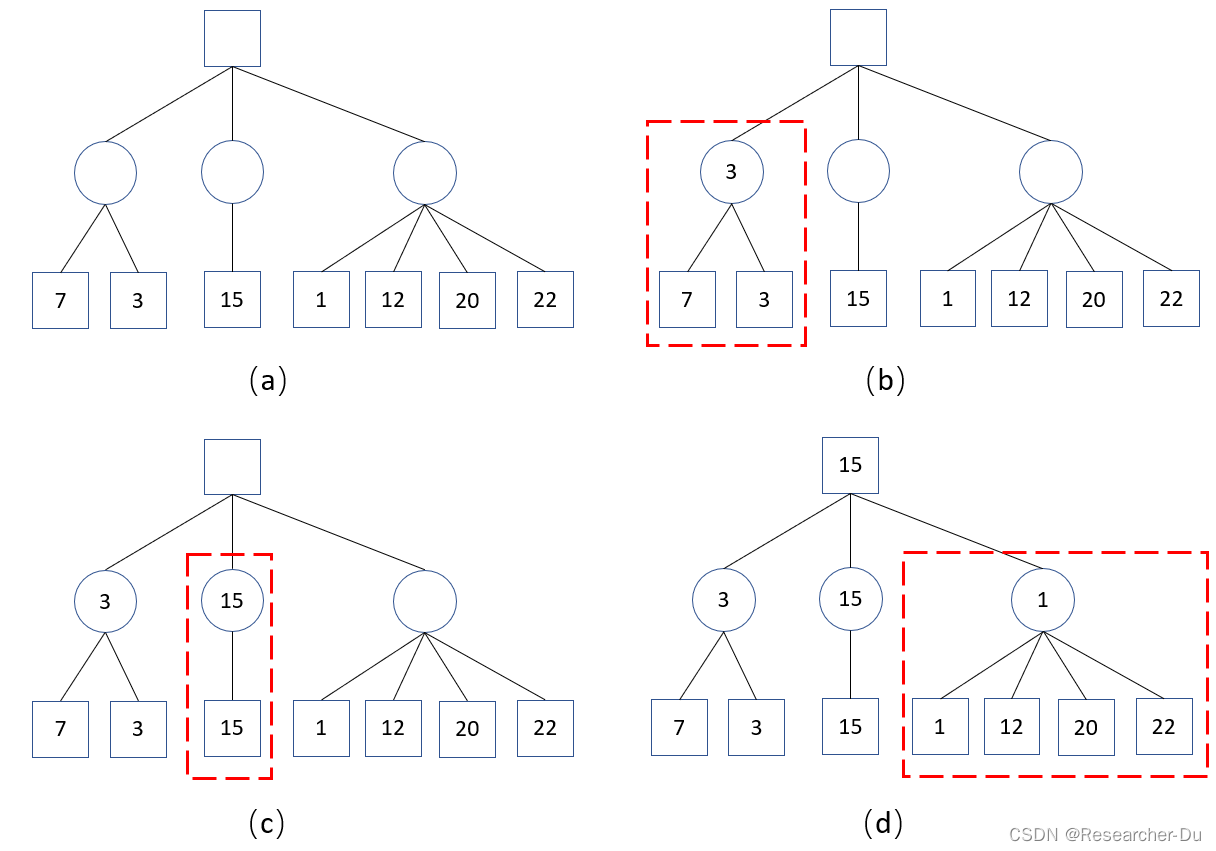
图（a）：显示了所有候选方案。让我们如下分析：（注意：图中的所有数字都是A的利益值，越大越有利于A）
图（b）：假设A选择第一个方案，B有两个候选方案，B为了使得A利益最小化，所有在7和3中选择了3，所以A只能获得3。
图（c）：假设A选择第二个方案，B只有一个选择，A最终可以获得15。
图（d）：假设A选择第三个方案，B有4个可选方案，为了使得A利益最小，B选择第一个方案，则A只能获得利益1。
A为了使得自己利益最大，所以A会选择第二个方案，即获得利益15。
从上图可以看出，B总是选择候选方案中的最小值，而A总是选择候选方案中的最大值，极小极大的名字也就源于此。

该算法使用深度优先搜索（Depth First Search）遍历决策树来填充树中间节点的利益值，叶子节点的利益值通常是通过一个利益评估函数算得。

下面给出一个具体的井字棋的例子：

#include 
#include 
using namespace std;

char board[3][3];

void init() {
    for (int i = 0; i < 3; i++)
        for (int j = 0; j < 3; j++)
            board[i][j] = '_';
}

void draw_board() {
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++)
            cout << board[i][j] << " ";
        cout << endl;
    }
    cout << endl;
}

int game_result(){
    for (int i = 0; i < 3; i++){
        int r =  board[i][0] +  board[i][1] + board[i][2];
        int c =  board[0][i] +  board[1][i] + board[2][i];
        if (r == 3 * 'X' || c == 3 * 'X') return 0; 
        if (r == 3 * 'O' || c == 3 * 'O') return 1;
    }

    int d1 = board[0][0] + board[1][1] + board[2][2];
    int d2 = board[0][2] + board[1][1] + board[2][0];
    if (d1 == 3 * 'X' || d2 == 3 * 'X') return 0;
    if (d1 == 3 * 'O' || d2 == 3 * 'O') return 1;
    return -1;
}

//评估函数：电脑赢：空格数+1, 玩家赢：-空格数-1,平局：0 
int eval() {
    int res = 0;
    for (int i = 0;i < 3;i++)
        for (int j = 0;j < 3;j++)
            if (board[i][j] == '_') res++;

    int flag = game_result();
    if (flag == 1)  return res + 1;
    if (flag == 0)  return -(res + 1);
    return 0;
}

//从当前状态开始DFS搜索最优的落子位置：电脑最大化收益，人最小化收益。
int MinMaxSearch(int& pos, int step) {      //step：记录层数,奇数层为电脑操作,偶数层为玩家操作  
    int val = step & 1 ? -100 : 100;        //奇数层取极大值,偶数层取极小值
    if (game_result() >= 0) return eval();  //游戏结束，评估分数

    vector<int> ava_pos;    //记录还有那些位置可以下棋
    for (int i = 0; i < 3; i++)
        for (int j = 0; j < 3; j++)
            if (board[i][j] == '_') ava_pos.push_back(i * 3 + j);
    if (ava_pos.size() == 0) return eval(); 

    for (int i = 0; i < ava_pos.size(); i++) {
        int x = ava_pos[i];
        int t = x;
        board[x / 3][x % 3] = (step & 1) ? 'O' : 'X';
        int son_val = MinMaxSearch(x, step + 1);
        board[t / 3][t % 3] = '_';

        if (step & 1) {
            if (val < son_val) {
                val = son_val;
                if (step == 1) pos = ava_pos[i];  //初始状态下的最优孩子节点（落子位置）。
            }
        }
        else  val = min(val, son_val);
    }
    return val;
}

int main() {
    init();

    for (int i = 1; i <= 9; i++) {
        //电脑下棋=============================================================
        cout << endl << "computer move:" << endl;
        int computer_pos; 
        MinMaxSearch(computer_pos, 1);
        board[computer_pos / 3][computer_pos % 3] = 'O';
        draw_board();

        //玩家下棋=============================================================
        printf("Select a position(1~9):");
        int x; cin >> x; x -= 1;
        while (1) {
            if (x > 0 && x < 10 && board[x / 3][x % 3] == '_') break;
            printf("The position is not available！please reselect.\n");
            cin >> x;  x -= 1;
        }
        board[x / 3][x % 3] = 'X';
        draw_board();

        //判断游戏是否已经结束=================================================
        int Winer = game_result();
        if (Winer >= 0){
            Winer ? printf("You lose！\n") : printf("You win！\n");
            return 0;
        }
    }
    printf("平局\n");

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111