数据结构与算法--001--时间和空间复杂度

时间复杂度

若存在函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数，记作T(n)=O(fn)，O为算法的渐进时间复杂度，简称为时间复杂度。

空间复杂度

若存在函数f(n)，使得当n趋近于无穷大时，S(n)/f(n)的极限值为不等于零的常数，则称f(n)是S(n)的同数量级函数，记作S(n)=O(fn)，O为算法的渐进空间复杂度，简称为空间复杂度。其中，f(n)为算法所占存储空间的函数，n为问题的规模。

时间/空间复杂度的表示原则

1. 如果运行时间/空间是常量级，则用常数1表示
2. 只保留函数中的最高阶项
3. 省略最高阶项前面的系数

举例：
T(n)=100n，不满足原则1，原则2：最高阶为100n，原则3：省略最高阶系数：n，记作T(n)=O(n)
T(n)=10n² + 100n，不满足原则1，原则2：最高阶为10n²，原则3：省略最高阶系数：n，记作T(n)=O(n²)
T(n)=1, 仅满足原则1，记作T(n)=O(1)

常见复杂度的大小关系

纯粹的递归复杂度为O(n)
O(1) < O(logn) < O(n) < O(nlogn) < O(n²)等

复杂度的意义

算法A的的执行次数是T(n)=10000n，时间复杂度是O(n)
算法B的的执行次数是T(n)=5n²，时间复杂度是O(n²)
假如A和B分别运行在老旧的计算机和超级计算机上，他们的运行次数如下：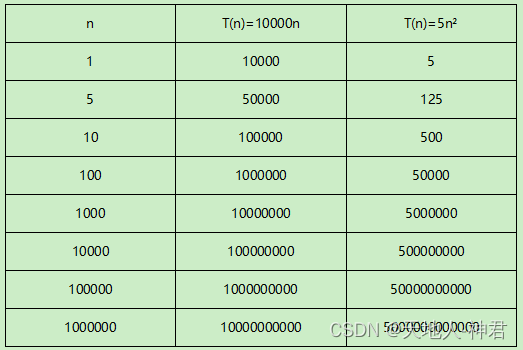

可见，复杂度对衡量算法多么地重要！！！

时间和空间的取舍

大部分时间是舍弃空间换取时间