• Day18：初识B、B+树＆RB树

    一、B树和B+树

    1.B树：


        23树的基础上  引入  M值
        23树就是M值为3的B树

    Day13：数据结构之2-3树__https://blog.csdn.net/zjjaibc/article/details/126194415?spm=1001.2014.3001.5501

    2.B+树：


        B树加上两个特性：
            1. 数据只存在叶子节点上
            2. 叶子节点之间用指针连接


            通常用于数据库和操作系统的文件系统中。B+树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树元素自底向上插入，这与二叉树恰好相反。

            数据库  DB  DBA   关系型数据库  B+树
                MySql  

            硬盘：
                物理结构       (内存四区：代码区  栈区  堆区  静态区
                数据存储结构      B+树  

     查询的时候,

            相当于根据索引大致确定了查找的区间,所有的真实数据均放在叶子结点上,

            且相互连接构成了一个链表,.

    二、红黑树： 

    红黑二叉树：
        不怎么降低AVL的查找效率，大幅优化增删效率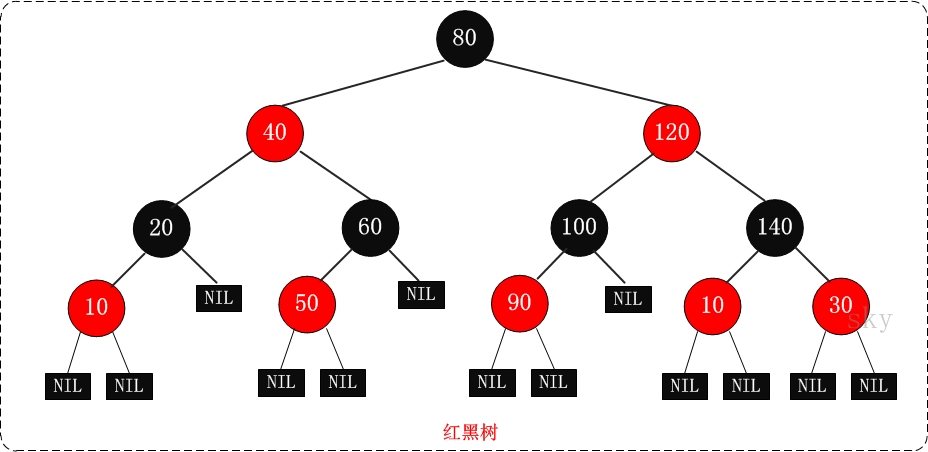

    红黑二叉树 相对AVL树：
        稍稍降低查找效率（不是绝对平衡） 增删效率加快很多（三次旋转搞定）

    红黑二叉树规则：
        1. 树中节点 非红即黑
        2. 根和叶子都是黑节点(空节点算叶子),枝干非红即黑
        3. 红色节点的孩子必定是黑色,插入的结点一开始必为红色,两个红色结点不能相连
        4. 从一个节点到这个节点的任意一个子孙节点路径上包含相同个数的黑色节点。

    红黑二叉树插入步骤：    

    1. 新节点统一着色为红色
        情况一：新节点为根节点
            着色为黑
        情况二：新节点的父节点颜色为黑
            啥都不干
        情况三：新节点的父节点颜色为红色
            3.1 被插入节点父节点颜色为红色，并且叔叔节点颜色为黑色，并且被插入节点是其父节点的左孩子
                3.1.1 父节点设置为黑色
                3.1.2 爷爷节点设置为红色
                3.1.3 以其父节点为轴右旋
            3.2 被插入节点父节点颜色为红色，并且叔叔节点颜色为黑色，并且被插入节点是其父节点的右孩子
                3.2.1 以其父节点为轴 ，左旋
                3.2.2 新节点设置为黑色
            3.3 被插入节点父节点颜色为红色，并且叔叔节点颜色为红色
                3.3.1 父节点设置为黑色
                3.3.2 叔叔节点设置为黑色
                3.3.3 爷爷节点设置为红色
                3.3.4 把爷爷节点当成新节点插入

    (1) 情景1：红黑树为空树

    • 将插入节点作为根节点，然后将根节点设置为黑色

    (2) 情景2：插入点的key已存在

    • 替换原节点的value值

    (3) 情景3：插入节点的父节点是黑节点

    • 直接插入，不会影响自平衡

    (4) 情景4：插入节点的父节点是红节点

    根据性质2：父节点为红色一定不是根节点；根据性质4：爷节点肯定是黑色。

             情景4.1：叔叔节点存在，且为红色

             

    • 将父节点P和叔节点U改为黑色

    • 爷节点PP改为红色。

    • 进行后续处理: 

          情景4.2：叔节点不存在或为黑节点，且插入节点的父节点是爷节点的左孩子  

                    注意：叔叔节点应该非红即空，否则破坏性质

                     情景4.2.1：插入节点是父节点的左孩子（LL双红情况）

    • 将父节点P设为黑色，将爷节点PP设为红色

    • 对爷节点PP进行右旋

                    情景4.2.1：插入节点是父节点的右孩子（LR双红情况）

    • 对父节点P进行左旋

    • 将P设为当前节点，得到LL双红情况

    • 将I设为黑色，将爷节点PP设为红色

    • 对爷节点PP进行右旋

            情景4.3：叔叔节点不存在或为黑节点，且插入节点的父节点是爷节点的右孩子

                    对应情景4.2，只是方向相反

    红黑树代码实现

    1. #include 
    2. #include 			
    3. //辅助宏
    4. #define RED		0
    5. #define BLACK	1
    6. //获取节点的颜色
    7. #define COLOR(x)  ((x)->color)
    8. //获取当前节点的父节点
    9. #define PARENTNODE(x) ((x)->parentNode)
    10. //设置当前节点的父节点
    11. #define SET_PARENT(x,p) ((x)->parentNode=(p))
    12. //设置当前节点的颜色
    13. #define SET_COLOR(x,c) ((x)->color=(c))
    14. //设置当前节点颜色为黑色
    15. #define SET_BLACK(x) ((x)->color=BLACK)
    16. //设置当前节点颜色为红色
    17. #define SET_RED(x) ((x)->color=RED)
    18. //判断当前节点颜色是否为黑色
    19. #define IS_BLACK(x) ((x)->color==BLACK)
    20. //判断当前节点颜色是否为红色
    21. #define IS_RED(x) ((x)->color==RED)
    22. //红黑树的结构体
    23. struct RBTreeNode 
    24. {
    25. 	unsigned int color;			//颜色
    26. 	int key;				//关键字
    27. 	struct RBTreeNode* LChild;
    28. 	struct RBTreeNode* RChild;
    29. 	struct RBTreeNode* parentNode;
    30. }
    31. typedef  struct RBTreeNode	NODE;
    32. typedef  struct RBTreeNode* LPNODE;
    33.  
    34. struct RBTree 
    35. {
    36. 	LPNODE 	root;
    37. 	int 	treeSize;
    38. }
    39. typedef struct RBTree	RBTREE;
    40. typedef struct RBTree*	LPRBTREE;
    41.  
    42. LPNODE createNode(int key) 
    43. {
    44. 	LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
    45. 	newNode->key = key;
    46. 	newNode->LChild = NULL;
    47. 	newNode->RChild = NULL;
    48. 	newNode->parentNode = NULL;
    49. 	newNode->color = BLACK;
    50. 	return newNode;
    51. }
    52. //创建树
    53. LPRBTREE createRBTree() 
    54. {
    55. 	LPRBTREE tree = (LPRBTREE)malloc(sizeof(RBTREE));
    56. 	tree->root = NULL;
    57. 	return tree;
    58. }
    59. //左旋
    60. void L_Rotation(LPRBTREE tree,LPNODE x) 
    61. {
    62. 	//1.拿到x的右边 y怎么表示？
    63. 	LPNODE y = x->RChild;
    64. 	//2.y的左边成为x的右边
    65. 	x->RChild = y->LChild;
    66. 	//3.判断下y的左边是不是空的
    67. 	//父节点的处理
    68. 	if (y->LChild != NULL) {
    69. 		y->LChild->parentNode = x;
    70. 	}
    71. 	//y替换了x ,所以x的父节点就是y的父节点
    72. 	y->parentNode = x->parentNode;
    73. 	//如果x是根不，循环后，红黑树的根改变
    74. 	if (x->parentNode == NULL) {
    75. 		tree->root = y;
    76. 	}
    77. 	else {
    78. 		//不是根部判断x是在原来父节点左边还是右边
    79. 		if(x->parentNode->LChild==x){
    80. 			x->parentNode->LChild = y;
    81. 		}
    82. 		else {
    83. 			x->parentNode->RChild = y;
    84. 		}
    85. 	}
    86. 	//处理一下x的位置
    87. 	y->LChild = x;
    88. 	x->parentNode = y;
    89. }
    90. //右旋
    91. void R_Rotation(LPRBTREE tree, LPNODE y) 
    92. {
    93. 	//拿到x节点
    94. 	LPNODE x = y->LChild;
    95. 	y->LChild = x->RChild;
    96. 	if (x->RChild != NULL) 
    97. 	{
    98. 		x->RChild->parentNode = y;
    99. 	}
    100. 	//处理x和y的父节点
    101. 	x->parentNode = y->parentNode;
    102. 	if (y->parentNode == NULL) 
    103. 	{
    104. 		tree->root = x;
    105. 	}
    106. 	else 
    107. 	{
    108. 		if (y == y->parentNode->LChild) 
    109. 		{
    110. 			y->parentNode->LChild = x;
    111. 		}
    112. 		else 
    113. 		{
    114. 			y->parentNode->RChild = x;
    115. 		}
    116. 	}
    117. 	//
    118. 	x->RChild = y;
    119. 	y->parentNode = x;
    120. }
    121. //1.插入
    122. //1.1 当作BST(有序二叉树)做一个插入
    123. //1.2 调整成为红黑树
    124. void insertAdjustTree(LPRBTREE tree, LPNODE node) 
    125. {
    126. 	LPNODE parent, gparent;
    127. 	while ((parent = PARENTNODE(node)) && IS_RED(parent)) 
    128. 	{
    129. 		gparent = PARENTNODE(parent);
    130. 		//三种情况分析
    131. 		if (parent == gparent->LChild) 
    132. 		{//父节点是祖父节点的左孩子
    133. 			//No.1 U=RED;//对应笔记中的情况三 . 3
    134. 			{
    135. 				LPNODE uncle = gparent->RChild;
    136. 				if (uncle && IS_RED(uncle)) 
    137. 				{
    138. 					SET_BLACK(uncle);		 //uncle->color=BLACK;
    139. 					SET_BLACK(parent);		 //parent->color=BLACK;
    140. 					SET_RED(gparent);	     //gpranet->color=RED;
    141. 					node = gparent;			
    142. 					continue;
    143. 				}
    144. 			}
    145. 			//No.2 u=BLACK S=R //对应笔记中 情况三.1
    146. 			if (parent->RChild == node) 
    147. 			{
    148. 				LPNODE temp;
    149. 				L_Rotation(tree, parent);
    150. 				temp = parent;
    151. 				parent = node;
    152. 				node = temp;
    153. 			}
    154. 			//No.3 U=BLACK S=L    //对应笔记中 情况三.2
    155. 			SET_BLACK(parent);
    156. 			SET_RED(gparent);
    157. 			R_Rotation(tree, gparent);
    158. 		}
    159. 		else 
    160. 		{//父节点是祖父节点的右孩子
    161. 			//No.1   //对应笔记中的情况三 . 3
    162. 			{
    163. 				LPNODE uncle = gparent->LChild;
    164. 				if (uncle && IS_RED(uncle)) 
    165. 				{
    166. 					SET_BLACK(uncle);		 //uncle->color=BLACK;
    167. 					SET_BLACK(parent);		 //parent->color=BLACK;
    168. 					SET_RED(gparent);	     //gpranet->color=RED;
    169. 					node = gparent;
    170. 					continue;
    171. 				}
    172. 			}
    173. 			//No.2  
    174. 			if (parent->LChild == node) //对应笔记中 情况三.1
    175. 			{
    176. 				LPNODE temp;
    177. 				R_Rotation(tree, parent);
    178. 				temp = parent;
    179. 				parent = node;
    180. 				node = temp;
    181. 			}
    182. 			SET_BLACK(parent);//对应笔记中 情况三.2
    183. 			SET_RED(gparent);
    184. 			L_Rotation(tree, gparent);
    185. 		}
    186. 	}
    187. 	SET_BLACK(tree->root);// 对应笔记中 情况一：新节点是根节点
    188. }
    189. //1.1 当作BST做一个插入
    190. void insertNode(LPRBTREE tree, LPNODE node) 
    191. {
    192. 	//当作BST做一个插入
    193. 	LPNODE y = NULL;
    194. 	LPNODE x = tree->root;
    195. 	while (x != NULL) 
    196. 	{
    197. 		y = x;		//记录父节点
    198. 		if (node->key < x->key) 
    199. 		{
    200. 			x = x->LChild;
    201. 		}
    202. 		else 
    203. 		{
    204. 			x = x->RChild;
    205. 		}
    206. 	}
    207. 	//新节点应该插在y节点的下面
    208. 	SET_PARENT(node, y);
    209. 	if (y != NULL) 
    210. 	{
    211. 		if (node->key < y->key) 
    212. 		{
    213. 			y->LChild = node;
    214. 		}
    215. 		else 
    216. 		{
    217. 			y->RChild = node;
    218. 		}
    219. 	}
    220. 	else	//树是空的，第一次插入节点就要成为根节点
    221. 	{
    222. 		tree->root = node;
    223. 	}
    224. 	SET_COLOR(node, RED);		//插入节点着色红色
    225. 	//2.按照红黑树的规则情况去调整二叉树成为红黑树
    226. 	insertAdjustTree(tree, node);
    227. }
    228. void printCurNode(LPNODE curNode) 
    229. {
    230. 	printf("%d:%s\n", curNode->key, curNode->color ? "BLACK" : "RED");
    231. }
    232. void preOrder(LPNODE root) 
    233. {
    234. 	if (root != NULL) 
    235. 	{
    236. 		printCurNode(root);	//printf("%d:%s\n", curNode->key, curNode->color ? "BLACK" : "RED");
    237. 		preOrder(root->LChild);
    238. 		preOrder(root->RChild);
    239. 	}
    240. }
    241. //2.红黑树的删除
    242. //2.1 当做BST 去做删除
    243. //2.2 调整
    244. void deleteAdjustTree(LPRBTREE tree, LPNODE node, LPNODE parent) 
    245. {
    246. 	LPNODE other;
    247. 	while (!node || IS_BLACK(node) && node != tree->root) 
    248. 	{
    249. 		if (parent->LChild == node) //node是其父节点的左孩子
    250. 		{
    251. 			other = parent->RChild;
    252. 			if (IS_RED(other))//node的兄弟为红色节点
    253. 			{
    254. 				//No.1 xB=RED
    255. 				SET_BLACK(other);
    256. 				SET_RED(parent);
    257. 				L_Rotation(tree, parent);
    258. 				other = parent->RChild;
    259. 			}
    260. 			if ((!other->LChild) || IS_BLACK(other->LChild) &&
    261. 				(!other->RChild) || IS_BLACK(other->RChild)) 
    262. 			{
    263. 				//No.2  xB=BLACK
    264. 				SET_RED(other);
    265. 				node = parent;
    266. 				parent = PARENTNODE(node);
    267. 			}
    268. 			else 
    269. 			{
    270. 				if (!other->RChild || IS_BLACK(other->RChild)) 
    271. 				{
    272. 					//No.3 xB=BLACK xB->LChild=RED, xB->RChild=BLACK;
    273. 					SET_BLACK(other->LChild);
    274. 					SET_RED(other);
    275. 					R_Rotation(tree, other);
    276. 					other = parent->RChild;
    277. 				}
    278. 				//No.4 xB=BLACK xB=RChild=RED
    279. 				SET_COLOR(other, COLOR(parent));
    280. 				SET_BLACK(parent);
    281. 				SET_BLACK(other->RChild);
    282. 				L_Rotation(tree, parent);
    283. 				node = tree->root;
    284. 				break;
    285. 			}
    286. 		}
    287. 		else //node是其父节点的右孩子
    288. 		{
    289. 			other = parent->LChild;
    290. 			if (IS_RED(other))
    291. 			{
    292. 				//No.1 xB=RED
    293. 				SET_BLACK(other);
    294. 				SET_RED(parent);
    295. 				L_Rotation(tree, parent);
    296. 				other = parent->LChild;
    297. 			}
    298. 			if ((!other->LChild) || IS_BLACK(other->LChild) &&
    299. 				(!other->RChild) || IS_BLACK(other->RChild))
    300. 			{
    301. 				//No.2  xB=BLACK
    302. 				SET_RED(other);
    303. 				node = parent;
    304. 				parent = PARENTNODE(node);
    305. 			}
    306. 			else
    307. 			{
    308. 				if (!other->LChild || IS_BLACK(other->LChild))
    309. 				{
    310. 					//No.3 xB=BLACK xB->RChild=RED, xB->LChild=BLACK;
    311. 					SET_BLACK(other->RChild);
    312. 					SET_RED(other);
    313. 					L_Rotation(tree, other);
    314. 					other = parent->LChild;
    315. 				}
    316. 				//No.4 xB=BLACK xB=LChild=RED
    317. 				SET_COLOR(other, COLOR(parent));
    318. 				SET_BLACK(parent);
    319. 				SET_BLACK(other->LChild);
    320. 				R_Rotation(tree, parent);
    321. 				node = tree->root;
    322. 				break;
    323. 			}
    324. 		}
    325. 	}
    326. 	if (node) 
    327. 	{
    328. 		SET_BLACK(node);
    329. 	}
    330. }
    331. //2.1 当做BST 去做删除
    332. void deleteNode(LPRBTREE tree, LPNODE node) 
    333. {
    334. 	LPNODE child, parent;
    335. 	int color;					//删除节点兄弟的颜色
    336. 	//左右子树都存在
    337. 	if ((node->LChild) != NULL && (node->RChild) != NULL)
    338. 	{
    339. 		LPNODE replace = node;
    340. 		replace = replace->RChild;		//调整树：从右子树中拿最左边
    341. 		while (replace->LChild != NULL)
    342. 		{
    343. 			replace = replace->LChild;
    344. 		}
    345. 		//讨论删除节点是不是根节点
    346. 		if (PARENTNODE(node))
    347. 		{
    348. 			if (PARENTNODE(node)->LChild == node)
    349. 			{
    350. 				PARENTNODE(node)->LChild = replace;
    351. 			}
    352. 			else
    353. 			{
    354. 				PARENTNODE(node)->RChild = replace;
    355. 			}
    356. 		}
    357. 		else 
    358. 		{
    359. 			tree->root = replace;
    360. 		}
    361. 		child = replace->RChild;
    362. 		parent = PARENTNODE(replace);
    363. 		color = COLOR(replace);
    364. 		if (parent == node) 
    365. 		{
    366. 			parent = replace;
    367. 		}
    368. 		else 
    369. 		{
    370. 			if (child) 
    371. 			{
    372. 				SET_PARENT(child, parent);
    373. 			}
    374. 			parent->LChild = child;
    375. 			replace->RChild = node->RChild;
    376. 			SET_PARENT(node->RChild, replace);
    377. 		}
    378. 		//调整替换节点父节点
    379. 		replace->parentNode = node->parentNode;
    380. 		replace->color = node->color;
    381. 		replace->LChild = node->LChild;
    382. 		//调整删除节点父节点
    383. 		node->LChild->parentNode = replace;
    384. 		if (color == BLACK) 
    385. 		{
    386. 			//调整树：
    387. 			deleteAdjustTree(tree, child, parent);
    388. 		}
    389. 		free(node);
    390. 		return;
    391. 	}
    392. 	if (node->LChild != NULL) 
    393. 	{
    394. 		child = node->LChild;
    395. 	}
    396. 	else 
    397. 	{
    398. 		child = node->RChild;
    399. 	}
    400. 	parent = node->parentNode;
    401. 	color = node->color;
    402. 	if (parent) 
    403. 	{
    404. 		if (parent->LChild == node) 
    405. 		{
    406. 			parent->LChild = child;
    407. 		}
    408. 		else 
    409. 		{
    410. 			parent->RChild = child;
    411. 		}
    412. 	}
    413. 	else
    414. 	{
    415. 		tree->root = child;
    416. 	}
    417. 	if (color == BLACK) 
    418. 	{
    419. 		//调整二叉树
    420. 		deleteAdjustTree(tree, child, parent);
    421. 	}
    422. 	free(node);
    423. }
    424. LPNODE search(LPNODE x, int key)
    425. {
    426. 	if (x == NULL || x->key == key)
    427. 		return x;
    428. 	if (key < x->key) 
    429. 	{
    430. 		return search(x->LChild, key);
    431. 	}
    432. 	else 
    433. 	{
    434. 		return search(x->RChild, key);
    435. 	}
    436. }
    437. void deleteTreeNode(LPRBTREE tree, int key) 
    438. {
    439. 	LPNODE result = search(tree->root, key);
    440. 	if (result != NULL)
    441. 		deleteNode(tree, result);
    442. }
    443.  
    444. int main()
    445. {
    446. 	int array[] = {10,40,30,60,90,70,20,50,80};
    447. 	int arrayNum = 9;
    448. 	LPRBTREE tree = createRBTree();
    449. 	for (int i = 0; i < arrayNum; i++) 
    450. 	{
    451. 		insertNode(tree, createNode(array[i]));
    452. 	}
    453. 	preOrder(tree->root);
    454. 	printf("\n");
    455. 	printf("删除:\n");
    456. 	deleteTreeNode(tree, 10);
    457. 	preOrder(tree->root);
    458. 	printf("\n");
    459. 	printf("删除:\n");
    460. 	deleteTreeNode(tree, 80);
    461. 	preOrder(tree->root);
    462. 	printf("\n");
    463.  
    464. 	while(1);//防止闪屏
    465. 	return 0;
    466. }

  • 相关阅读:
    Ubuntu下载、安装QGIS软件的方法
    使用python生成文字图片，画圆圈 ，生成圆形图片
    前端多环境部署
    IntelliJ IDEA 2023.1 版本可以安装了
    STM32F1读取MLX90632非接触式红外温度传感器
    MyBatis——表的关联关系,事务，ORM，缓存机制
    ESP32网络开发实例-Web服务器控制GPIO
    猿创征文 |《深入浅出Vue.js》打卡Day6
    HoG（梯度直方图）原理及python实现
    Java虚拟机二三事：虚拟机类加载机制
  • 原文地址：https://blog.csdn.net/zjjaibc/article/details/126399611