Python数据分析案例02——泰尔指数的计算

泰尔指数是在经济学管理学中写论文常见的一种评价发展是否平衡的一种方法。适用于面板数据，基本思想是利用每个地区的人均收入和总人口数进行加权计算，比较一个地区的不同地方发展是否平衡，类似于方差分析。就是研究分类型自变量对数值型因变量的影响，只不过加了个权用指数表示出来了。

具体公式和计算原理介绍如下：

---

泰尔指数计算：

总差异的Theil指数公式如下:

本文中的区域表示的是城市和农村两大区域，分组是分成了31个省份。
也就是说，这里的区域之间就是农村跟城市之间，城市之间就是每个省份之间。

---

看不懂没关系....下面直接看代码。需要这代码演示数据的同学可以参考：数据

---

导入包：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
#import seaborn as sns
plt.rcParams ['font.sans-serif'] ='SimHei'            
plt.rcParams ['axes.unicode_minus']=False     

读取数据：观察数据的样子

data=pd.read_excel('2000-2019年分地区人均可支配收入、城市和农村可支配收入以及泰尔指数.xlsx')
data.head()

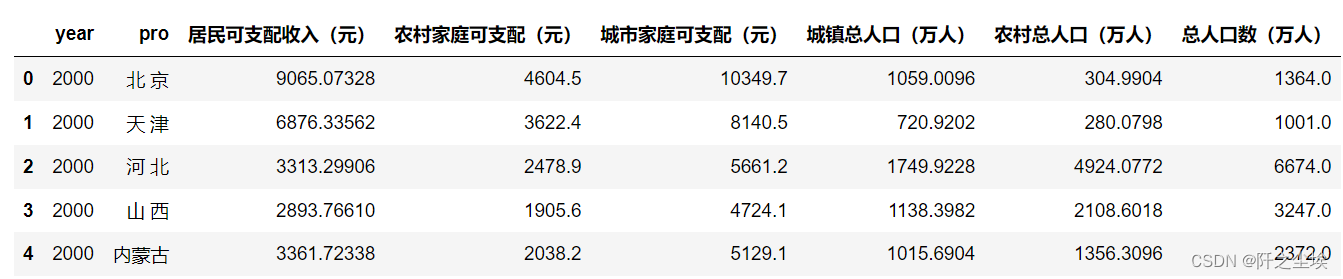
 典型的面板数据，有时间和地区两个变量。

首先我们计算农村的泰尔指数，先通过数据透视表或者分组聚合方法得到每个地区每年的单独的数据：

农村平均家庭可支配=data.groupby(['year','pro'])['农村家庭可支配（元）'].mean().unstack()
农村总人口=data.groupby(['year','pro'])['农村总人口（万人）'].mean().unstack()
#还可以像下面这样数据透视，结果也是一样的
农村平均家庭可支配=data.pivot(index='year',columns='pro',values='农村家庭可支配（元）')
农村总人口=data.pivot(index='year',columns='pro',values='农村总人口（万人）')

查看数据前5行

农村平均家庭可支配.head()

31个省份各自的农村家庭平均收入，农村总人口也是一样的，不展示了。

下面将农村家庭平均收入乘上农村总人口，可以得到每个省份每年的农村总可支配收入：

农村家庭可支配=农村总人口*农村平均家庭可支配
农村家庭可支配.head()

 然后对省份进行求和，相对于对列求和，计算每年所有省份的农村家庭可支配收入的总和：

农村家庭可支配.sum(axis=1)

 然后按时间上，也是每行上，每个省份都除以当前年份的这个总和数。

人口也是做同样的处理，每年所有省份求和，然后再分别除以这个求和数。

就相对于计算了每年每个省份各自的农村可支配收入的比例，然后除以人口的这个比例，然后取对数。

农村家庭可支配=农村家庭可支配.div(农村家庭可支配.sum(axis=1),axis=0)
农村总人口=农村总人口.div(农村总人口.sum(axis=1),axis=0)
农村家庭可支配2=农村家庭可支配.copy()
农村家庭可支配=农村家庭可支配/农村总人口
 
for i in 农村家庭可支配.columns:
    农村家庭可支配[i]= 农村家庭可支配[i].apply(np.log) 

我这里变量名有点乱，都把前面的覆盖了....

计算出来的对数后和原来的农村家庭可支配比例相乘，然后按列求和，也就是对每各省份求和，然后除以省份个数31，就可以得到我们的农村泰尔指数。

农村家庭可支配=农村家庭可支配*农村家庭可支配2
农村家庭可支配['logsum']= 农村家庭可支配.sum(axis=1)/31
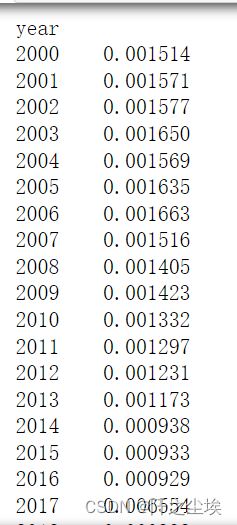
农村泰尔指数=农村家庭可支配['logsum']
农村泰尔指数

---

下面再计算城市泰尔指，流程就和上面一样了

城市家庭可支配=data.groupby(['year','pro'])['城市家庭可支配（元）'].mean().unstack()
城市总人口=data.groupby(['year','pro'])['城镇总人口（万人）'].mean().unstack()
城市家庭可支配=城市总人口*城市家庭可支配
城市家庭可支配=城市家庭可支配.div(城市家庭可支配.sum(axis=1),axis=0)
城市总人口=城市总人口.div(城市总人口.sum(axis=1),axis=0)
城市家庭可支配2=城市家庭可支配.copy()
城市家庭可支配=城市家庭可支配/城市总人口
for i in 城市家庭可支配.columns:
    城市家庭可支配[i]= 城市家庭可支配[i].apply(np.log) 
    
城市家庭可支配=城市家庭可支配*城市家庭可支配2
城市家庭可支配['logsum']= 城市家庭可支配.sum(axis=1)/31
城市泰尔指数=城市家庭可支配['logsum']

查看

城市泰尔指数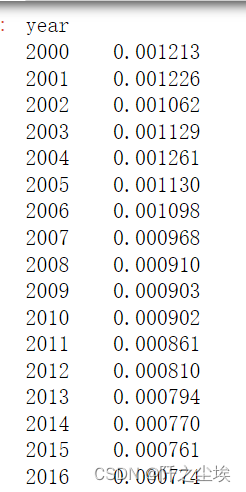

---

再计算总体的城乡间的泰尔指数

总体家庭可支配=data.groupby(['year','pro'])['居民可支配收入（元）'].mean().unstack()
总体总人口=data.groupby(['year','pro'])['总人口数（万人）'].mean().unstack()
 
总体家庭可支配=总体总人口*总体家庭可支配
总体家庭可支配=总体家庭可支配.div(总体家庭可支配.sum(axis=1),axis=0)
总体总人口=总体总人口.div(总体总人口.sum(axis=1),axis=0)
总体家庭可支配2=总体家庭可支配.copy()
 
总体家庭可支配=总体家庭可支配/总体总人口
for i in 总体家庭可支配.columns:
    总体家庭可支配[i]= 总体家庭可支配[i].apply(np.log) 
    
总体家庭可支配=总体家庭可支配*总体家庭可支配2
总体家庭可支配['logsum']= 总体家庭可支配.sum(axis=1)/31
城乡间泰尔指数=总体家庭可支配['logsum']
城乡间泰尔指数

---

将结果写到一个数据框里面，然后求和，计算各自的比例，储存

df=pd.DataFrame()
df['农村泰尔指数']=农村泰尔指数
df['城市泰尔指数']=城市泰尔指数
df['城乡间泰尔指数']=城乡间泰尔指数
df['总泰尔指数']=df.sum(axis=1)  #求和

计算比例

df['农村贡献率(%)']=df['农村泰尔指数']/df['总泰尔指数']
df['城市贡献率(%)']=df['城市泰尔指数']/df['总泰尔指数']
df['城乡间贡献率(%)']=df['城乡间泰尔指数']/df['总泰尔指数']

文本索引

df.index=[str(i) for i in df.index]

储存

df.to_excel('结果.xlsx')

---

结果可视化

df[['农村泰尔指数','城市泰尔指数','城乡间泰尔指数','总泰尔指数']].plot(figsize=(14,6),title='2000-2019 年居民收入泰尔指数走势图')
plt.savefig('2000-2019 年居民收入泰尔指数走势图.jpg',dpi=256)

比例的可视化

df[['农村贡献率(%)','城市贡献率(%)','城乡间贡献率(%)']].plot(figsize=(14,6),title='2000-2019 年农村、城市、城乡间泰尔指数对总泰尔指数的贡献率')
plt.savefig('2000-2019 年农村、城市、城乡间泰尔指数对总泰尔指数的贡献率图.jpg',dpi=256)

 

 分析：

我们通过的泰尔指数走势图会发现，从2000年到2019年泰尔指数整体趋势，无论是农村还是城市，都是在下降。说明发展不平衡的现象有所缓解。

从农村城市城乡间泰尔指数最总泰尔指数的贡献率来看，城乡之间的泰尔指数对总泰尔指数的贡献率最大，说明城乡之间的收入差距较大，农村的贡献率一直大于城市间贡献率说明，各省份农村之间的收入差异比起城市也较大。

（进一步还可以分析几几年在下降，下降的快和慢等等，最近几年较为平缓，城乡见贡献度有下降趋势等等）

创作不易，看官觉得写得还不错的话点个关注和赞吧，本人会持续更新python数据分析领域的代码文章~(需要定制代码可私信)