【二叉树】链式结构的一些操作实现

前言

二叉树的定义及数的概念在上一篇文章–>【二叉树】数中的特殊结构-＞堆
本章直接进入二叉树的实现及一些二叉树的操作实现

---

✨目录

1. 二叉树链式结构的实现
2. 二叉树的遍历
3. 节点个数以及高度等

---

1.二叉树链式结构的实现

---

再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树
2. 非空：根节点，根节点的左子树、根节点的右子树组成的

从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的

二叉树的链式结构在代码中的定义

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;//数据域
	struct BinaryTreeNode* left;//左孩子
	struct BinaryTreeNode* right;//右孩子
}BTNode;
1
2
3
4
5
6
7

2.二叉树的遍历

---

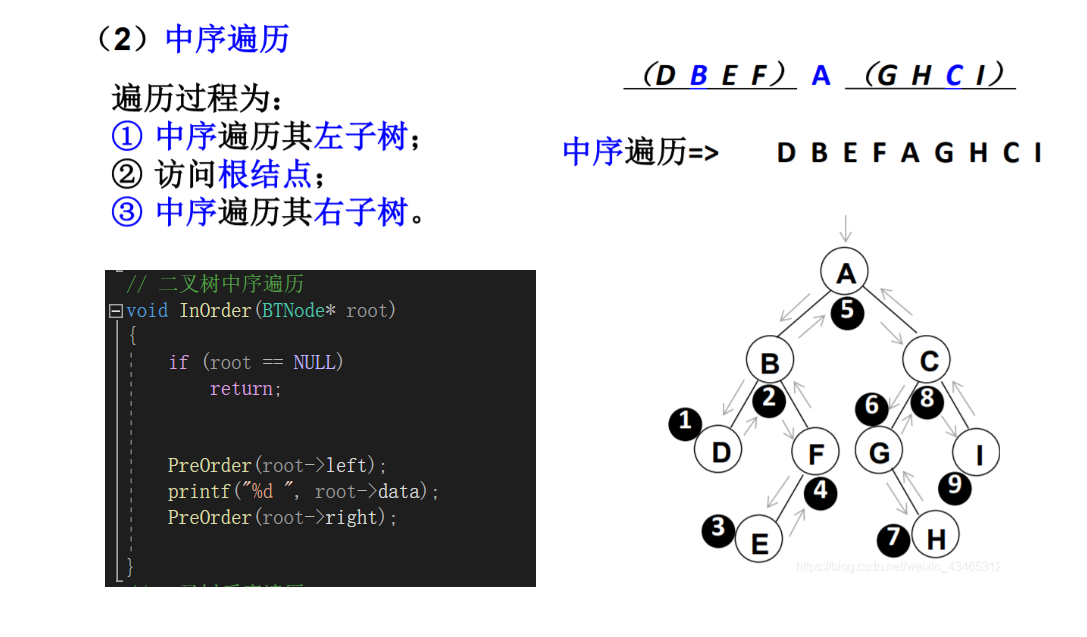
2.1 前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉
树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历
是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为
根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

// 二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
		return;

	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
		return;


	PreOrder(root->left);
	printf("%d ", root->data);
	PreOrder(root->right);
	
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
		return;


	PreOrder(root->left);
	PreOrder(root->right);
	printf("%d ", root->data);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

下面主要分析前序递归遍历，中序与后序图解类似，各位可自己动手绘制。

• 后序遍历也是类似

2.2 层序遍历

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层
上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

//二叉树层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL)
		return;
	//层序遍历需要队列，C语言要自行实现
	//Queue q;  定义一个队列
	//QueueInit(&q);队列初始化
	//QueuePush(&q, root);把数中第一个元素入队列
	while (!QueueEmpty(&q))//队列不为空则继续
	{

		BTNode cur = QueueFront(&q);//取队列元素，随带把取出来的元素中的左右子树依次入队列
		if (cur.left != NULL)
			QueuePush(&q, cur.left);
		if (cur.left != NULL)
			QueuePush(&q, cur.right);
		QueuePop(&q);
		if (&cur != NULL)
			printf("%c ", cur.data);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

3.节点个数以及高度等

---

二叉树的节点个数

int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
1
2
3
4
5
6
7

二叉树高度

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftdepth = BinaryTreeSize(root->left);
	int rightdepth = BinaryTreeSize(root->right);

	return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}
1
2
3
4
5
6
7
8
9
10

二叉树的叶子节点

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right == NULL)//左右子树为空即为叶子节点
		return 1;

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);

}
1
2
3
4
5
6
7
8
9
10
11
12

二叉树的销毁

//二叉树销毁类似后序遍历
void BinaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
		return;

	BinaryTreeDestory(&(*root)->left);
	BinaryTreeDestory(&(*root)->right);
	free(*root);
	*root = NULL;
}
1
2
3
4
5
6
7
8
9
10
11

二叉树的前序构建

//给定一个前序遍历数节点的数组即可构建一颗二叉树
//例如：abc##de#g##f###  “#”代表空（NULL）

/*
  a->数组地址
  pi-> 首元素下标
*/
BTNode* BinaryTreeCreate(BTDataType* a,  int* pi)
{
	if (a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->data = a[*pi];
	(*pi)++;
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);
	return root;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23