【数模系列】03_层次分析法

😃：本篇博客参考B站清风

一、层次分析法

层次分析法（The analytic hierarchy process，简称AHP）

是建模比赛中最基础的模型之一，其主要用于解决评价类问题(例如:选择哪种方案最好、哪位运动员或者员工表现的更优秀)。

1、解决评价类问题

评价类问题可以用打分来解决：

例子：小明选大学
小明最关心大学里面的这四个方面：
1、学习氛围(0.4)
2、就业前景(0.3)
3、男女比例(0.2)
4、校园景色(0.1)
其中，括号里面的数值表示小明认为的重要性程度（权重)，其和为1。

A校最终得分：0.515=0.7 ×0.4＋0.5 ×0.3 ＋0.3 ×0.2+0.25 ×0.1
B校最终得分：0.485=0.3×0.4＋0.5×0.3＋0.7 ×0.2 +0.75 ×0.1

使用打分法解决评价问题，只需要我们补充完成下面这张表格即可：

填好志愿后，小明同学想出去旅游。在查阅了网上的攻略后，他初步选择了苏杭、北戴河和桂林三地之一作为目标景点。请你确定评价指标、形成评价体系来为小明同学选择最佳的方案。

解决评价类问题，首先要想到以下三个问题：
①我们评价的目标是什么?
选择一处目标景点。
②我们为了达到这个目标有哪几种可选的方案?
三种。
③评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
题目没有给相关数据的支撑，需要我们自己确定。

从上述分析可知：前两个问题的答案是显而易见的，第三个问题的答案需要我们根据题目中的背景材料、常识以及网上搜集到的参考资料进行结合，从中筛选出最合适的指标。

【1】确定评价指标

优先选择 知网(或者万方、百度学术、谷歌学术等平台) 搜索相关的文献：

推荐网站：虫部落-快搜

【2】确定指标优先级

优先级：
1、谷歌搜索（国内进不去的话就使用百度搜索吧)
2、微信搜索
3、知乎搜索

例如本题我们可以搜索关键字：旅游选择因素、根据什么因素选择旅游景点、旅游景点评价指标等。

经过查询了资料后选择了以下五个指标：
①景点景色
②旅游花费
③居住球境
④饮食情况
⑤交通便利程度

在确定影响某因素的诸因子在该因素中所占的比重时，遇到的主要困难是这些比重常常不易定量化。此外，当影响某因素的因子较多时，直接考虑各因子对该因素有多大程度的影响时，常常会因考虑不周全、顾此失彼而使决策者提出与他实际认为的重要性程度不相一致的数据，甚至有可能提出一组隐含矛盾的数据。

问题：一次性考虑这五个指标之间的关系，往往考虑不周。
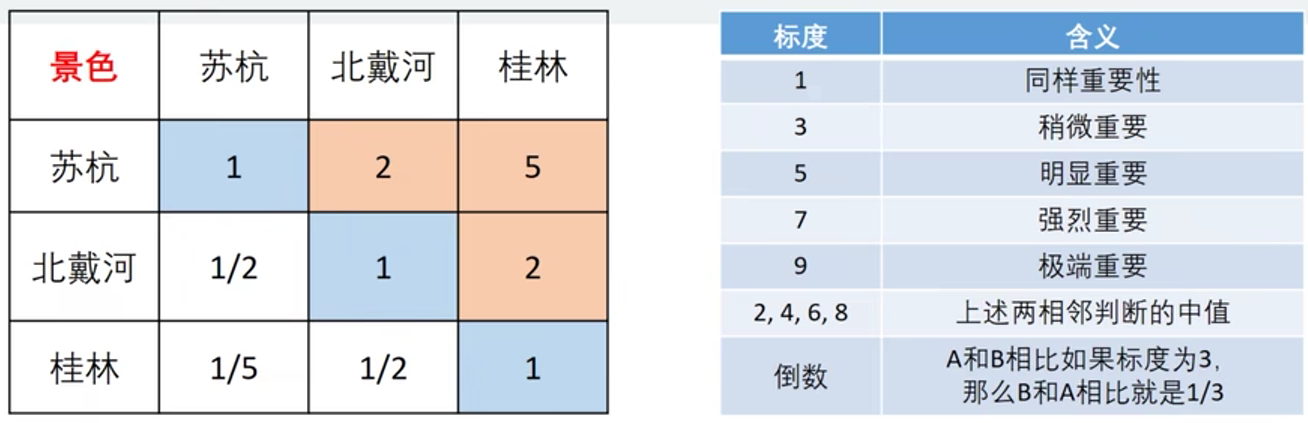
解决方法：两个两个指标进行比较，最终根据两两比较的结果来推算出权重。

如果用1-9表示重要程度（(见下表)，请你两两比较上述这五个指标对最终的旅游景点的重要性：

注：这里的重要性有时解释为满意度

【3】填写判断矩阵

判断矩阵中的元素只能是1至9和它们的倒数。

总结：上面这个表是一个5 $\times$ 5的方针，我们记为A，对应的元素为$a_{ij}$
这个方针有如下特点：
（1）$a_{ij}$表示的意义是，与指标j相比，i的重要程度。
（2）当i=j时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1。
（3）$a_{ij}>0$且满足$a_{ij}$ $\times$ $a_{ji}=1$ （满足这一条件的矩阵为正互反矩阵）

实际上，上面这个矩阵就是层次分析法中的判断矩阵。

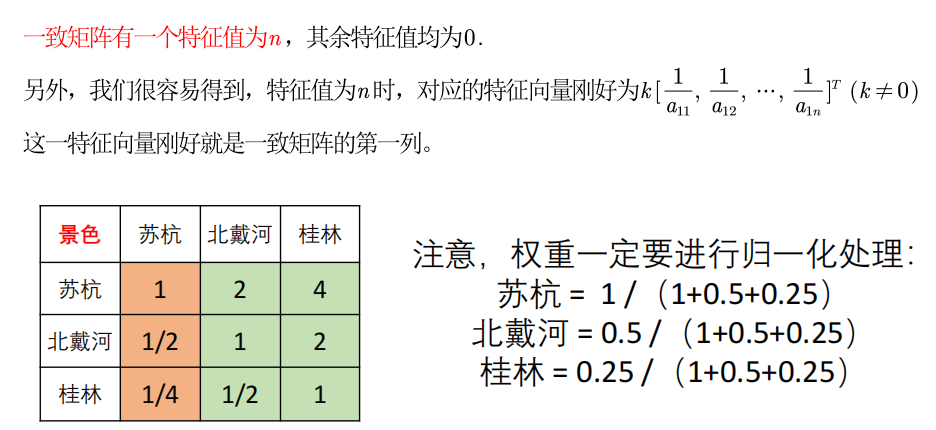
【4】填写一致矩阵

$$a_{ij}=\frac{i的重要程度}{j的重要程度},a_{jk}=\frac{j的重要程度}{k的重要程度}$$
$$a_{ik}=\frac{i的重要程度}{k的重要程度}=a_{ij}\times a_{jk}$$

若矩阵中每个元素aij >0且满足$aij\times aji=1$，则我们称该矩阵为正互反矩阵。在层次分析法中，我们构造的判断矩阵均是正互反矩阵。若正互反矩阵满足$aij\times ajk=aik$，则我们称其为一致矩阵。

一个有可能出现问题的地方：

下图当中的左边就出现了不一致矩阵：

【5】一致性检验

注：
（1）一致矩阵不需要进行一致性检验，只有非一致矩阵的判断矩阵才需要进行一致性检验。
（2）在论文写作中，应该先进行一致性检验，通过检验后再计算权重。

原理：检验我们构造的判断矩阵和一致矩阵是否有太大的差别。

引理: n阶正互反矩阵A为一致矩阵时当且仅当最大特征值 $\lambda max=n$，且当正互反矩阵A非一致时，一定满足$\lambda max>n$

判断矩阵越不一致时，最大特征值与n相差就越大。

一致性检验的步骤：

第一步：计算一致性指标CI
$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

第二步：查找对应的平均随机一致性指标RI

第三步：计算一致性比例CR
$$CR=\frac{CI}{RI}$$

如果CR<0.1，则可认为判断矩阵的一致性可接受，否则需要对判断矩阵进行修正。

【6】求权重

方法一：算术平均法求权重

• 第一步：将判断矩阵按照列归一化（每个元素除以其所在列的和）
  

• 第二步：将归一化的各列相加（按行求和）
  

• 第三步：将相加后得到的向量中每个元素除以n即可得到权重向量
  

方法二：几何平均法求权重

• 第一步：将A的元素按照行相乘得到一个新的列向量
• 第二步：将新的向量的每个分量开n次方
• 第三步：对该列向量进行归一化即可得到权重向量

方法三：特征值法求权重

• 第一步:求出矩阵A的最大特征值以及其对应的特征向量
• 第二步:对求出的特征向量进行归一化即可得到我们的权重

汇总结果得到权重矩阵

使用此矩阵，可以计算每个旅游景点的得分：使用指标权重与对应系数相乘再求和。

【7】层次分析法第一步

1、分析系统中各因素之间的关系，建立系统的递阶层次结构。

旅游地选择层次结构图：

如果用到了层次分析法，那么这个层次结构图要放在你的建模论文中。

【8】层次分析法第二步

对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵)。

【9】层次分析法第三步

由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验(检验通过权重才能用)。

三种方法计算权重：
（1）算术平均法
（2）几何平均法
（3）特征值法

建议大家在比赛时三种方法都使用：
以往的论文利用层次分析法解决实际问题时，都是采用其中某一种方法求权重,而不同的计算方法可能会导致结果有所偏差。为了保证结果的稳健性，本文采用了三种方法分别求出了权重，再根据得到的权重矩阵计算各方案的得分，并进行排序和综合分析，这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效。

【10】层次分析法局限性

(1)评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异可能会很大。

(2)如果决策层中指标的数据是已知的，那么我们如何利用这些数据来使得评价的更加准确呢?

【11】优秀论文的做法

二、代码解释

注意：
在论文写作中，应该先对判断矩阵进行一致性检验，然后再计算权重，因为只有判断矩阵通过了一致性检验，其权重才是有意义的。
在下面的代码中，我们先计算了权重，然后再进行了一致性检验，这是为了顺应计算过程，事实上在逻辑上是说不过去的。
因此大家自己写论文中如果用到了层次分析法，一定要先对判断矩阵进行一致性检验。 而且要说明的是，只有非一致矩阵的判断矩阵才需要进行一致性检验。
如果你的判断矩阵本身就是一个一致矩阵，那么就没有必要进行一致性检验。

1、输入判断矩阵

clear;clc
disp('请输入判断矩阵A： ')
% A = input('判断矩阵A=')
A =[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法，可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 也可以写成多行:
[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
% 两行之间以分号结尾（最后一行的分号可加可不加），同行元素之间以空格（或者逗号）分开。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

补充一种输入矩阵的方法：创建新的变量，命名为AAA-》导入Excel表格的数据-》之后让A=AAA即可。

2、算术平均法求权重

% 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）
Sum_A = sum(A)

[n,n] = size(A)  % 也可以写成n = size(A,1)
% 因为我们的判断矩阵A是一个方阵，所以这里的r和c相同，我们可以就用同一个字母n表示
SUM_A = repmat(Sum_A,n,1)   %repeat matrix的缩写
% 另外一种替代的方法如下：
    SUM_A = [];
    for i = 1:n   %循环哦，这一行后面不能加冒号（和Python不同），这里表示循环n次
        SUM_A = [SUM_A; Sum_A]
    end
clc;A
SUM_A
Stand_A = A ./ SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可

% 第二步：将归一化的各列相加(按行求和)
sum(Stand_A,2)

% 第三步：将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和，得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可（注意这里也可以用./哦）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3、几何平均法求权重

%% 方法2：几何平均法求权重
% 第一步：将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod函数和sum函数类似，一个用于乘，一个用于加  dim = 2 维度是行

% 第二步：将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 这里对每个元素进行乘方操作，因此要加.号哦。  ^符号表示乘方哦  这里是开n次方，所以我们等价求1/n次方

% 第三步：对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
1
2
3
4
5
6
7
8
9
10
11
12
13
14

4、特征值法求权重

% 第一步：求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A)    %V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）
Max_eig = max(max(D)) %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了？ 需要用到find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了，我们要得到最大特征值的位置，就需要将包含所有特征值的这个对角矩阵D中，不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列。

% 第二步：对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量，然后再进行标准化。

%% 计算一致性比例CR
clc
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR < 0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

三、MATLAB基础常识

1、常见符号

(1) 在每一行的语句后面加上分号(一定要是英文的哦;中文的长这个样子；)

加了分号：表示不显示运行结果

a = 3;
a = 5
1
2

（2）多行注释：选中要注释的若干语句,快捷键Ctrl+R

（3）取消注释：选中要取消注释的语句,快捷键Ctrl+T

（4）clear：可以清楚工作区的所有变量

也可以右键删除单个变量。

（5）clc：可以清除命令行窗口中的所有文本,让屏幕变得干净

clear;clc   % 分号也用于区分行。
1

这两条一起使用，起到“初始化”的作用，防止之前的结果对新脚本文件（后缀名是 .m）产生干扰。

（6）按上下键可以调出之前运行的代码

（7）变量
变量在同一行中间用逗号分隔，也可以不用逗号，直接用空格

a = [1,2,3]    
a = [1 2 3]
1
2

（8）矩阵

matlab矩阵有两种写法，可以直接写到一行:

 [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
1

也可以写成多行:

[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
1
2
3
4
5

两行之间以分号结尾（最后一行的分号可加可不加），同行元素之间以空格（或者逗号）分开。

（9）双击工作区的变量可以查看具体细节

（10）新建数据并从Excel表格当中插入

在工作区右键，就可以创建新的变量，并且双击新创建好的变量就可以粘贴Excel表格的数据。

2、输入和输出函数(disp 和 input)

1、 disp函数

matlab中disp()就是屏幕输出函数，类似于c语言中的printf（）函数

disp('我是小温')
1

2、 input函数
input函数如果不加分号，则不会显示运算结果，这点和 disp函数不同，disp函数无论加不加分号都会显示出结果。

一般我们会将输入的数、向量、矩阵、字符串等赋给一个变量，这里我们赋给A：

A = input('请输入A：');
B = input('请输入B：')
1
2

3、两个字符串合并

matlab中两个字符串的合并有两种方法：

（1）strcat(str1,str2……,strn)

 strcat('字符串1','字符串2') 
1

（2）[str 1,str 2，……, str n]或[str1 str2 …… strn]

['字符串1'  '字符串2']
['字符串1','字符串2']
1
2

将字符串放入向量当中，就能自动将字符串进行合并。

4、将数字转换为字符串

字符串函数：num2str ，可以将数字转换为字符串

c = 100
num2str(c) 
disp(['c的取值为' num2str(c)])
disp(strcat('c的取值为', num2str(c)))
1
2
3
4

num2str© ：输出将数字转成成字符串之后的值

5、sum函数

（1）如果是向量（无论是行向量还是列向量），都是直接求和

E = [1,2,3]
sum(E)
E = [1;2;3]
sum(E)
1
2
3
4

（2）如果是矩阵，则需要根据行和列的方向作区分

• a=sum(x)或者a = sum(E,1) 按列求和(得到一个行向量）

• a=sum(x,2); 按行求和(得到一个列向量）

• a=sum(x(:));或者a = sum(sum(E))对整个矩阵求和

6、提取矩阵中指定位置的元素

（1）取指定行和列的一个元素（输出的是一个值）

A(2,1)：得到第二行第一个位置的元素。

A(3,2)：得到第三行第二个位置的元素。

（2）取指定的某一行的全部元素（输出的是一个行向量）

A(2,:) ：去第二行所有元素。

A(5,:) ：取第二列所有元素。

（3）取指定的某一列的全部元素（输出的是一个列向量）

A(:,1) ：取第一列的所有元素

A(:,3) ：取第三列的所有元素

（4）取指定的某些行的全部元素（输出的是一个矩阵）

A([2,5],:) ： 只取第二行和第五行（一共2行）
A(2:5,:) ： 取第二行到第五行（一共4行）
A(2:2:5,:) ：取第二行和第四行 （从2开始，每次递增2个单位，到5结束）
A(2:end,:) ：取第二行到最后一行
A(2:end-1,:) ： 取第二行到倒数第二行

（5）取全部元素(按列拼接的，最终输出的是一个列向量)

7、size函数

clc;
A = [1,2,3;4,5,6]
B = [1,2,3,4,5,6]
size(A)
size(B)
1
2
3
4
5

size(A)函数是用来求矩阵A的大小的,它返回一个行向量，第一个元素是矩阵的行数，第二个元素是矩阵的列数

B矩阵是一行六列。

将矩阵A的行数返回到第一个变量r，将矩阵的列数返回到第二个变量c：

[r,c] = size(A)
r = size(A,1)  %返回行数
c = size(A,2) %返回列数
1
2
3

8、repmat函数

B = repmat(A,m,n)：将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。

A = [1,2,3;4,5,6]
B = repmat(A,2,1)
B = repmat(A,3,2)
1
2
3

9、矩阵当中的运算

（1） 在矩阵的运算中，“”号和“/”号代表矩阵之间的乘法与除法 (A/B = Ainv(B))

A = [1,2;3,4]
B = [1,0;1,1]
A * B
inv(B)  % 求B的逆矩阵
B * inv(B)
A * inv(B)
A / B
1
2
3
4
5
6
7

（2）两个形状相同的矩阵对应元素之间的乘除法需要使用“.*”和“./”

A = [1,2;3,4]
B = [1,0;1,1]
A .* B
A ./ B
1
2
3
4

（3）每个元素同时和常数相乘或相除操作都可以使用

A = [1,2;3,4]
A * 2
A .* 2
A / 2 
A ./ 2
1
2
3
4
5

（4）每个元素同时乘方时只能用 .^

A = [1,2;3,4]
A .^ 2
A ^ 2 
A * A
1
2
3
4

10、求特征值和特征向量

在Matlab中，计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法：

A = [1 2 3 ;2 2 1;2 0 3]
1

（1）E=eig(A)：求矩阵A的全部特征值，构成向量E。

（2）[V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。（V的每一列都是D中与之相同列的特征值的特征向量）

11、find函数的基本用法

find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。

clc;X = [1 0 4 -3 0 0 0 8 6]
ind = find(X)
1
2

其有多种用法，比如返回前2个不为0的元素的位置：

ind = find(X,2)
1

上面针对的是向量（一维），若X是一个矩阵（二维，有行和列），索引该如何返回呢？

假如你需要按照行列的信息输出该怎么办呢？

[r,c] = find(X)
[r,c] = find(X,1) %只找第一个非0元素
1
2

12、矩阵与常数的大小判断运算

共有三种运算符：大于> ;小于< ;等于 == （一个等号表示赋值；两个等号表示判断）

%% 矩阵与常数的大小判断运算
% 共有三种运算符：大于> ;小于< ;等于 ==  （一个等号表示赋值；两个等号表示判断）
clc
X = [1 -3 0;0 0 8;4 0 6]
X > 0
X == 4
1
2
3
4
5
6

13、判断语句

Matlab的判断语句，if所在的行不需要冒号，语句的最后一定要以end结尾 ；中间的语句要注意缩进。