【数据结构】二叉树相关OJ题

一、单值二叉树

题目链接

965. 单值二叉树 - 力扣（LeetCode）

题目描述

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

思路分析

递归解决：先比较根节点和两个子节点的val，如果不相等就返回false，相等就返回true，然后递归比较左子树和右子树。

代码实现

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
        return true;
    if(root->left && root->left->val != root->val)
        return false;
    if(root->right && root->right->val != root->val)
        return false;
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}
1
2
3
4
5
6
7
8
9

---

二、相同的树

题目链接

100. 相同的树 - 力扣（LeetCode）

题目描述

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

思路分析

递归解决：比较两棵树根节点的val是否相同，在递归比较左右子树节点的val是否相同。

代码实现

//思路：检查节点的值或者节点的数量是否相同，如果不同直接返回false，然后递归检查左右子树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)  //当两棵树中只有一棵树的节点为空时，节点数量不相同时，直接返回false
        return false;
    //检查节点和值是否相同
    if(p->val != q->val)  
        return false;
    //检查左右子树是否相同
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
1
2
3
4
5
6
7
8
9
10
11
12

---

三、对称二叉树

题目链接

101. 对称二叉树 - 力扣（LeetCode）

题目描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

思路分析

这道题是上面那道题的一个简单变形，二者在实现思路上大致一样，只是细节上有所不同而已。

由于对称结构是最左边和最右边的节点相同，所以我们需要对 检查两棵子树是否对称 的代码中递归的参数进行调整：

return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
1

代码实现

//检查两棵子树是否对称
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)  //当两棵树中只有一棵树的节点为空时，节点数量不相同时，直接返回false
        return false;
    //检查节点和值是否相同
    if(p->val != q->val)  
        return false;
    //检查左右子树是否对称
    return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}

//思路：将二叉树分为左子树和右子树，检查两棵子树是否对称
bool isSymmetric(struct TreeNode* root){
    return isSameTree(root->left, root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

---

四、二叉树的前序遍历

题目链接

144. 二叉树的前序遍历 - 力扣（LeetCode）

题目描述

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

思路分析

二叉树的前序遍历在前面我们已经学过，只是这里有两点需要注意的地方：

1、由于二叉树的节点数数未知的，为了不浪费空间，我们可以先求出二叉树的节点数，然后再开辟对应大小的空间；

2、由于数据是存储在一个数组中，所以我们需要一个变量 i 来控制数组的下标；同时，由于在递归调用过程中对形参的改变不会影响实参，所以这里我们需要传递 i 的地址，通过指针来控制 i 的增长。

代码实现

// 二叉树节点个数
int BinaryTreeSize(struct TreeNode* root)
{
	if (root == NULL)
		return 0;
	//左子树节点个数+右子树节点个数+根节点
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树前序遍历
void BinaryTreePrevOrder(struct TreeNode* root, int* ret, int* pi)
{
	if (root == NULL)
	{
		return;
	}
	//先访问根，再访问左子树，最后访问右子树
	ret[*pi] = root->val;
    (*pi)++;
	BinaryTreePrevOrder(root->left, ret, pi);
	BinaryTreePrevOrder(root->right, ret, pi);
}

 //思路：求出二叉树的节点个数，然后malloc等长的数组来存储节点值，最后通过前序遍历将节点值放入数组中
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    //求二叉树节点个数
    int n = BinaryTreeSize(root);
    int* ret = (int*)malloc(sizeof(struct TreeNode)*n);
    //前序遍历
    int i = 0;
    BinaryTreePrevOrder(root, ret, &i);
    *returnSize = i;
    return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

---

五、二叉树的中序遍历

题目链接

94. 二叉树的中序遍历 - 力扣（LeetCode）

题目描述

给定一个二叉树的根节点 root ，返回它的 中序 遍历* 。

思路分析

前序遍历和中序遍历基本上是一样的，只是访问顺序改变而已。

代码实现

// 二叉树节点个数
int BinaryTreeSize(struct TreeNode* root)
{
	if (root == NULL)
		return 0;
	//左子树节点个数+右子树节点个数+根节点
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树中序遍历
void BinaryTreeInOrder(struct TreeNode* root, int* ret, int* pi)
{
	if (root == NULL)
	{
		return;
	}
	//先访问左子树，再访问根，最后访问右子树
	BinaryTreeInOrder(root->left, ret, pi);
	ret[*pi] = root->val;
    (*pi)++;
	BinaryTreeInOrder(root->right, ret, pi);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
    //求二叉树节点个数
    int n = BinaryTreeSize(root);
    int* ret = (int*)malloc(sizeof(struct TreeNode)*n);
    //前序遍历
    int i = 0;
    BinaryTreeInOrder(root, ret, &i);
    *returnSize = i;
    return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

---

六、二叉树的后序遍历

题目链接

145. 二叉树的后序遍历 - 力扣（LeetCode）

题目描述

给定一个二叉树的根节点 root ，返回它的 后序 遍历 。

思路分析

后序遍历和前序、中序遍历基本上是一样的，只是访问顺序改变而已。

代码实现

// 二叉树节点个数
int BinaryTreeSize(struct TreeNode* root)
{
	if (root == NULL)
		return 0;
	//左子树节点个数+右子树节点个数+根节点
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树前序遍历
void BinaryTreePostOrder(struct TreeNode* root, int* ret, int* pi)
{
	if (root == NULL)
	{
		return;
	}
	//先访问根，再访问左子树，最后访问右子树
	BinaryTreePostOrder(root->left, ret, pi);
	BinaryTreePostOrder(root->right, ret, pi);
    ret[*pi] = root->val;
    (*pi)++;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize){
    //求二叉树节点个数
    int n = BinaryTreeSize(root);
    int* ret = (int*)malloc(sizeof(struct TreeNode)*n);
    //前序遍历
    int i = 0;
    BinaryTreePostOrder(root, ret, &i);
    *returnSize = i;
    return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

---

七、另一棵树的子树

题目链接

572. 另一棵树的子树 - 力扣（LeetCode）

题目描述

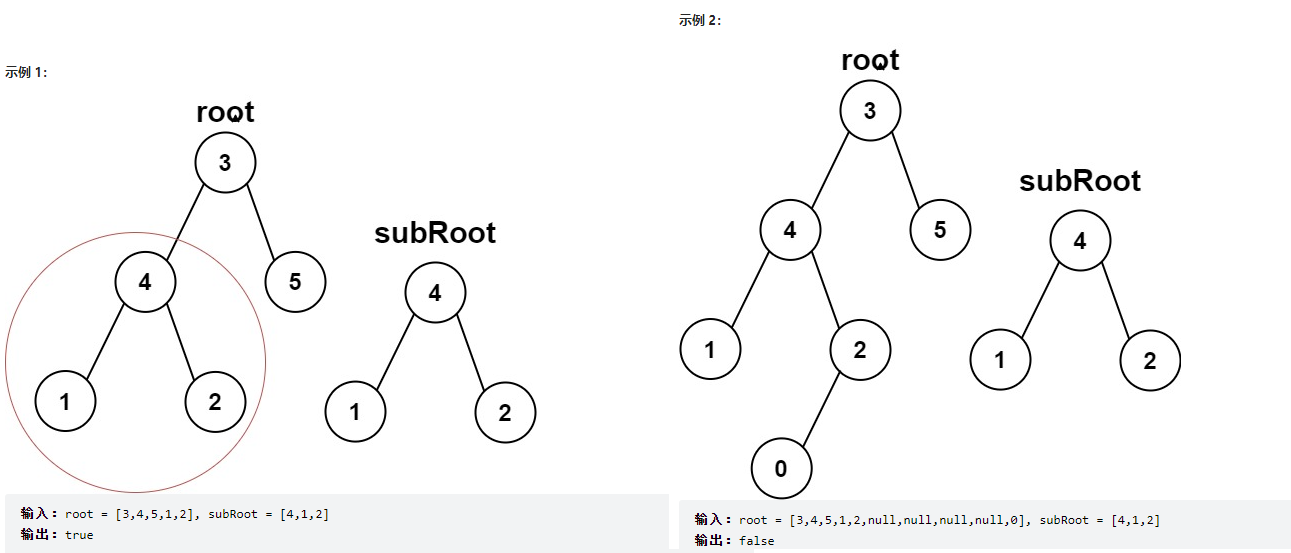
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

思路分析

由于root 和 subRoot 中可能含有一个或多个值相同的节点，所以我们只能遍历root，取出其中的每一个节点与subRoot进行比较，看是否相同。

代码实现

//思路：检查节点的值或者节点的数量是否相同，如果不同直接返回false，然后递归检查左右子树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)  //当两棵树中只有一棵树的节点为空时，节点数量不相同时，直接返回false
        return false;
    //检查节点和值是否相同
    if(p->val != q->val)  
        return false;
    //检查左右子树是否相同
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

//思路：遍历root，取root的每一棵子树与sunroot比较，如果相同，就返回true
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root == NULL)
        return false;
    if(isSameTree(root, subRoot))
        return true;
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

---

九、二叉树构建及遍历

题目链接

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

题目描述

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

示例1

输入：abc##de#g##f###
输出：c b e g d f a 
1
2

思路分析

这道题就是把二叉树的构建和二叉树的遍历结合到了一起而已，我们分别完全这两个功能即可。

代码实现

#include 
#include 

//符号和结构的定义
typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	if (a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}

	//创建根节点
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	root->data = a[*pi];
	(*pi)++;

	//创建左右子树
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);

	return root;
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//先访问左子树，再访问根，最后访问右子树
	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);
	BinaryTreeInOrder(root->right);
}

int main()
{
    char arr[100];
    scanf("%s", arr);
    
    //构建二叉树
    int i = 0;
    BTNode* root = BinaryTreeCreate(arr, &i);
    
    //二叉树的中序遍历
    BinaryTreeInOrder(root);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

---