拉普拉斯特征映射（Laplacian Eigenmaps, LE）

主要思想

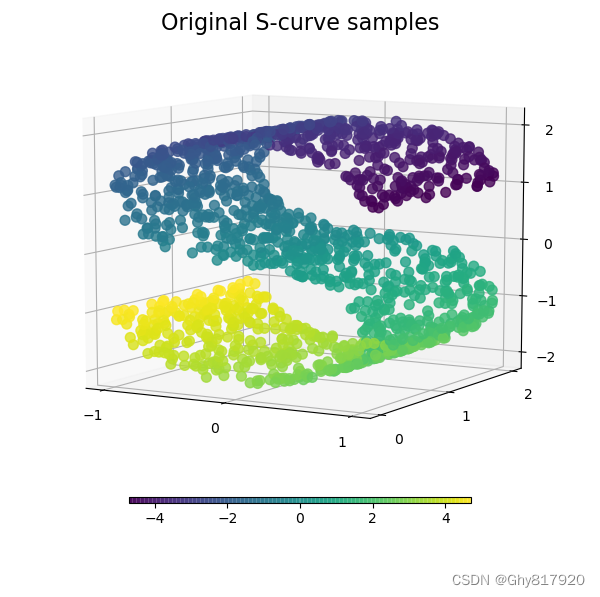
LE将$D$维特征$\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N]\in {\mathbb{R}}^{D\times N}$（${\mathbf{x}}_i\in {\mathbb{R}}^D$）映射到$d(d\ll D)$维空间中（$\mathbf{Y}=[{\mathbf{y}}_1,{\mathbf{y}}_2,\cdots ,{\mathbf{y}}_N]\in {\mathbb{R}}^{d\times N}$），使得在降维后的空间中，尽量使在原始空间$\mathbf{X}$中近的点在新的空间$\mathbf{Y}$中仍然近，远的仍然远。

推导方法

根据原始数据$\mathbf{X}$构造无向加权图邻接矩阵$\mathbf{W}\in {\mathbb{R}}^{N\times N}$（距离越近的两个点，权重越大），根据此矩阵构造度数矩阵
D = [ ∑ i W 1 , i ∑ i W 2 , i ⋱ ∑ i W N , i ] \mathbf{D}=\left[ ∑iW1,i∑iW2,i⋱∑iWN,i

\right] D=⎣ ⎡​∑i​W1,i​​∑i​W2,i​​⋱​∑i​WN,i​​⎦ ⎤​
那么拉普拉斯矩阵$\mathbf{L}=\mathbf{D}-\mathbf{W}$，所以优化目标为
$$\begin{gathered} \underset{\mathbf{Y}}{\mathrm{argmin}}\frac{1}{2}\sum _{i,j=1}^N{\mathbf{W}}_{i,j}\parallel {\mathbf{y}}_i-{\mathbf{y}}_j{\parallel }^2 \\ \underset{\mathbf{Y}}{\mathrm{argmin}}\frac{1}{2}\sum _{i,j=1}^N{\mathbf{W}}_{i,j}{\left({\mathbf{y}}_i-{\mathbf{y}}_j\right)}^T\left({\mathbf{y}}_i-{\mathbf{y}}_j\right) \\ \underset{\mathbf{Y}}{\mathrm{argmin}}\frac{1}{2}\sum _{i,j=1}^N{\mathbf{W}}_{i,j}\left({\mathbf{y}}_i^T{\mathbf{y}}_i-{\mathbf{y}}_i^T{\mathbf{y}}_j-{\mathbf{y}}_j^T{\mathbf{y}}_i+{\mathbf{y}}_j^T{\mathbf{y}}_j\right) \\ \underset{\mathbf{Y}}{\mathrm{argmin}}\sum _{i=1}^N{\mathbf{y}}_i^T{\mathbf{y}}_i\sum _{j=1}^N{\mathbf{W}}_{i,j}-\sum _{i,j=1}^N{\mathbf{W}}_{i,j}{\mathbf{y}}_i^T{\mathbf{y}}_j \\ \underset{\mathbf{Y}}{\mathrm{argmin}}trace\left(\mathbf{Y}\mathbf{D}{\mathbf{Y}}^T\right)-trace\left({\mathbf{YWY}}^T\right)\left[trace\left({\mathbf{y}}_i^T{\mathbf{y}}_j\right)=trace\left({\mathbf{y}}_j{\mathbf{y}}_i^T\right)\right] \\ \underset{\mathbf{Y}}{\mathrm{argmin}}trace\left(\mathbf{Y}\left(\mathbf{D}-\mathbf{W}\right){\mathbf{Y}}^T\right) \\ \underset{\mathbf{Y}}{\mathrm{argmin}}trace\left(\mathbf{Y}\mathbf{L}{\mathbf{Y}}^T\right) \end{gathered}$$
引入约束$\mathbf{YD}{\mathbf{Y}}^T=\mathbb{I}$（确保尺度大小不变且不会退化到更低维度空间）后的优化目标为
$$\begin{gathered} \{\begin{array}{c}\underset{\mathbf{Y}}{\mathrm{argmin}}trace\left({\mathbf{YLY}}^T\right)\\ s.t.{\mathbf{YDY}}^T=\mathbb{I}\end{array} \\ \iff \{\begin{array}{c}\underset{\mathbf{Y}}{\mathrm{argmin}}trace\left({\mathbf{ZD}}^{-1/2}{\mathbf{LD}}^{-1/2}{\mathbf{Z}}^T\right)\\ s.t.{\mathbf{ZZ}}^T=\mathbb{I}\\ \mathbf{Y}={\mathbf{ZD}}^{-1/2}\end{array} \end{gathered}$$
由上可知，最优值$\mathbf{Y}$为矩阵${\mathbf{D}}^{-1}\mathbf{L}$所对应的最小$d$个特征值对应的特征向量的转置！

此外，由于拉普拉斯矩阵$\mathbf{L}$自身含有特征值为0的全1的特征向量，则相应的${\mathbf{D}}^{-1}\mathbf{L}$也有全1的特征向量，这样一来，所有的${\mathbf{y}}_i{|}_{i=1}^N$都有个维度的值为1，所以一般来说不取最小的0特征值对应的特征向量，从倒数第二小的特征值对应的特征向量开始取。

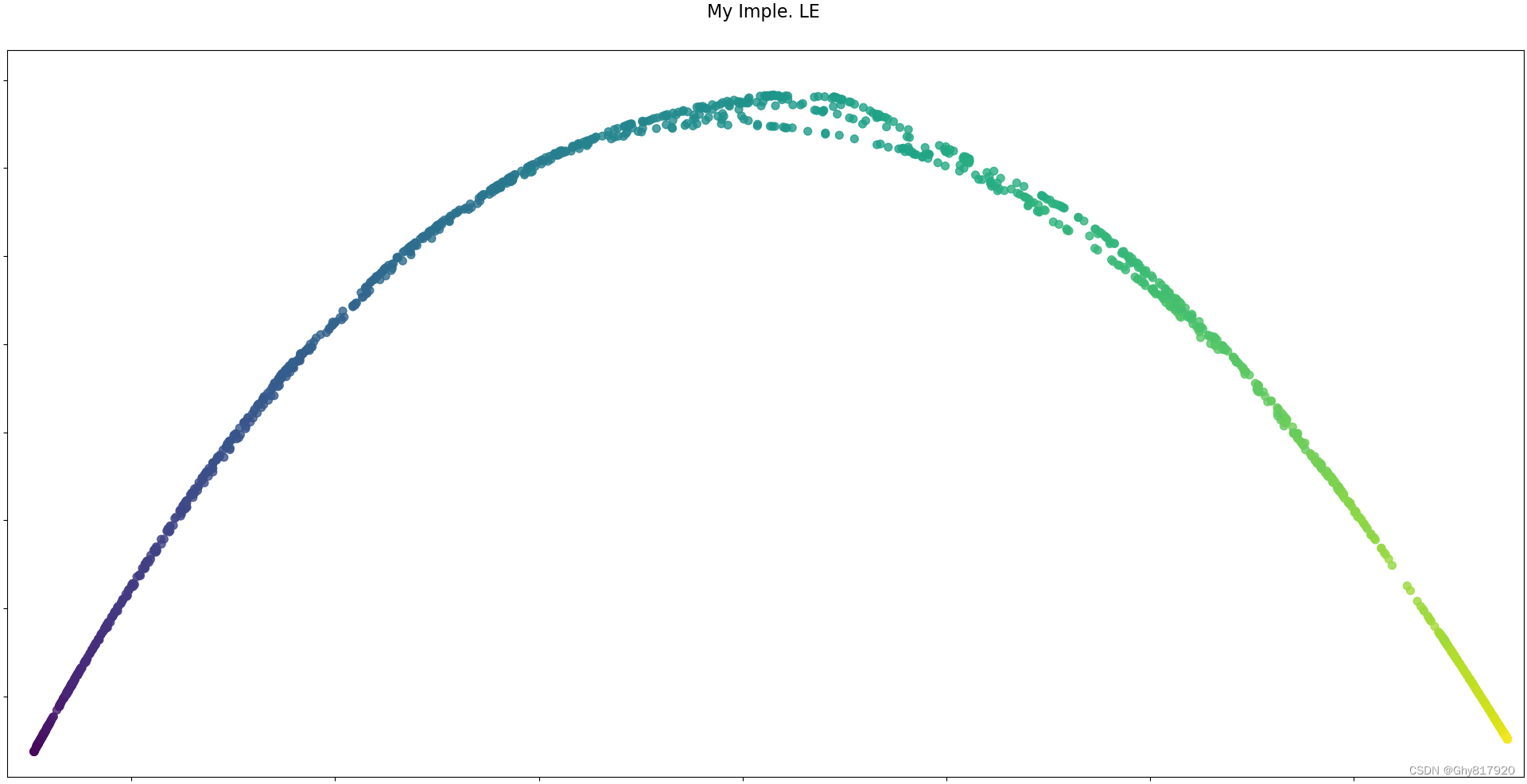
from numpy.random import RandomState
import matplotlib.pyplot as plt
from matplotlib import ticker

# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d  # noqa: F401

from sklearn import manifold, datasets
import numpy as np
from scipy.sparse import diags

rng = RandomState(0)

n_samples = 1500
S_points, S_color = datasets.make_s_curve(n_samples, random_state=rng)

def plot_3d(points, points_color, title):
    x, y, z = points.T

    fig, ax = plt.subplots(
        figsize=(6, 6),
        facecolor="white",
        tight_layout=True,
        subplot_kw={"projection": "3d"},
    )
    fig.suptitle(title, size=16)
    col = ax.scatter(x, y, z, c=points_color, s=50, alpha=0.8)
    ax.view_init(azim=-60, elev=9)
    ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
    ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
    ax.zaxis.set_major_locator(ticker.MultipleLocator(1))

    fig.colorbar(col, ax=ax, orientation="horizontal", shrink=0.6, aspect=60, pad=0.01)
    # plt.show()


def plot_2d(points, points_color, title):
    fig, ax = plt.subplots(figsize=(3, 3), facecolor="white", constrained_layout=True)
    fig.suptitle(title, size=16)
    add_2d_scatter(ax, points, points_color)
    # plt.show()


def add_2d_scatter(ax, points, points_color, title=None):
    x, y = points.T
    ax.scatter(x, y, c=points_color, s=50, alpha=0.8)
    ax.set_title(title)
    ax.xaxis.set_major_formatter(ticker.NullFormatter())
    ax.yaxis.set_major_formatter(ticker.NullFormatter())

def sklearn_le():
    spectral = manifold.SpectralEmbedding(
    n_components=n_components, n_neighbors=n_neighbors
    )
    S_spectral = spectral.fit_transform(S_points)

    plot_2d(S_spectral, S_color, "Sklearn LE")

def my_le():
    # 借助sklearn LE 构造邻接矩阵 偷个懒！！
    spectral = manifold.SpectralEmbedding(
    n_components=n_components, n_neighbors=n_neighbors
    )
    W = spectral._get_affinity_matrix(S_points).toarray()
    D = np.diag(np.sum(W, axis=1))
    

    S = np.diag(1. / np.sum(W, axis=1)) @ (D - W)

    values, vectors = np.linalg.eig(S)
    idxs = np.argsort(values)
    
    # 除去最小的0特征向量
    W = vectors[:,[idxs[i] for i in range(1,3)]]
    W[:,0] = -W[:,0] #确保与sklearn一样

    plot_2d(W, S_color, "My Imple. LE")


if __name__ == "__main__":
    n_neighbors = 12  # neighborhood which is used to recover the locally linear structure
    n_components = 2  # number of coordinates for the manifold

    plot_3d(S_points, S_color, "Original S-curve samples")

    sklearn_le()

    my_le()

    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90