数据结构（C++）[B树（B-树）插入与中序遍历，效率分析]、B+树、B*树、B树系列应用

1. B树(B-树)

B树系列常用作查找使用（外查找）

其他常见的查找搜索结构

B树使用场景：
数据量很大，无法直接讲数据放入内存中，这些数据在磁盘上。

B树的结构中，树中的节点保存的是数据在磁盘中的位置。

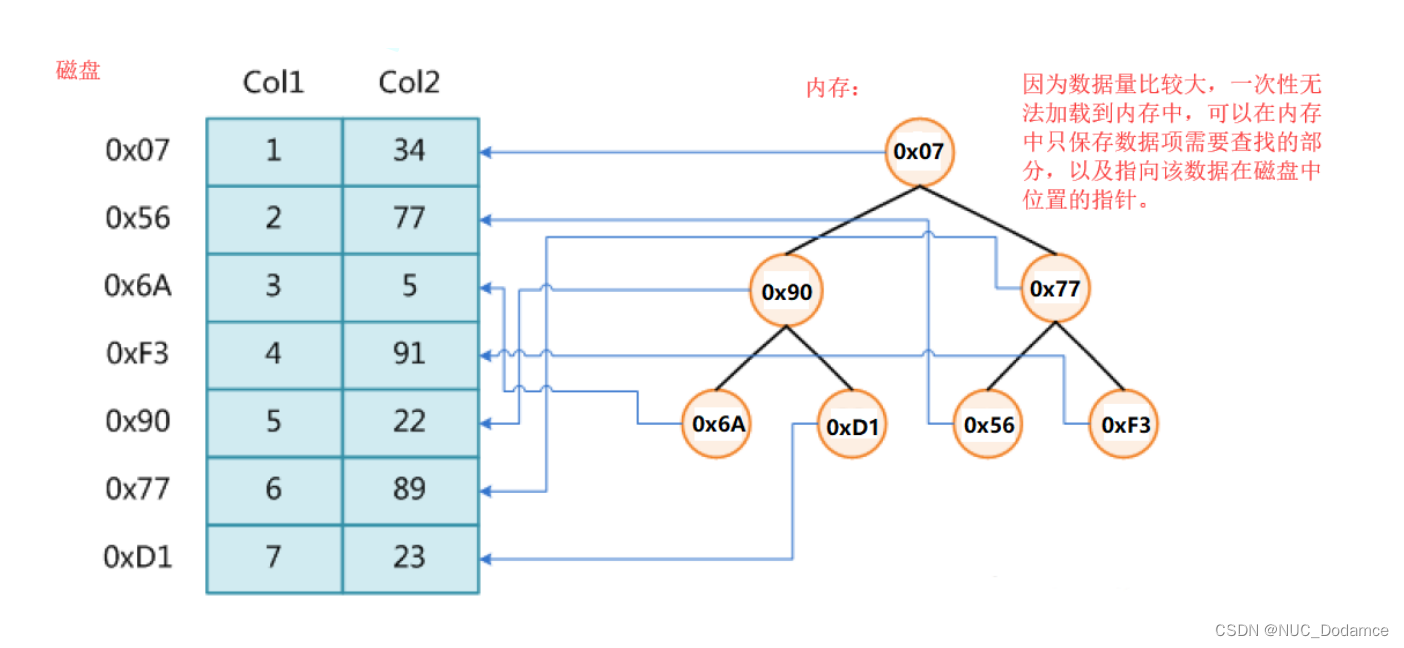
但是如果B树是类似AVL树，红黑树或哈希表的话，涉及大量的访问磁盘操作，效率太低。

B树采用的是优化AVL树的方式提高效率

1. 将普通的AVL树进行压缩（单层存更多），二叉树变成多叉树。
2. 一个节点有多个关键字和其映射的值

B树的规则

一棵m阶(m>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性质：

1. 根节点至少有两个孩子
2. 每个分支节点都包含k-1个关键字和k个孩子，其中 ceil(m/2) ≤ k ≤ m ceil是向上取整函数（分支节点，孩子比关键字多一个，eg：10阶B树，每个分支节点最少包含5个孩子，4个关键字。最多包含10个孩子，9个关键字）
3. 每个叶子节点都包含k-1个关键字，其中 ceil(m/2) ≤ k ≤ m
4. 所有的叶子节点都在同一层
5. 每个节点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6. 每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）其中，Ki(1≤i≤n)为关键字，且Ki

B树插入过程

eg：三阶B树插入关键字（53, 139, 75, 49, 145, 36, 50, 47, 101）

节点最多保存2个关键字，最少保存1个关键字。根节点单独看

1. 根节点最多可以保存2个关键字，为了简化插入操作，开辟三个关键字大小，当插入后发现已经满了时再进行分裂。同时多开辟一个空间也有助于在插入时进行排序。
   
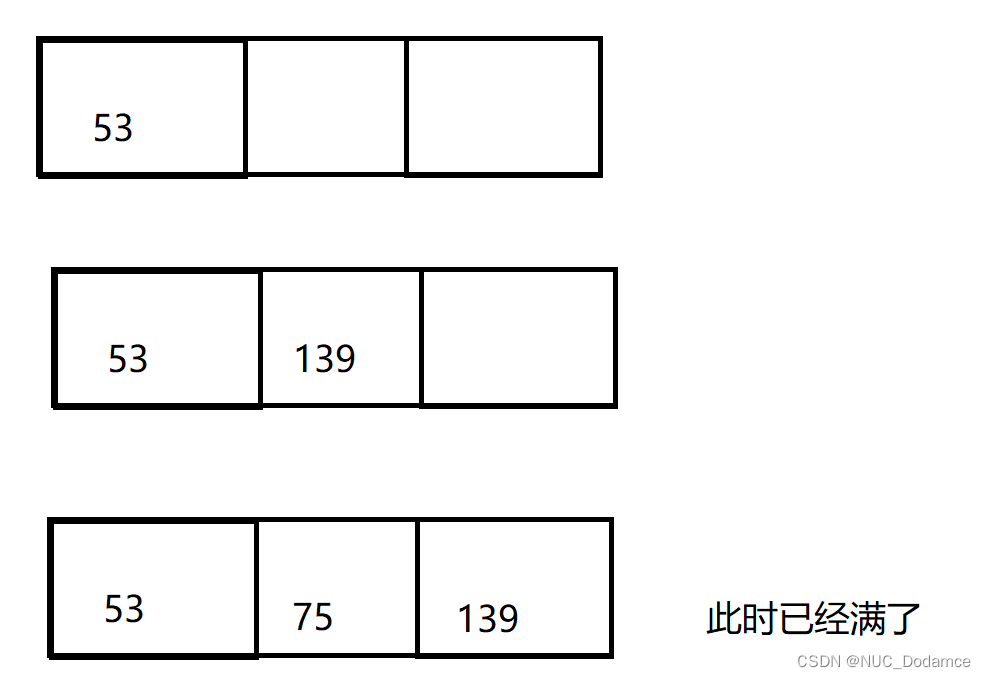
2. 如果节点满了，分裂右边一半关键字个数的一般给兄弟节点。提取中位数给父亲，没有父亲就创建新的根节点
   
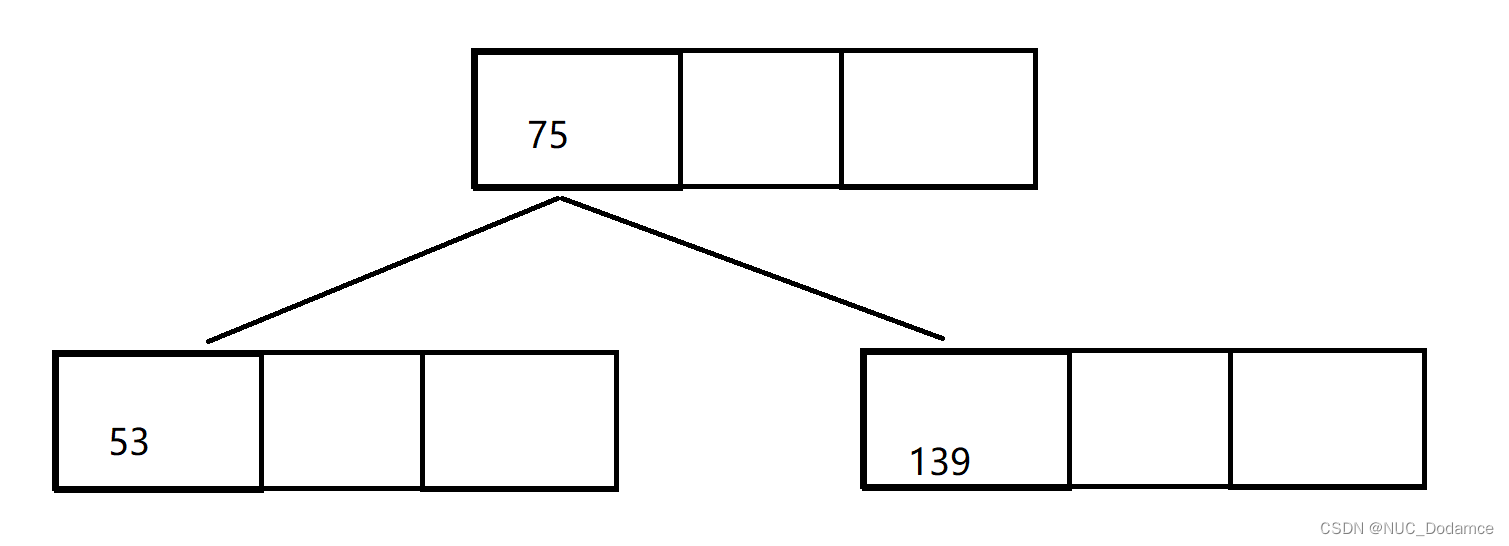
3. 继续插入49等后续关键字。
   
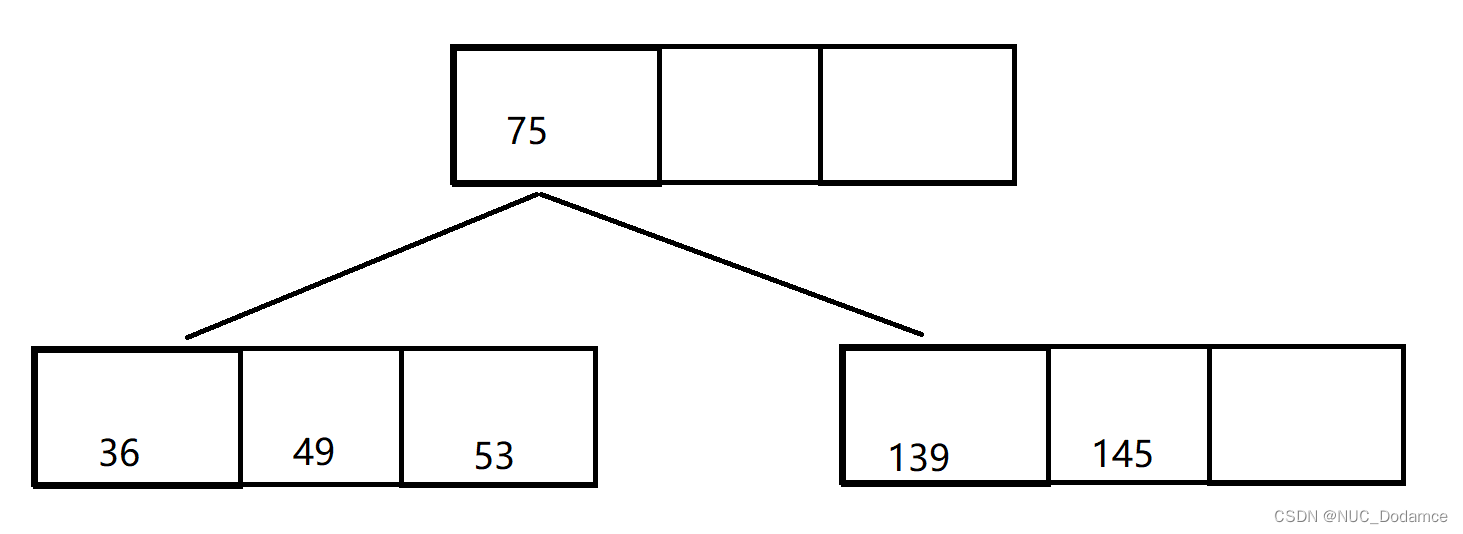
   此时节点又满了，需要进行分裂。
   
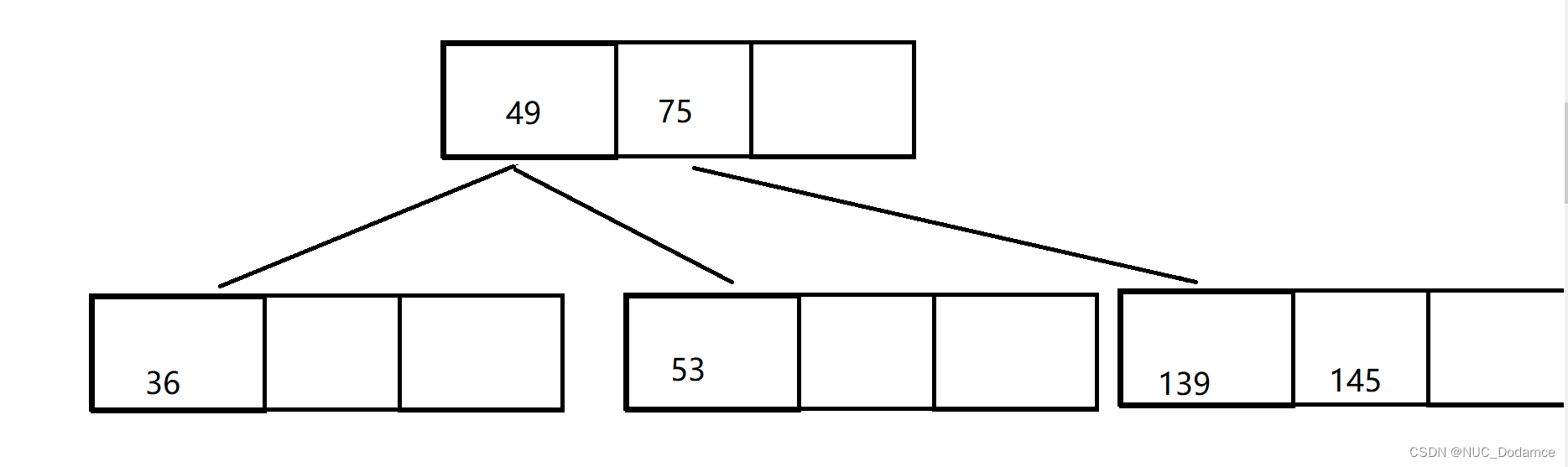
4. 继续插入50和47这两个关键字。
   
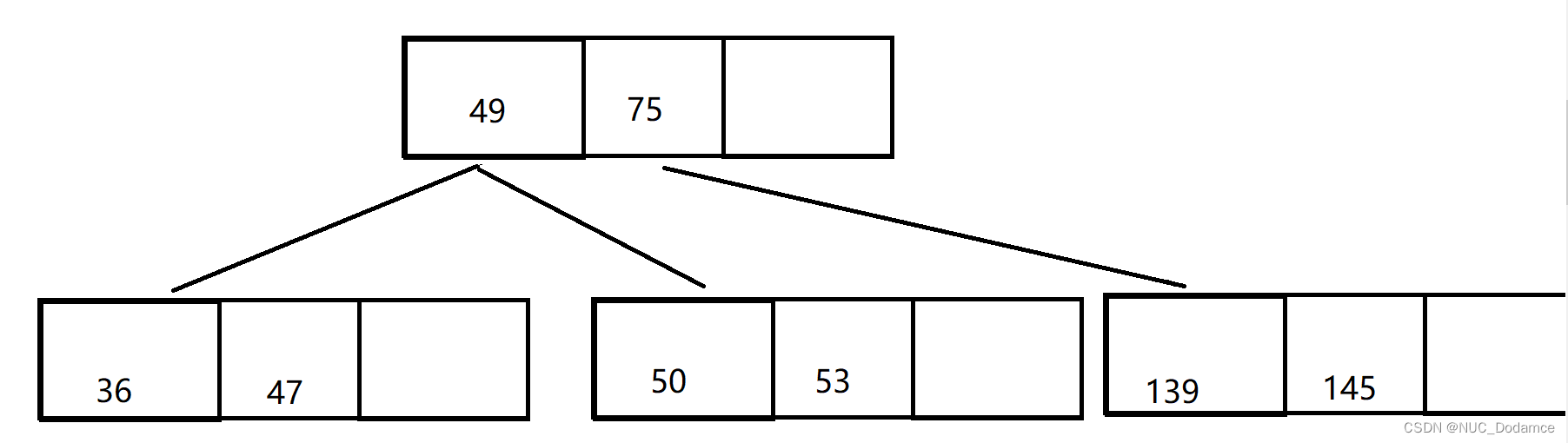
5. 最后插入101，导致叶子节点满，需要进行分裂
   

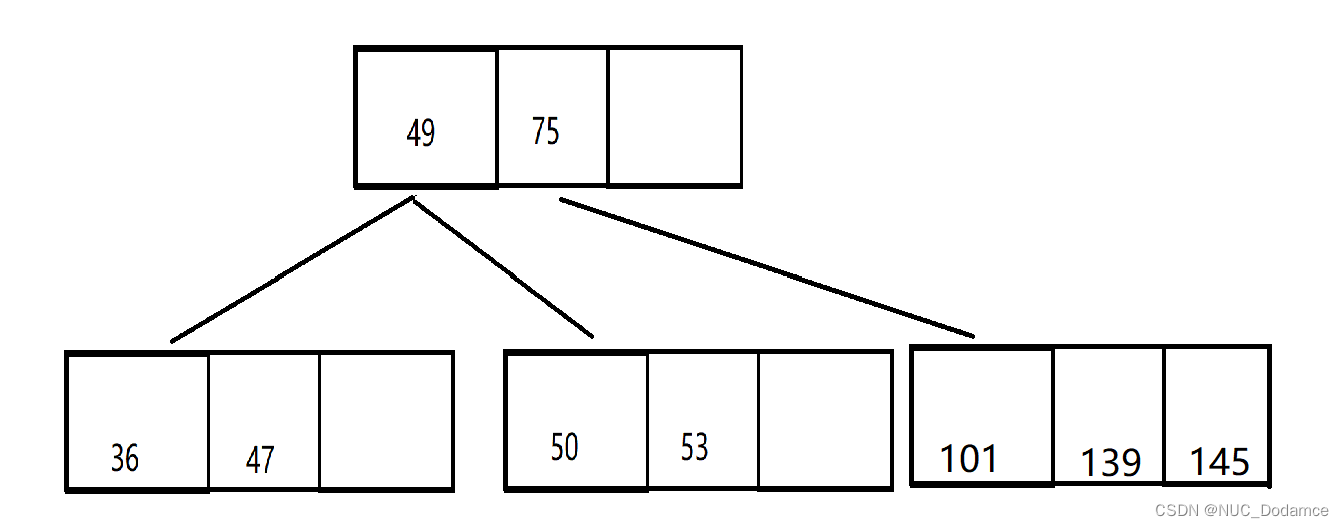
这次分裂会导致两次连续分裂
第一次分裂导致根节点满

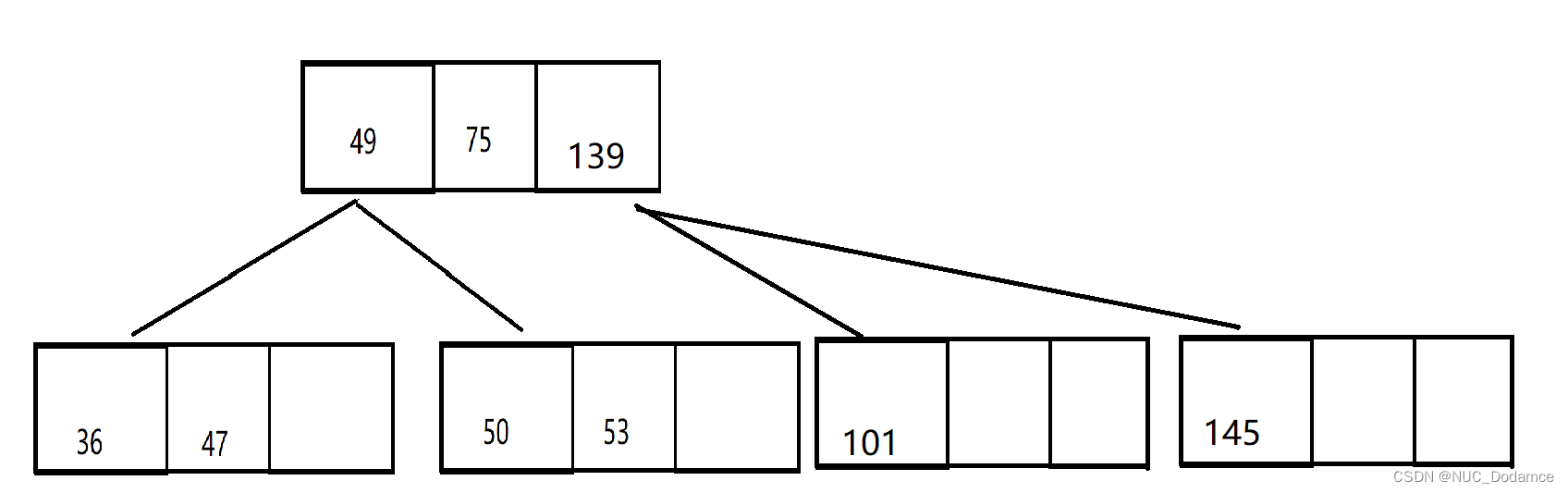
继续分裂根节点，产生新的根节点

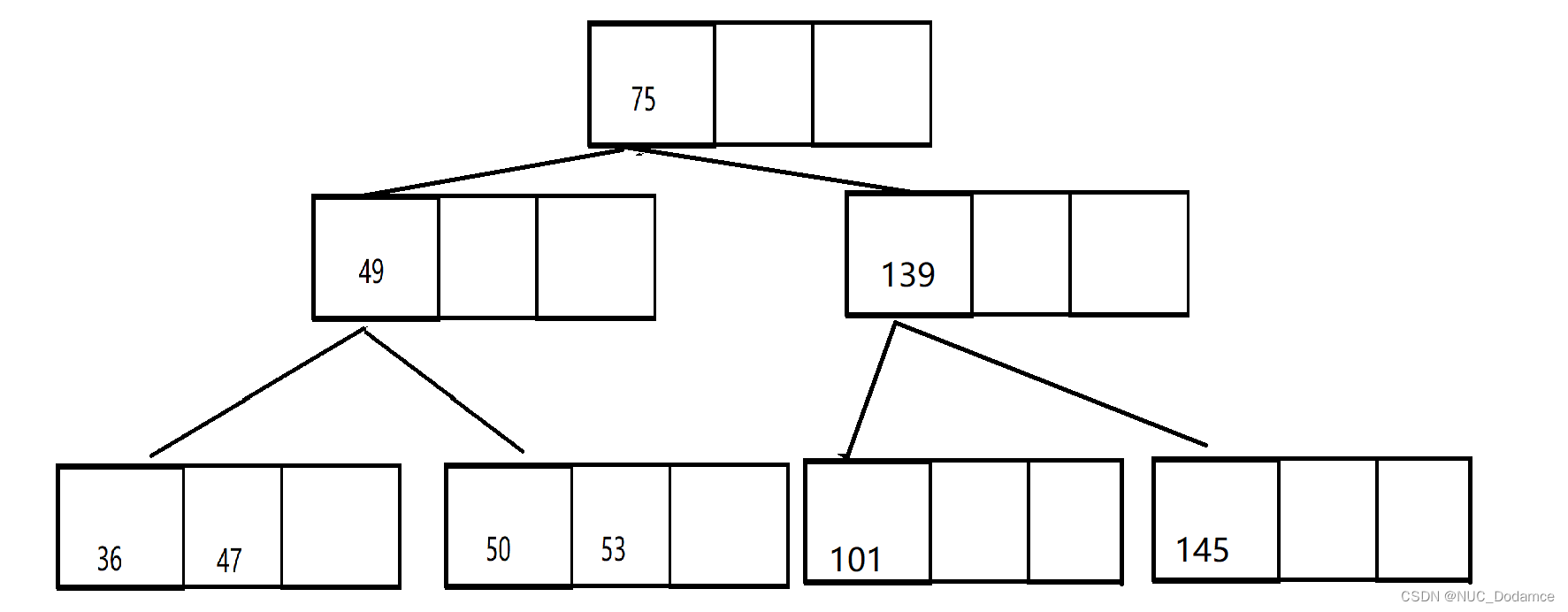
插入完毕

特点

1. B树天然平衡，B树是先横向扩展，再竖直生长。所以B树天然平衡
2. 新插入的节点一定在叶子插入，叶子节点没有孩子，不影响关键字和孩子的关系
3. 叶子节点满了，分裂出一个兄弟，提取中位数，向父亲插入一个值和孩子
4. 根节点分裂会增加一层
5. 对于B树的每一个节点，这个节点的孩子个数比关键字个数多一个。

C++模拟实现B树插入与中序遍历

#pragma once
#include

template<class K, size_t M>
struct BTreeNode {
	//多开辟一个空间方便插入
	K _keys[M];
	BTreeNode<K, M>* _subs[M + 1];
	BTreeNode<K, M>* _parent;//这个节点的父节点
	size_t _n;//记录实际存储关键字个数
	BTreeNode() {
		for (size_t i = 0; i < M; i++) {
			_keys[i] = K();
			_subs[i] = nullptr;
		}
		_subs[M] = nullptr;
		_n = 0;
		_parent = nullptr;
	}
};

//数据如果存在磁盘上，K是磁盘地址
template<class K, size_t M>
class BTree {
	typedef BTreeNode<K, M> Node;
public:
	//查找要插入的叶子节点对应的下标
	std::pair<Node*, int>Find(const K& key) {
		Node* par = nullptr;
		Node* cur = _root;
		while (cur) {
			//在一个节点中查找
			size_t i = 0;
			while (i < cur->_n) {
				if (key < cur->_keys[i]) {
					//_key[size]的左孩子
					break;
				}
				else if (key > cur->_keys[i]) {
					i++;
				}
				else {
					return std::make_pair(cur, i);
				}
			}
			par = cur;//记录cur的父节点
			cur = cur->_subs[i];
		}
		return std::make_pair(par, -1);
	}
	bool Insert(const K& key) {
		if (_root == nullptr) {
			_root = new Node;
			_root->_keys[0] = key;
			_root->_n++;
			return true;
		}
		std::pair<Node*,int> ret = Find(key);
		if (ret.second >= 0) {
			//不允许冗余
			return false;
		}
		//如果没有找到，Find函数返回要插入的叶子节点
		Node* cur = ret.first;
		K newKey = key;
		Node* child = nullptr;
		while (true) {
			InsertKey(cur, newKey, child);
			if (cur->_n == M) {
				//这个节点满了，需要分裂
				size_t mid = M / 2;
				//node中有[mid+1,M-1]的数据
				Node* node = new Node;
				size_t pos = 0;
				//同时还要拷贝孩子节点
				for (int i = mid + 1; i < M; i++) {
					node->_keys[pos] = cur->_keys[i];
					node->_subs[pos] = cur->_subs[i];
					if (cur->_subs[i] != nullptr) {
						//更新父节点
						cur->_subs[i]->_parent = node;
					}
					pos++;
					cur->_keys[i] = K();//方便观察
					cur->_subs[i] = nullptr;
				}
				//最后一个子节点拷贝
				node->_subs[pos] = cur->_subs[M];
				if (cur->_subs[M] != nullptr) {
					//更新父节点
					cur->_subs[M]->_parent = node;
				}
				cur->_subs[M] = nullptr;
				node->_n = pos;
				cur->_n -= pos + 1;//还要提取一个节点作为这两个节点的父节点

				K midKey = cur->_keys[mid];
				cur->_keys[mid] = K();//方便调试观察

				//向cur->parent插入cur->_keys[mid]和node节点
				if (cur->_parent == nullptr) {
					//分裂根节点
					_root = new Node;
					_root->_keys[0] = midKey;
					_root->_subs[0] = cur;
					_root->_subs[1] = node;
					_root->_n = 1;
					cur->_parent = _root;
					node->_parent = _root;
					break;
				}
				newKey = midKey;
				child = node; 
				cur = cur->_parent;//while循环插入
			}
			else {
				//节点没有满，插入结束
				return true;
			}
		}
		return true;
	}

	//中序遍历
	void Inorder() {
		_Inorder(_root);
	}
private:
	void _Inorder(Node* root) {
		if (root == nullptr) {
			return;
		}
		for (size_t i = 0; i < root->_n; i++) {
			_Inorder(root->_subs[i]);
			std::cout << root->_keys[i] << " ";
		}
		//最后还剩余一个右子树
		_Inorder(root->_subs[root->_n]);
	}

	void InsertKey(Node* cur, const K& key, Node* child) {
		int endPos = cur->_n - 1;
		while (endPos >= 0) {
			if (key < cur->_keys[endPos]) {
				//挪动key和右孩子
				cur->_keys[endPos + 1] = cur->_keys[endPos];
				cur->_subs[endPos + 2] = cur->_subs[endPos + 1];
				endPos -= 1;
			}
			else {
				break;
			}
		}
		cur->_keys[endPos + 1] = key;
		cur->_subs[endPos + 2] = child;
		if (child != nullptr) {
			child->_parent = cur;
		}
		cur->_n += 1;
	}
	Node* _root = nullptr;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162

测试代码：

#include"BTree.h"

int main() {
	int arr[] = { 53, 139, 75, 49, 145, 36, 50, 47, 101 };
	BTree<int, 3>bTree;
	for (auto& e : arr) {
		bTree.Insert(e);
	}
	bTree.Inorder();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11

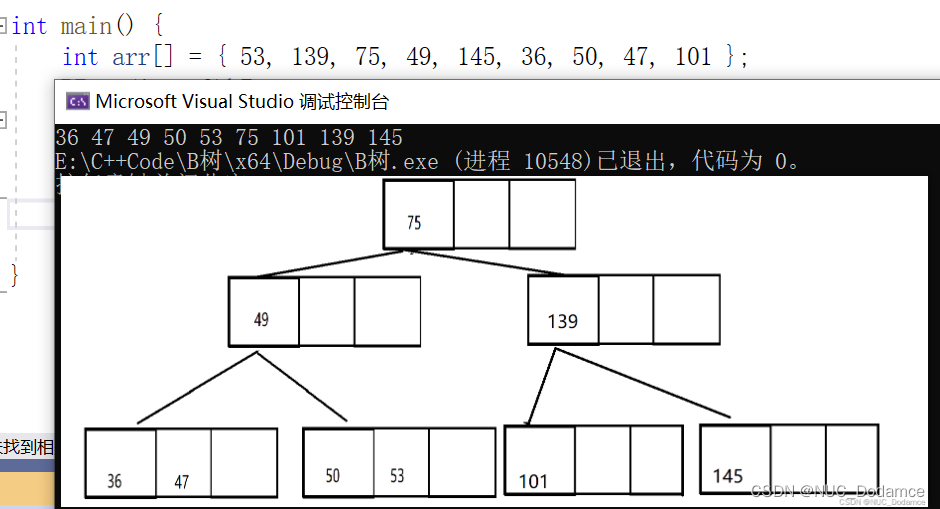
B树效率分析

时间复杂度：

设B树高度为h
第一层B树保存关键字个数大致为m个
第二层B树保存关键字个数大致为m^2
设B树总关键字个数为N
N=m + m ^ 2 + m ^ 3 +……+m ^ h

计算得到
-m+m^(h+1)=N*m-N

最终得到
h+1=logm[(N*m)-N+m]

其中N远大于m所以最终B树的时间复杂度为
O(logm(N))

2. B+树

B+树是B树的变形，是在B树的基础上优化的多路平衡搜索树，B+树的规则与B树基本类似。

B+树优化的规则如下

1. 分支节点的子树指针与关键字个数相同
2. 分支节点的子树指针p[i]指向关键字大小在[ k[i],k[i+1] ]区间之间（相比于B树取消了最左边的子树）
3. 所有叶节点增加一个链接指针链接在一起
4. 所有关键字及其映射数据都在叶子节点出现。

分支节点和叶子节点又重复的值，分支节点保存叶子节点的索引

父节点保存子节点最小值作为索引

对于Key-Value形，子节点保存key值，叶子节点保存value值

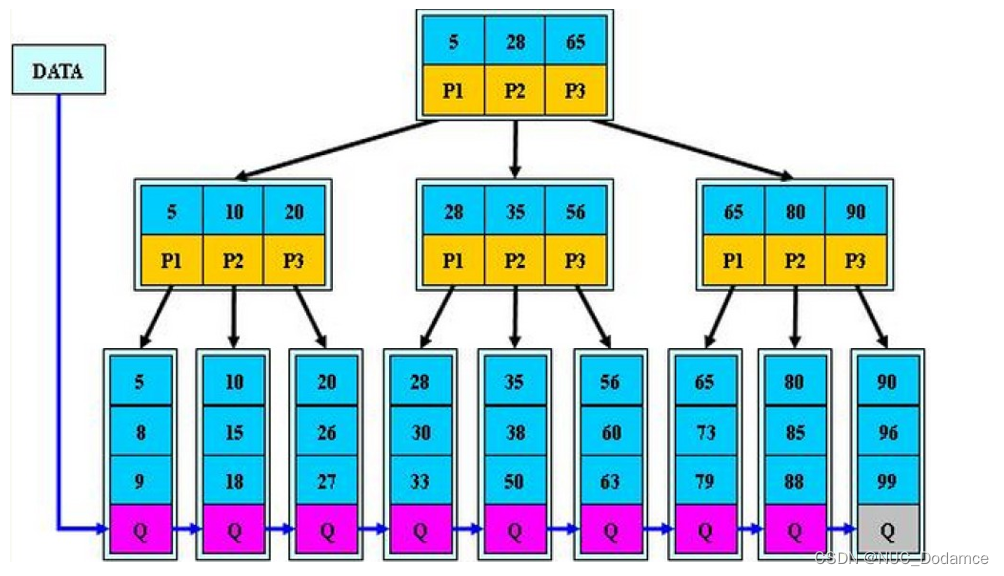
B+树插入过程

三阶B树插入关键字（53, 139, 75, 49, 145, 36, 101）

1. 开始时建立最基本的B+树结构，m=3每个节点可以保存3个关键字

插入53，139，75的过程

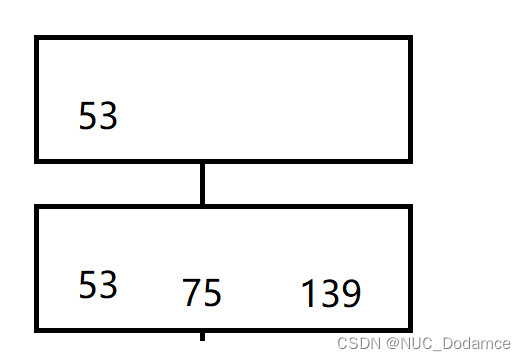
2. 之后插入49，需要进行分裂
   

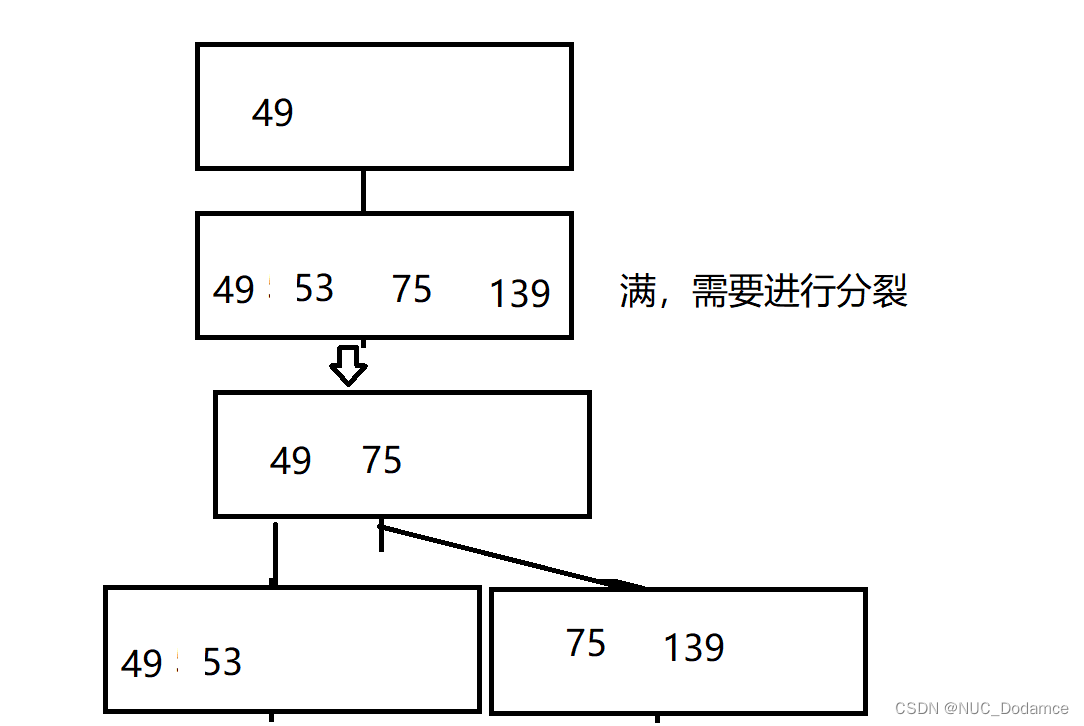
3. B*树

B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针

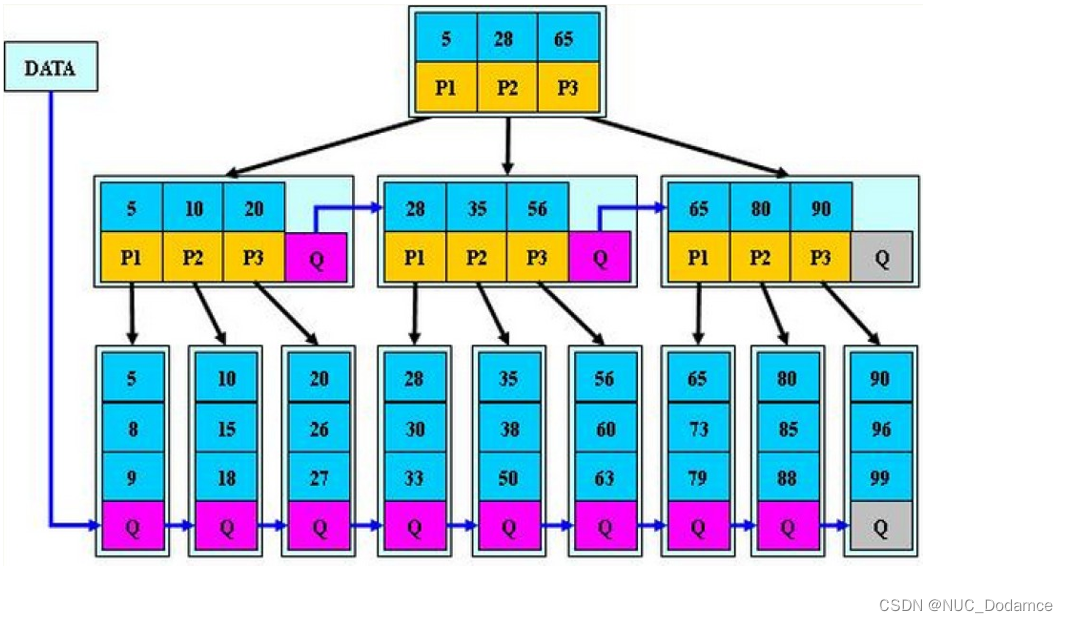
B*树想提高空间利用率

B*树分裂规则

1. 当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）
2. 如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

所以，分裂后原节点，兄弟节点，新节点各个都有2/3的数据，B*树分配新结点的概率比B+树要低，且新节点与原来节点的数据均分，空间使用率更高

4. B树应用

B树系列可以在内存中做内查找。但是相比于哈希和平衡搜索树

1. 从空间利用率来讲消耗高。
2. 插入删除数据，分裂合并节点，需要挪动数据
3. B树的高度低，但是在内存中来讲，跟哈希和平衡搜索树是一个量级。

B树系列通常在内存中体现不出优势

B树系列通常在磁盘中可以体现出优势

B树系列通常的应用作为索引使用，MySQL数据库索引底层原理是B+树

B+树索引磁盘数据