leetcode 50. Pow(x, n) (快速幂)

​
​

作者简介：C/C++ 、Golang 领域耕耘者，创作者
个人主页：作者主页
活动地址：CSDN21天学习挑战赛
题目来源： leetcode官网
如果感觉博主的文章还不错的话，还请关注➕ 、点赞👍 、收藏🧡三连支持一下博主哦~~~

💜 题目描述

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xⁿ ）。

示例1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-2³¹ <= n <= 2³¹-1
-10⁴ <= xⁿ <= 10⁴

🧡 算法分析

此题方法是用快速幂

分析：

1. 如果此题按照定义直接将n 个x 相乘，时间复杂度为O(n), 会超时。
2. 这题思路是将n 分解成二进制的数，然后预处理x的二进制次方，若n的二进制的第k位是1，则答案可以乘上x 的2^k次方。
3. 计算x 的2^k次方，自需每次将自身做平方即可。

注意：需要用long类型的num专门存n的绝对值，因为int范围是[-2147483648,2147483647]，若n取到-2147483648取绝对值后变成2147483648会爆int范围

核心：
快速幂的核心思想：

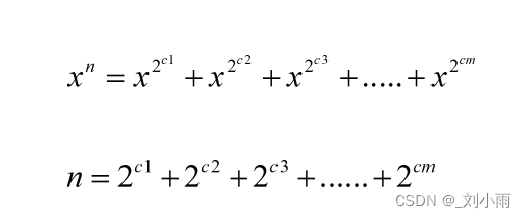
就是需要把n 拆分成二进制表示，然后就可以根据n 的二进制表示来加速计算

如果n 的第k为1，则需要乘上x 的2^k次方，计算x 的2^k次方，自需每次将自身做平方即可。

递归预处理二进制幂：

示例：

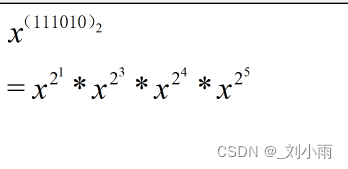
💚 代码实现

class Solution {
public:
    double myPow(double x, int n) {
        typedef long long LL;  // 因为n 可能为负无穷，取绝对值会越界，这里用long long 转化一下
        bool is_minus = n < 0;
        double re = 1;
        // 可以边预处理，边计算
        for(LL k = abs(LL(n)); k ; k >>= 1)
        {
            if(k & 1) re *= x;  // 计算
            x *= x;  // 预处理
        }

        if(is_minus) re = 1 / re;

        return re;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

执行结果：

💙 时间复杂度分析

只进行O(logn)次乘法运算，故时间复杂度为O(logn)

如果觉得对你有帮助的话:
👍 点赞，你的认可是我创作的动力！
🧡 收藏，你的青睐是我努力的方向！
✏️ 评论，你的意见是我进步的财富！