1013 Battle Over Cities

0、题目

It is vitally important to have all the cities connected by highways in a war. If a city is occupied by the enemy, all the highways from/toward that city are closed. We must know immediately if we need to repair any other highways to keep the rest of the cities connected. Given the map of cities which have all the remaining highways marked, you are supposed to tell the number of highways need to be repaired, quickly.

For example, if we have 3 cities and 2 highways connecting city1-city2 and city1-city3. Then if city1 is occupied by the enemy, we must have 1 highway repaired, that is the highway city2-city3.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 3 numbers N (<1000), M and K, which are the total number of cities, the number of remaining highways, and the number of cities to be checked, respectively. Then M lines follow, each describes a highway by 2 integers, which are the numbers of the cities the highway connects. The cities are numbered from 1 to N. Finally there is a line containing K numbers, which represent the cities we concern.

Output Specification:

For each of the K cities, output in a line the number of highways need to be repaired if that city is lost.

Sample Input:

3 2 3
1 2
1 3
1 2 3
1
2
3
4

Sample Output:

1
0
0
1
2
3

1、大致题意

给定一张城市地图，要求求出其中的一个城市被占领后要修的最少的道路，使剩余城市之间仍然连通。

2、基本思路

图论的题目，可以等价于 $求连通子集的个数-1$ ，那么就很自然地想到了并查集，毕竟一个集合中的就是一个连通子集。

设置一个邻接表，对于每个占领城市的输入，绕开它把其他存在边的结点合并，再数集合元素的个数，最后减一。

3、解题过程

3.1 并查集知识点

首先是复习并查集的相关知识点。

3.1.1 初始化

void init(){
	for(int i=1;i<=n;i++){
        fa[i]=i;//把结点i的集合号初始化为其自身编号
	}
}
1
2
3
4
5

3.1.2 查找

3.1.2.1 版本一

int find(int i){
	while(i!=fa[i]){
        i=fa[i]=fa[fa[i]];
    }
	return fa[i];
}
1
2
3
4
5
6

3.1.2.2 版本二

int find(int x) {
    if(x != fa[x]){//当x不等于它的爸爸时(当它是祖先时，它没有爸爸) 
         fa[x] = find(fa[x]);//继续找他的爸爸的爸爸 
    }
    return fa[x];//返回祖先 
}//查找 
1
2
3
4
5
6

3.1.3 合并

void unity(int x, int y){
    int r1 = find(x);//找到x的祖先 
    int r2 = find(y);//找到y的祖先 
    if(r1!=r2){
        fa[r1] = r2;//祖先和祖先结为父子(谁是父亲谁是儿子都可以) 
    }
}//合并 
1
2
3
4
5
6
7

3.2 第一次提交（7/25）

将邻接表和并查集相结合，就得到了第一稿的代码

#include
#include
#include
#include
using namespace std;
int n,m,k;
int fa[101000];
int head[101000],vis[101000],dis[101000],cnt;

struct Edge {
	int v,w,next;
} edge[501000],tmp;

void addEdge(int u, int v,int w) {
	edge[++cnt].v=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt;
}

void init() { //并查集初始化
	for(int i=1; i<=n; i++) {
		fa[i]=i;
	}
}

int find(int x) { //并查集查找
	if(x != fa[x]) { //当x不等于它的爸爸时(当它是祖先时，它没有爸爸)
		fa[x] = find(fa[x]);//继续找他的爸爸的爸爸
	}
	return fa[x];//返回祖先
}//查找


void unity(int x, int y) { //并查集合并
	int r1 = find(x);//找到x的祖先
	int r2 = find(y);//找到y的祖先
	if(r1!=r2) {
		fa[r1] = r2;//祖先和祖先结为父子(谁是父亲谁是儿子都可以)
	}
}//合并


int main() {
	cin>>n>>m>>k;

	cnt=0;
	int a,b;
	for(int i=0; i<m; i++) {
		cin>>a>>b;
		addEdge(a,b,1);
	}

	set<int> con;
	for(int i=0; i<k; i++) {
		cin>>a;
		init();
		for(int j=1; j<=n; j++) {
			if(j==a) {
				continue;
			} else {
				tmp=edge[head[j]];
				while(tmp.next!=0) {
					unity(j,tmp.v);
					tmp=edge[tmp.next];
				}
				unity(j,tmp.v);
			}
		}
		b=0;
		con.clear();
		for(int j=1; j<=n; j++) {
			b=find(j);
			con.insert(b);
		}
		cout<<con.size()-1<<endl;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

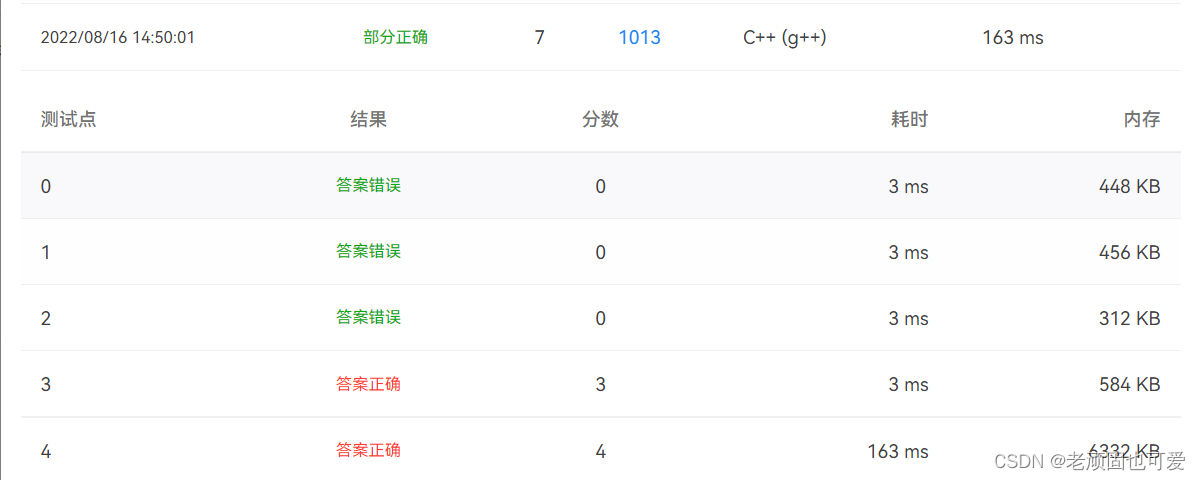
3.3 无向图问题（22/25）

首先，这题是个无向图，所以在存储的时候，需要将一条边存两次（两个顶点后面链表中都有）

for(int i=0; i<m; i++) {
	cin>>a>>b;
	addEdge(a,b,1);
	addEdge(b,a,1);
}
1
2
3
4
5

然后，变成无向图后，在并查集unity的过程中，不仅要防止 u-> 的，还要防止 ->u 的部分。

#include
#include
#include
#include
using namespace std;
int n,m,k;
int fa[101000];
int head[101000],vis[101000],dis[101000],cnt;
set<int> con;

struct Edge {
	int v,w,next;
} edge[501000],tmp;

void addEdge(int u, int v,int w) {
	edge[++cnt].v=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt;
}

void init() { //并查集初始化
	for(int i=1; i<=n; i++) {
		fa[i]=i;
	}
}

int find(int x) { //并查集查找
	if(x != fa[x]) { //当x不等于它的爸爸时(当它是祖先时，它没有爸爸)
		fa[x] = find(fa[x]);//继续找他的爸爸的爸爸
	}
	return fa[x];//返回祖先
}//查找


void unity(int x, int y) { //并查集合并
	int r1 = find(x);//找到x的祖先
	int r2 = find(y);//找到y的祖先
	if(r1!=r2) {
		fa[r1] = r2;//祖先和祖先结为父子(谁是父亲谁是儿子都可以)
	}
}//合并


int main() {
	cin>>n>>m>>k;
	
	cnt=0;
	int a,b;
	for(int i=0; i<m; i++) {
		cin>>a>>b;
		addEdge(a,b,1);
		addEdge(b,a,1);
	}

	for(int i=0; i<k; i++) {
		con.clear();
		b=0;
		cin>>a;
		init();
		for(int j=1; j<=n; j++) {
			if(j==a) {
				continue;
			} else {
				tmp=edge[head[j]];
				while(tmp.next!=0) {
					if(tmp.v!=a) {
						unity(j,tmp.v);
					}
					tmp=edge[tmp.next];
				}
				if(tmp.v!=a) {
					unity(j,tmp.v);
				}
			}
		}
		for(int j=1; j<=n; j++) {
			if(j!=a) {
				b=find(j);
				con.insert(b);
			}
		}
		cout<<con.size()-1<<endl;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

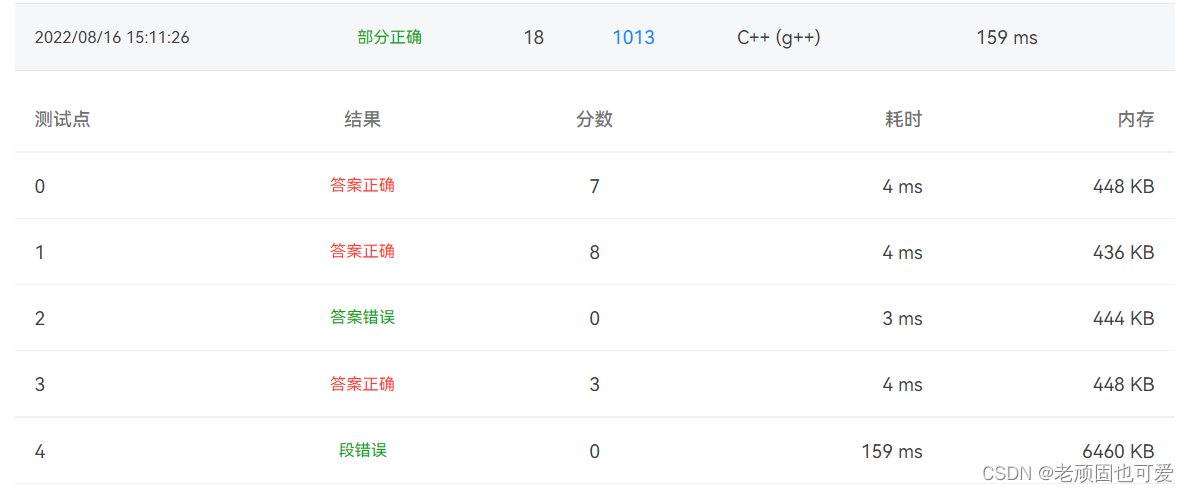
出现段错误，很显然有数组越界了，思考了一下，可能是将边存储了两遍，使得下标越界了。修改 edge[501000] 为 edge[10001000]。

#include
#include
#include
#include
using namespace std;
int n,m,k;
int fa[101000];
int head[101000],vis[101000],dis[101000],cnt;
set<int> con;

struct Edge {
	int v,w,next;
} edge[10001000],tmp;

void addEdge(int u, int v,int w) {
	edge[++cnt].v=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt;
}

void init() { //并查集初始化
	for(int i=1; i<=n; i++) {
		fa[i]=i;
	}
}

int find(int x) { //并查集查找
	if(x != fa[x]) { //当x不等于它的爸爸时(当它是祖先时，它没有爸爸)
		fa[x] = find(fa[x]);//继续找他的爸爸的爸爸
	}
	return fa[x];//返回祖先
}//查找


void unity(int x, int y) { //并查集合并
	int r1 = find(x);//找到x的祖先
	int r2 = find(y);//找到y的祖先
	if(r1!=r2) {
		fa[r1] = r2;//祖先和祖先结为父子(谁是父亲谁是儿子都可以)
	}
}//合并


int main() {
	cin>>n>>m>>k;
	cnt=0;
	int a,b;
	for(int i=0; i<m; i++) {
		cin>>a>>b;
		addEdge(a,b,1);
		addEdge(b,a,1);
	}

	for(int i=0; i<k; i++) {
		con.clear();
		b=0;
		cin>>a;
		init();
		for(int j=1; j<=n; j++) {
			if(j==a) {
				continue;
			} else {
				tmp=edge[head[j]];
				while(tmp.next!=0) {
					if(tmp.v!=a) {
						unity(j,tmp.v);
					}
					tmp=edge[tmp.next];
				}
				if(tmp.v!=a) {
					unity(j,tmp.v);
				}
			}
		}
		for(int j=1; j<=n; j++) {
			if(j!=a) {
				b=find(j);
				con.insert(b);
			}
		}
		cout<<con.size()-1<<endl;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

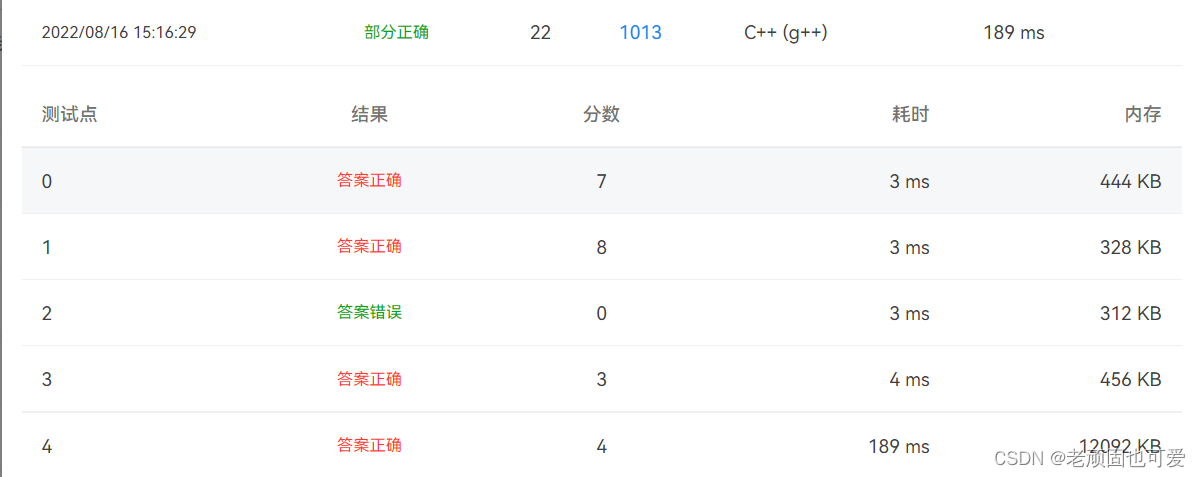
成功拿下第四个用例（22/25）

3.4 最后一城 - 邻接表中的链表判断结尾（22/25）

在一次一次的测试后，想到了一种极端情况，就是下面这种用例

输入：
3 0 1
1
输出：1
1
2
3
4

PAT 中的 测试点2 应该就是这种形式的。

因为没有边，所以在邻接表往并查集unity的过程中，在判断链表到达结尾时，会有问题。可能会在最后一个结点（tmp.next==0）时，加上一个 j->0 的边，然而很显然 0 这个结点是不存在的。

所以要在判断的时候要加上 tmp.v>0

cin>>a;
init();
for(int j=1; j<=n; j++) {
	if(j==a) {
		continue;
	} else {
		tmp=edge[head[j]];
		while(tmp.next!=0) {
			if(tmp.v!=a&&tmp.v>0) {
				unity(j,tmp.v);
			}
			tmp=edge[tmp.next];
		}
		if(tmp.v!=a&&tmp.v>0) {
			unity(j,tmp.v);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.5 邻接表版本 - AC 代码

#include
#include
#include
#include
using namespace std;
int n,m,k;
int fa[101000];
int head[101000],vis[101000],dis[101000],cnt;
set<int> con;

struct Edge {
	int v,w,next;
} edge[10001000],tmp;

void addEdge(int u, int v,int w) {
	edge[++cnt].v=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt;
}

void init() { //并查集初始化
	for(int i=1; i<=n; i++) {
		fa[i]=i;
	}
}

int find(int x) { //并查集查找
	if(x != fa[x]) { //当x不等于它的爸爸时(当它是祖先时，它没有爸爸)
		fa[x] = find(fa[x]);//继续找他的爸爸的爸爸
	}
	return fa[x];//返回祖先
}//查找


void unity(int x, int y) { //并查集合并
	int r1 = find(x);//找到x的祖先
	int r2 = find(y);//找到y的祖先
	if(r1!=r2) {
		fa[r1] = r2;//祖先和祖先结为父子(谁是父亲谁是儿子都可以)
	}
}//合并


int main() {
	cin>>n>>m>>k;


	cnt=0;
	int a,b;
	for(int i=0; i<m; i++) {
		cin>>a>>b;
		addEdge(a,b,1);
		addEdge(b,a,1);
	}

	for(int i=0; i<k; i++) {
cin>>a;
init();
for(int j=1; j<=n; j++) {
	if(j==a) {
		continue;
	} else {
		tmp=edge[head[j]];
		while(tmp.next!=0) {
			if(tmp.v!=a&&tmp.v>0) {
				unity(j,tmp.v);
			}
			tmp=edge[tmp.next];
		}
		if(tmp.v!=a&&tmp.v>0) {
			unity(j,tmp.v);
		}
	}
}

		con.clear();
		for(int j=1; j<=n; j++) {
			if(j!=a) {
				b=find(j);
				con.insert(b);
			}
		}
		cout<<con.size()-1<<endl;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86