答案

（1）凸函数(Convex function)和非凸函数(Convave function)
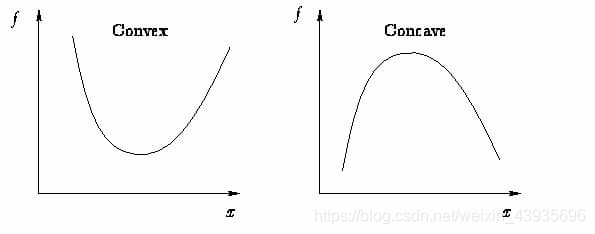
通常把函数分为凸函数和非凸函数。凸函数的几何意义在于，定义域中任意两点连线组成的线段都在这两点的函数曲线（面）上方。如图所示。凸函数是有且只有全局最优解的，而非凸函数可能有多个局部最优解。

（2）凸函数判定方法：

• 对于一元函数f(x)，首先必须定义域是凸集，其次通过其二阶导数f′′(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0 ，则f(x)是凸函数。
• 对于多元函数f(X)，首先必须定义域是凸集，其次通过其黑塞(Hessian)矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)凸函数。

扩展

（1）凸优化
在最小化（最大化）的优化要求下，目标函数是凸函数且约束条件所形成的可行域集合是一个凸集的优化方法，因此凸优化的判定条件有两个

• 函数定义域是凸集
• 目标函数是凸函数

（2）经典凸优化问题

• Least squares（最小二乘法，常用，目标：线性关系；限制条件：线性关系）
• Convex quadratic minimization with linear constraints（线性约束条件下的二次规划问题，常用，目标：平方关系；限制条件：线性关系）
• Linear programming（线性规划）
• Quadratic minimization with convex quadratic constraints(具有凸二次约束的二次最小化)
• Conic optimization(圆锥优化)
• Geometric programming(几何规划)
• Second order cone programming(二阶锥规划)
• Semidefinite programming(半定规划)
• Entropy maximization with appropriate constraints(具有适当约束的熵最大化)