【数据结构复习】第六章图

(一)图的逻辑结构

1.图的定义
（1）图中常将数据元素称为顶点。
（2）图由顶点的有穷非空集合和顶点之间的边的集合组成，记为：G = (V,E)。

（3）G表示一个图，V是顶点集合，E是顶点之间边的集合。

例：

顶点集合V = {v0，v1，v2，v3，v4}，边的集合{(v0,v1),(v0,v3),(v1,v2),(v1,v4),(v2,v3),(v2,v4)}

（4）有向、无向
顶点vi，vj之间的边没有方向叫无向边，用无序偶对(vi，vj)表示。
顶点vi，vj之间有方向叫边为有向边(也称为)，用有序偶对表示。

顶点之间都是无向边，则该图称为无向图。

顶点之间都是有向边，则该图称为有向图。

（5）权、带权图(网图)
对边赋予有意义的数值量，可以由具体含义。
边上带权的图称为带权图或网图。

无向网图

有向网图

2.图的基本术语

（1）邻接
无向图中，两顶点间存在边(vi，vj)，则vi，vj互为邻接点，同时称边依附于顶点vi，vj。
有向图中，两顶点vi，vj，若存在弧，则称顶点vi邻接到顶点vj，顶点vj邻接自顶点vi，同时称弧依附于顶点vi和顶点vj。

V1的邻接点： V2 、V3
V3的邻接点： V4

（2）顶点的度、入度、出度
无向图中顶点v的度是依附于该顶点的边数。记为：TD(v)

有向图中，顶点v的入度是指以该顶点为弧头的弧的数目，记为：ID (v)
有向图中，顶点v的出度是指以该顶点为弧尾的弧的数目，记为：OD (v)

（3）无向完全图、有向完全图

无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。
含有n个顶点的无向完全图有n×(n-1)/2条边

有向图中，如果任意两个顶点之间都存在方向相反的两条弧，则称该图为有向完全图。
含有n个顶点的有向完全图有n×(n-1)条边。

（4）稠密图、稀疏图
变数少——稀疏图，边数多——稠密图。

（5）路径、路径长度、回路
在无向图G=(V, E)中，从顶点vp到顶点vq之间的路径是一个顶点序列(vp=vi0,vi1,vi2, …, vim=vq)

路径上边的数目叫路径长度。

例：
V1 到V4的路径：
V1 V4（长度：8）
V1 V2 V3 V4（长度：7）
V1 V2 V5V3 V4（长度：15）

第一个顶点和最后一个顶点相同的路径叫回路。

（6）简单路径、简单回路
顶点不重复出现的路径叫简单路径。
除第一个顶点和最后一个顶点之外，不重复出现的回路叫简单回路。

（7）子图
若图G=（V，E），G’=（V’，E’），如果V’⊆V且E’ ⊆ E ，则称图G’是G的子图。

一个图可以有多个子图。

（8）连通图、连通分量
从一个顶点vi到另一个顶点vj(i≠j)有路径，则称顶点vi和vj是连通的，任意两个顶点都是连通的，则称该图是连通图。
连通分量：非连通图的极大连通子图称为连通分量。

例：求连通分量

此图有两个连通分量

（9）强连通图、强连通分量
有向图中，对图中任意一对顶点vi和vj(i≠j)，若从顶点vi到顶点vj和从顶点vj到顶点vi均有路径，则称该有向图是强连通图。

强连通分量：非强连通图的极大强连通子图。

例：求强连通分量

此图有两个强连通分量

(二)图的遍历操作

图的遍历操作是从图中某顶点出发，对图中所有顶点访问一次且仅访问一次。

需要解决的问题：
a。如何选取起始顶点。

将顶点进行编号，从编号小的顶点开始，编号不唯一，采用一维数组存储顶点信息

b。从某顶点出发可能到达不了所有顶点，如非连通分量。

多次重复从某一顶点出发进行图的遍历(一个个遍历)。

c。图中可能存在回路，某些顶点可能被重复访问，如何避免因回路陷入死循环。

设置访问标志数组visited[n](n为顶点个数)区分顶点是否访问，初值为0表示未访问，若某顶点i已被访问，访问标志visited[i]的值置为1。

d。一个顶点可与多个顶点相邻接，如何选取下一个要访问的顶点。

有深度优先遍历和广度优先遍历对有向、无向图都适用。

1.深度优先遍历(类似于树的前序遍历)

基本思想：
输入：顶点编号v
(1)访问顶点v，修改标志visited[v] = 1
(2)从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历。(w = 顶点v的第一个邻接点)
(3)重复上两步，直到图中所有和v有路相通的顶点都被访问到。
while（w存在）
a。if（w未被访问）从顶点w出发递归执行该算法
b。w = 顶点v的下一个邻接点

例一：


例二：

2.深度优先遍历的入栈出栈序列

（1）深一层递归V1、V2、V4、V5入栈

（2）递归返回5出栈8入栈

（3）递归返回8出栈，递归返回到V1

（4）V2、V4出栈，深一层递归V3、V6、V7入栈

（5）最后递归返回，V1、V3、V6、V7依次出栈。

3.广度优先遍历(类似于树的层序遍历)

基本思想：
(1) 访问顶点v；
(2) 依次访问v的各个未被访问的邻接点v1, v2, …, vk；
(3) 分别从v1，v2，…，vk出发依次访问和v有路径相通且路径长度为1、2的顶点，为了使"先被访问顶点的邻接点”先于“后被访问顶点的邻接点"被访问，设置队列存储已被访问的顶点。

例一：


例二：

4.广度优先遍历的入队出队序列

（1）广度优先遍历，V1入队

（2）V1出队，V2、V3入队

（3）V2继续向下遍历，V2出队，V4、V5入队

（4）V3继续向下遍历，V3出队，V6、V7入队

（5）V4继续向下遍历，V4出队，V8入队

（6）所有顶点都遍历到了，剩下的V5、V6、V7、V8出队。

(三)图的存储结构及实现

两种存储结构——邻接矩阵、邻接表。

1.邻接矩阵存储结构
图的邻接矩阵存储(数组表示法)，用一维数组存储图的顶点。
二维数组存储图的边(各顶点之间邻接关系)，存储邻接关系的二维数组叫邻接矩阵。

设图G＝(V，E)有n个顶点，则邻接矩阵是一个n×n的方阵，定义为：

无向图的邻接矩阵一定是对称矩阵，有向图不一定是对称矩阵。
（1）无向图的邻接矩阵

a。如何求顶点i的度：邻接矩阵第i行或i列的非0元素的个数。

b。如何判断顶点 i 和 j 之间是否存在边：测试邻接矩阵中相应位置的元素arc[i][j]是否为1，是1则表示i、j之间存在边。

c。如何求顶点 i 的所有邻接点：将数组中第 i 行元素扫描一遍，若arc[i][j]为1的，则顶点 j 为顶点 i 的邻接点。

（2）有向图的邻接矩阵

a。如何求顶点 i 的出度：
邻接矩阵的第 i 行元素之和。

b。如何求顶点 i 的入度：
邻接矩阵的第 i 列元素之和。

c。如何判断从顶点 i 到顶点 j 是否存在边：
测试邻接矩阵中相应位置的元素arc[i][j]是否为1。

设G是网图，则邻接矩阵可定义为：

其中Wij表示边(vi，vj)或弧上的权值，无穷表示计算机允许的大于所有边上的权值的数。

2.邻接矩阵的实现

（1）邻接矩阵存储类定义

const int MaxSize = 10;             //图中最多顶点个数
template <typename DataType>
class MGraph 
{ 
public:
    MGraph(DataType a[ ], int n, int e);
    ~MGraph( )
    void DFTraverse(int v);         //深度优先遍历图
    void BFTraverse(int v);         //广度优先遍历图
private:
    DataType vertex[MaxSize];       //存放图中顶点的数组
    int arc[MaxSize][MaxSize];      //存放图中边的数组
    int vertexNum,edgeNum;          //图中的顶点数和边数
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

（2）构造函数

template <typename DataType>
MGraph::MGraph(DataType a[ ], int n, int e)
{
    int i,j,k;
    vertexNum = n;
    edgeNum = e;
    for (i = 0; i < vertexNum; i++)         //存储顶点
        vertex[i] = a[i];
    for (i = 0; i < vertexNum; i++)         //初始化邻接矩阵
        for (j = 0; j < vertexNum; j++)
            edge[i][j] = 0;
    for (k = 0; k < edgeNum; k++)
    {                                       //依次输入每一条边
        cin >> i >> j;                      //边依附的两个顶点的序号
        edge[i][j] = 1;
        edge[j][i] = 1;                     //置有边标志
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

（3）析构函数
析构函数为空，无需销毁

（4）深度优先遍历

template <typename DataType>
void MGraph<DataType>::DFTraverse(int v)
{
    cout << vertex[v];
    visited [v] = 1;                            //找顶点v的邻接点，v所在行等于1的列
    for (j = 0; j < vertexNum; j++)
        if (arc[v][j] == 1 && visited[j] == 0)  //visited = 0未被访问的点
            DFTraverse( j );
}
1
2
3
4
5
6
7
8
9

（5）广度优先遍历

template <typename DataType>
void MGraph<DataType>::BFTraverse(int v)
{
    int w,j,Q[MaxSize];
    front = rear = -1;          //初始化队列，假设采用顺序队列且不会发生溢出
    cout << vertex[v];
    visited[v] = 1;
    Q[++rear] = v;              //被访问顶点入队
    while (front != rear)      //队列非空
    {
        w = Q[++front];        //将队头元素出队
        for (j = 0; j < vertexNum; j++)
            if (arc[v][j] == 1 && visited[j] == 0 )
            {
                cout << vertex[j];
                visited[j] = 1;
                Q[++rear] = j;
            }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3.邻接表
顺序存储与连接存储结合，类似树的孩子表示法。

1.邻接表的存储结构
对于图的每个顶点vi，将所有邻接于vi的顶点链成一个单链表，称为顶点vi的边表（对于有向图则称为出边表）。
所有边表的头指针和存储顶点信息的一维数组构成了顶点表。

（1）结点结构：

vertex：数据域，存放顶点信息。
firstedge：指针域，指向边表中第一个结点。
adjvex：邻接点域，边的终点在顶点表中的下标。
next：指针域，指向边表中的下一个结点
注：对于网图，边表还需增设info域存储边上信息(如权值)。

顶点表结点和边表结点的结构体定义：

struct EdgeNode             //定义边表结点
{
    int adjvex;             //邻接域
    EdgeNode *next;
};
template <typename DataType>
struct VertexNode           //定义顶点表结点
{
    DataType vertex;
    EdgeNode *firstEdge;
};
1
2
3
4
5
6
7
8
9
10
11

（2）无向图的邻接表存储示意图：

a。边表中的结点表示什么？
每个结点对应图中的一条边。

b。如何求顶点 i 的度？
顶点i的边表中结点的个数。

c。如何判断顶点 i 和顶点 j之间是否存在边?
测试顶点 i 的边表中是否存在终点为 j 的结点。

（3）有向图的邻接表

a。如何求顶点 i 的出度？
顶点 i 的出边表中结点的个数。

b。如何求顶点 i 的入度？
各顶点的出边表中以顶点 i 为终点的结点个数。

c。如何求顶点 i 的所有邻接点？
遍历顶点 i 的边表，该边表中的所有终点都是顶点 i 的邻接点。

（4）网图的邻接表

4.邻接表的实现

（1）邻接表类定义

const int MaxSize = 10; //图的最大顶点数
template <typename DataType>
class ALGraph 
{ 
public:
    ALGraph(DataType a[ ], int n, int e);
    ~ALGraph;
    void DFTraverse(int v);
    void BFTraverse(int v);
private:
    VertexNode adjlist[MaxSize];
    int vertexNum, edgeNum;
};
1
2
3
4
5
6
7
8
9
10
11
12
13

（2）构造函数

template <typename DataType>
ALGraph<DataType>::ALGraph(DataType a[ ], int n, int e)
{
    int i,j,k;
    EdgeNode *s = nullptr;
    vertexNum = n; edgeNum = e;         //n个顶点，e个边
    for (i = 0; i < vertexNum; i++)     //输入顶点信息，初始化边表
    {
        adjlist[i].vertex = a[i];
        adjlist[i].firstedge = NULL;
    }
    for (k = 0; k < edgeNum; k++)        //输入边的信息存储在边表中
    {
        cin >> i >> j;                   //输入边所依附的两个顶点编号
        s = new EdgeNode;
        s->adjvex = j;                   //生成边表结点s
        s->next = adjlist[i].firstedge;  //将结点s插入表头
        adjlist[i].firstedge = s;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

（3）析构函数

template <typename DataType>
ALGraph<DataType>::~ALGraph()
{
    EdgeNode *p = nullptr,*q = nullptr;
    for (int i = 0;i < vertexNum;i++)
    {
        p = q = adjlist[i].firstEdge;
        while (p!=nullptr)
        {
            p = p->next;
            delete q;q = p;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

（4）深度优先遍历

template <typename DataType>
void ALGraph<DataType>::DFTraverse(int v)
{
    int j;
    EdgeNode *p = nullptr;
    cout << adjlist[v].vertex;
    visited[v] = 1;
    p = adjlist[v].firstedge;       //工作指针p指向顶点v的边表
    while (p != NULL)               //依次搜索顶点v的邻接点j
    {
        j = p->adjvex;
        if (visited[j] == 0) DFTraverse(j);
        p = p->next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

（5）广度优先遍历

template <typename DataType>
void ALGraph<DataType>::BFTraverse(int v)
{
    int w,j,Q[MaxSize];
    front = rear = -1;
    EdgeNode *p = nullptr;
    cout << adjlist[v].vertex;
    visited[v] = 1;
    Q[++rear] = v;                      //被访问顶点入队
    while(front != rear)               //当队列非空时
    {
        v = Q[++front];
        p = adjlist[v].firstedge;       //工作指针p指向顶点v的边表
        while(p != NULL)
        {
            j = p->adjvex;
            if(visited[j] == 0) {
                cout << adjlist[j].vertex; visited[j] = 1;
                Q[++rear] = j;
            }
            p = p->next;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

5.邻接矩阵和邻接表的比较

（1）空间性能
邻接矩阵是nxn的矩阵，空间代价是O(n^2)。
邻接表，邻接表空间代价与图的边数和顶点有关空间代价为O(n+e)。
邻接矩阵存储所有可能的边，图越稠密，邻接矩阵空间效率越高。
稀疏矩阵采用邻接表。

（2）时间性能比较
使用邻接表，只需检查此顶点的边表，平均查找时间O(e/n)。
使用邻接矩阵，需检查所有可能的边，需要查找O(n)次。

(四)最小生成树

1.相关概念

（1）连通图的生成树：是包含图中全部顶点的极小连通子图。

（2）生成树的特点：
♣ 生成树的顶点个数与图的顶点个数相同。
♣ 生成树是图的极小连通子图。
♣ 一个有n个顶点的连通图的生成树有n-1条边。
♣ 生成树中任意两个顶点间的路径是唯一的。
♣ 在生成树中再加一条边必然形成回路。

（3）生成树的代价：设G=（V，E）是一个无向连通网，生成树上各边的权值之和称为该生成树的代价。

（4）最小生成树：所有生成树中代价最小的称为最小生成树。

例：图中为连通图G，和生成树1、生成树2。

2.Prim算法

基本思想：
设G=(V, E)是具有n个顶点的连通网，T=(U, TE)是G的最小生成树， T的初始状态为U={u（u0∈V），TE={ }，重复执行下述操作：
在所有u∈U，v∈V-U的边中找一条代价最小的边(u, v)并入集合TE，同时v并入U，直至U=V。

例： Prim算法构造最小生成树过程。

（1）cost中有从顶点A开始到所有顶点的路径，A进入U，三条路径可走，选择cost最少的(A,F)19。

（2）F进入U，到剩下未到达的顶点有AB和F的三条路径可走，选择cost最少的FC

（3）C进入U，到剩下未到达的顶点有CD、AB、FE三条路径，选择cost最少的(CD)17

（4）D进入U，选择cost较小的(F,E)

（5）进入U选择剩下的BE

（6）所有顶点进入，最小生成树构造完成

prim算法的存储结构
a。图的存储结构：由于算法执行过程需要不断的读取任意两顶点之间的权值，所以采用邻接存储。

b。候选最短边集：设数组adjvex[n]和lowcost[n] 分别表示 最短边的邻接点和权值。

初始时，U = {v}，lowcost[v] = 0表示顶点v加入集合U。

数组元素adjvex[i] = v，lowcost[j] = 边(v，i)的权值（1<=i<=n-1）。

在数组lowcost[n]中选取最小的权值lowcost[j]，顶点j从集合V-U进入集合U后，最短边集变化，根据下式adjvex[n]和lowcost[n]更新，将lowcost置为0，表示将顶点j加入集合U中。

locost[i] = min{lowcost[i]，边(i，j)的权值}
adjvex[i] = j(如果边(i，j)的权值

下表为无向联通网图构造最小生成树数组adjvex和lowcost及集合U的变化

void Prim(int v)                    //从顶点v出发
{
    int i,j,k;
    int adjvex[MaxSize],lowcost[MaxSize];
    for (i = 0;i < vertexNum;i++)   //初始化辅助数组
    {
        lowcost[i] = edge[v][j]; adjvex[i] = v;
    }
    lowcost[v] = 0;                 //将顶点v加入集合U
    for (k = 1;k <vertexNum;k++)    //迭代n-1次
    {
        j = MinEdge(lowcost,vertexNum);     //寻找最短边
        cout<<j<<adjvex[j]<<lowcost[j]<<endl;
        lowcost[j] = 0;                     //顶点j加入集合U
        for (i = 0;i < vertexNum;i++)       //调整辅助数组
            if (edge[i][j]<lowcost[i])
        {
                lowcost[i] = edge[i][j]; adjvex[i] = j;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

3.Kruskal算法

Kruskal算法的关键是：判断被考察边的两个顶点是否位于两个连通分量。

基本思想：
设无向连通网为G＝(V, E)，令G的最小生成树为T＝(U, TE)，其初态为U＝V，TE＝{ }，图G中每个顶点自成一个连通分量。
图G中每个顶点自成一个连通分量。按照边的权值由小到大的顺序，在G的边集E中选择代价最小的边。

•若该边依附的顶点属于T中不同的连通分量上，则将此边作为最小生成树的边加入到T中，
•否则舍去此边而选择下一条代价最小的边。
•依此类推，直至所有顶点都在同一连通分量上。此连通分量便为G的一棵最小生成树。

例： Kruskal算法构造最小生成树过程。

（1）构造开始，每个顶点是一个连通分量。

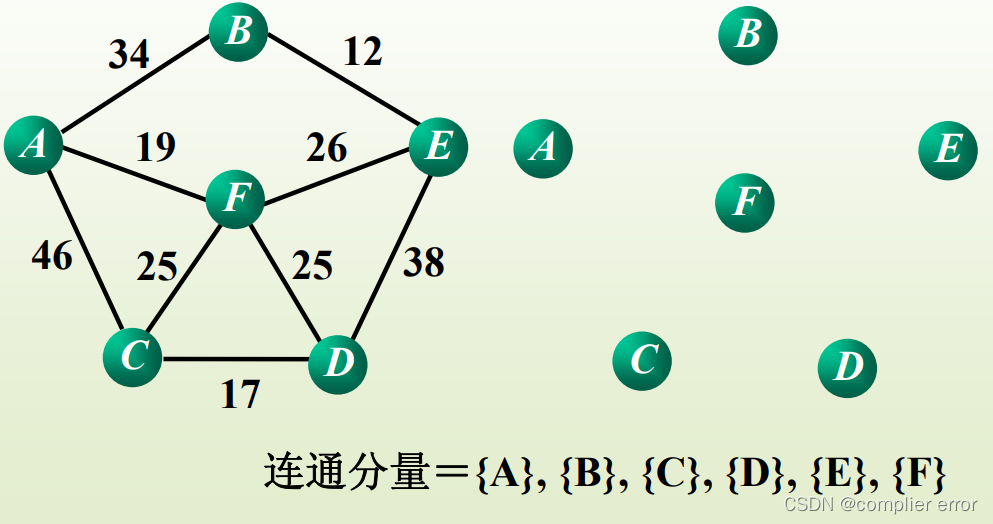
（2）选择权值最小的边BE，BE放一块。

（3）继续选择最小权值的边，AF，将AF放一块。

（4）继续选择最小的，CD放一块。

（5）AF、CD之间选择权值最小的边AFCD放一块。

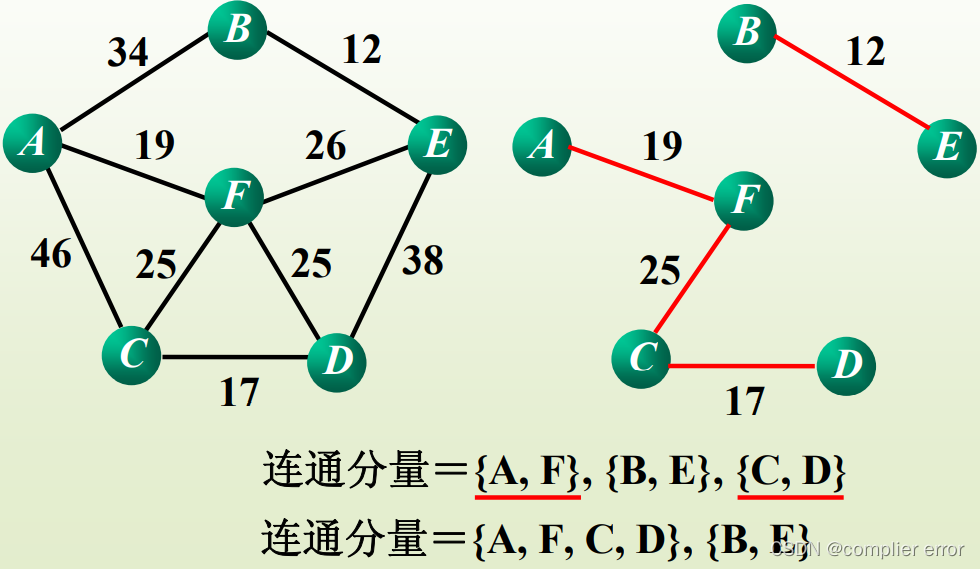
（6）AFCD和BE之间选择权值最小的边，AFCD和BE放一块。此时所有顶点位于一个连通分量，结束Kruskal算法。

Kruskal算法的存储结构
a。采用边集数组存储，为了提高查找最短边的速度，将边集数组的边按权值排序。
边集数组的结构体定义

struct EdgeType					//定义边集数组的元素类型
{
	int from，to，weight;		//假设权值为整数
}
1
2
3
4

b。连通分量所在集合涉及集合的查找合并等操作，采用并查集实现。
即将集合中的元素组织成树的形式，合并两个集合即将一个集合的根结点作为另一个的孩子。

下图为并查集合并过程

图的边集数组存储

const int MaxVertex = 10;                   //图中最多点数
const int MaxEdge = 100;                    //图中最多边数
template<typename DataType>

class EdgeGraph
{
public:
    EdgeGraph(DataType a[],int n,int e)
    ~EdgeGraph();
    void Kruskal();                         //Kruskal算法生成最小生成树

private:
    int FindRoot(int parent[],int v);      //求顶点v所在的集合的根
    DataType vertex(MaxVertex);             //存储顶点的一维数组
    EdgeType edge[MaxEdge];                 //存储边的边集数组
    int vertexNum,edgeNum;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Kruskal算法成员函数定义

void Kruskal()
{
    int num = 0,i,vex1,vex2;
    int parent[vertexNum];          //双亲表示法存储并查表
    for (i = 0;i < vertexNum;i++)
        parent[i] = -1;             //初始化n个连通分量

    for (num = 0,i = 0;num < vertexNum-1;i++)       //依次考察最短的边
    {
        vex1 = FindRoot(parent,edge[i].from);
        vex2 = FindRoot(parent,edge[i].to);
        if (vex1 ！=vex2){                          //位于不同的集合
            cout<<"("<<edge[i].from<<","edge[i].to<<")"<<edge[i].weight;
            parent[vex2] = vex1;                    //合并集合
            num++;
        }
    }
}

int FindRoot(int parent[],int v)                   //求顶点v所在集合的根
{
    int t = v;
    while (parent[t]>-1)                           //求顶点t的双亲一直到根结点
        t = parent[t];
    return t;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

两种算法的比较：
Prim算法：时间复杂度为O(n^2)，适用范围：稠密图。
Kruskal算法：时间复杂度为O(eloge)，适用范围：稀疏图。

(五)最短路径

a。非网图中，最短路径指两顶点之间边数最少的路径。

b。在网图中值两顶点之间权值最小的路径。

c。路径上第一个顶点称为源点，最后一个顶点称为终点。

1.Dijkstra算法（最短路径问题，重点是画表）
Dijkstra用于求单源点的最短路径问题，输出的是选取的开始顶点v到其他顶点的最短路径。
问题描述： 给定带权有向图G＝(V, E)和源点v∈V，求从v到G中其余各顶点的最短路径。

Dijkstra算法按路径长度递增的次序产生最短路径，黄色顶点表示生长点，红边表示已求得最短路径。

（1）初始待定路径表，得到生长点v1。

（2）更新待定路径表，得到生长点v3。

（3）更新待定路径表，得到生长点v2。

（4）更新待定路径表得到生长点v4结束Dijkstra算法

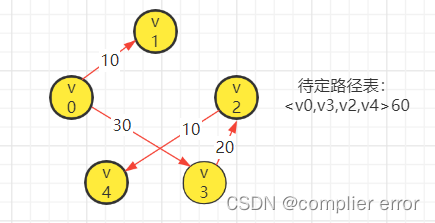
Dijkstra算法执行过程中各参量变化过程

存储结构：
a。需要快速取得边上的权值，所以选择邻接矩阵存储。

b。辅助数组dist[n]，元素dist[i]表示当前找到的从源点v到vi的最短路径。
若v到vi之间有弧则dist[i]为弧上的权值，若v到vi无弧则dist[i]为∞。
若求得终点为vk，则根据下式进行迭代：
dist[i] = min{ dist[i],dist[k]+edge[k][i] } （0<=i<=n-1）

c。辅助数组path[n]，path[i]是一个字符串，表示从源点到终点vi的路径。
若v到vi之间有弧则path[i]为" vvi ",否则置path[i]为空串。

d。集合S，若顶点vk的最短路径已求出则dist[k]置为0，即数组dist[n]中值为0对应的是顶点下。

函数定义

void Dijkstra(int v)                    //从源点出发
{
    int i,k,num,dist[MaxSize];
    string path[MaxSize];
    for (i = 0;i < vertexNum;i++)       //初始化数组dist和path
    {
        dist[i] = edge[v][i];
        if (dist[i] != 100)             //假设100为边上权的最大值
            path[i] = vertex[v] + vertex[i];        //+为字符串的连接字符
        else path[i] = "";
    }
    for (num = 1;num < vertexNum;num++)
    {
        k = Min(dist,vertexNum);                    //在dist数组中找到最小下标并返回数组下标
        cout <<path{[k]<<dist[k];
        for (i = 0;i < vertexNum;i++)               //修改数组dist和path
        if (dist[i]>dist[k] + edge[k][i]){
            dist[i] = dist[k] + edge[k][i];
            path[i] = path[k] + vertex[i];
        }
        dist[k] = 0;                                //将顶点k加入到集合S中
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

2.Floyd算法（最短路径问题）

给定带权有向图G = (V，E)，对任意顶点vi和vj（i！=j）求顶点vi到vj的最短路径。

基本思想：
若vi 到vj 有弧（若不存在vi到vj的弧，则权值为∞），则从vi 到vj 存在一条长度为arcs[i][j]的路径，该路径不一定是最短路径，尚需进行n次试探：

如图：
在路径上增加一个顶点v0 ，考虑路径(vi , v0, vj )是否存在(即判别弧(vi , v0 )和(v0 , vj )是否存在)。

a。首先比较vivj和viv0vj的路径长度，取长度较短者作为vi到vj之间编号不大于0的最短路径（谁短谁是0）

b。再次比较，在路径上再增加一个顶点v1和已经得到的编号不大于0的最短路径进行比较，取长度短的作为中间顶点编号不大于1的最短路径（与0比谁短谁是1）

c。以此类推，vi……vk和vk……vj分别是从vi到vk和vk到vj中间顶点编号不大于k-1的最短路径，将
vi……vk……vj与顶点编号不大于k-1的进行比较，短的是顶点编号不大于k的最短路径。n次比较后得到的是vi到vj的最短路径。

Floyd算法执行过程中，数组dist和path的变化。

void Floyd()
{
    int i,j,k,dist[MaxSize][MaxSize];
    string path[MaxSize][MaxSize];
    for (i = 0; i < vertexNum; i++)                       //初始化矩阵dist和path
        for (j = 0; j < vertexNum; j++)
        {
            dist[i][j] = edge[i][j];
            if (dist[i][j] != 100)                        //假设100为权的最大值
                path[i][j] = vertex[i] + vertex[j];
            else path[i][j] = "";
        }
    for (k = 0; k < vertexNum; k++)                      //进行n次迭代
        for (i = 0; i < vertexNum; i++)
            for (j = 0; j < vertexNum; j++)
                if (dist[i][k] + dist[k][j] < dist[i][j])
                {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    path[i][j] = path[i][k] + path[k][j];
                }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

(六)有向无环图及其应用

1.AOV网与拓扑排序
在一个表示工程的有向图中：用顶点表示活动，用弧表示活动之间的优先关系，称这样的有向图为顶点表示活动的网，简称AOV网。

（1）AOV网特点
a。AOV网之间的弧表示活动之间存在某种制约关系。
b。AOV网中不能出现回路。
因此判断AOV网代表的工程能否顺利进行，即判断它是否存在回路。

（2）拓扑序列
设G=(V，E)是一个具有n个顶点的有向图，V中的顶点序列v1, v2, …, vn称为一个拓扑序列。
当且仅当满足下列条件：若从顶点vi到vj有一条路径，则在顶点序列中顶点vi必在顶点vj之前。拓扑排序：对一个有向图构造拓扑序列的过程称为拓扑排序。

（3）AOV网及拓扑序列

（4）AOV网进行拓扑排序的基本思想：
a。AOV网中选择一个没有前驱的顶点并输出。

b。从AOV网中删除该顶点，以及所有以该顶点为尾的弧。

c。重复以上两步，直到输出所有顶点。
AOV网中顶点全部被输出，说明AOV网中不存在回路。
AOV网中顶点未被全部输出，剩下顶点均不存在没有前驱结点的顶点，说明AOV网中存在回路。

2.拓扑排序的存储结构

（1）拓扑排序过程中，需要查找所有以某顶点为尾的弧，即需要找到该顶点的所有出边，因此图采用邻接表存储，另外在顶点表中加一个入度域，方便入度操作。

（2）AOV网及其邻接表

（3）查找没有前驱的顶点
为了避免每次查找时都遍历顶点表，设置一个栈，AOV网中入度为0的顶点都将其压栈。

void TopSort()
{
    int i,j,k,count = 0;                //累加器count初始化
    int S[MaxSize],top = -1;            //采用顺序栈并初始化
    EdgeNode *p = nullptr;
    for (i = 0;i < vertexNum;i++)v      //扫描顶点表
        if (adjlist[i].in==0) S[++top] = i;         //将入度为0的顶点压栈
    while (top!=-1)                                 //当栈中还有入度为0的顶点时
    {
        j = S[top--];                               //从栈中取出入度为0的顶点
        cout<<adjlist[j].vertex;
        count++;
        p = adjlist[j].firstEdge;                   //工作指针p初始化
        while (p!=nullptr)                         //扫描顶点表，找出顶点j的所有出边
        {
            k = p->adjvex;
            adjlist[k].in--;
            if (adjlist[k].in==0) S[++top] = k;     //将入度为0的顶点入栈
            p = p->next;
        }
    }
    if (count < vertexNum) cout<<"有回路";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3.关键路径AOE网

（1）定义
把工程计划表示为有向图，用顶点表示事件，弧表示活动，边上的权值表示活动的持续时间。这样边表示活动的网，简称AOE网。

AOE网中没有入边的顶点称为始点（或源点），没有出边的顶点称为终点（或汇点）。

关键活动：关键路径上的活动称为关键活动。

关键活动：关键路径上的活动称为关键活动。

（2）AOE网的性质
a。 只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；
b。只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

（3）
例：


a。从始点到终点的路径可能不止一条，只有各条路径上所有活动都完成了，整个工程才算完成。
b。完成整个工程所需的最短时间取决于从始点到终点的最长路径长度，即这条路径上所有活动的持续时间之和。这条路径长度最长的路径就叫做关键路径。

（4）找关键路径
要找关键路径首先要找出关键活动。

首先计算以下与关键活动有关的量：
a。事件的最早发生时间ve[k]
b。事件的最迟发生时间vl[k]
c。活动的最早开始时间e[i]
d。活动的最晚开始时间l[i]

最后计算各个活动的时间余量 l [k] - e [k] ,时间余量为0者即为关键活动。

（5）找出关键活动及关键路径需要定义如下数组





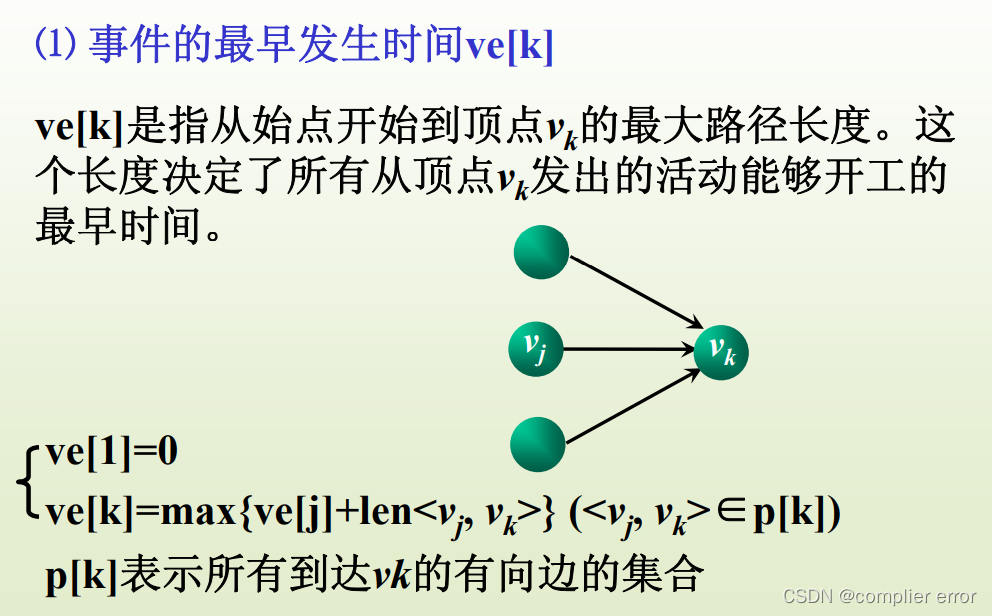
el [i] = ee [i]的活动就是关键活动。el [i] > ee[i]的活动不是关键活动，el [i] - ee[i]的值为活动的时间余量。关键活动确定后，关键活动所在路径就是关键路径。