数据结构与算法_排序算法_插入排序和希尔排序

插入排序

如果数据趋于有序，那么插入排序是所有排序算法中，效率最高的排序算法！
思想：假设第一个元素是已经排好序的；从第二趟开始依次从未排序的数据中选出一个，插入到已经排好序的数列中。从有序数列最后一个元素开始比较，如果当前待插入元素大于有序数列中的数据时候，就插入到被比较元素的后边，后边的元素依次向后移动。
在基础排序中，插入排序 > 冒泡排序&选择排序 不仅仅没有交换而且比较的次数少！
特点：从第二个元素开始，把前面的元素序列当作已经有序的，然后找合适的位置插入。
优点：插入排序是普通排序里面效率最高的排序算法，而且在数据越趋于有序的情况下，插入排序的效率是最高的。

void InsertSort1(int arr[], int size)
{
	for (int i = 1; i < size; i++) // 控制趟数,同时arr[i]是每趟中的无序元素
	{
		int val = arr[i];  // 每次比较时，将最后一个值拿出来了，所以可以进行下边的arr[j+1] = arr[j];
		int j = i - 1;   // 有序数组中最后一个元素
		for (; j >= 0; j--)   // 控制有序元素中，依次从后向前比较
		{
			if (arr[j] <= val)
			{
				break;
			}
			arr[j + 1] = arr[j];
		}
		arr[j + 1] = val;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

希尔排序

可以看成是插入排序的改进版；在写希尔排序时候，先写出插入排序；然后再改成希尔排序，将插入排序中添加一个循环。

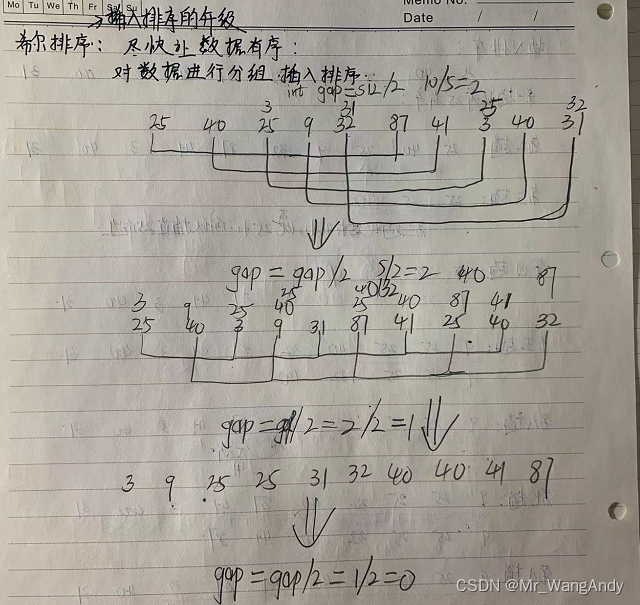
void ShellSort1(int arr[], int size)
{
	for (int gap = size / 2; gap > 0; gap /= 2) // 5 2 1 0 
	{
		for (int i = gap; i < size; i++) // O(n)  // 5 6 7 8 9 | 2 3 4 5 6 7 8 9 | 
		{
			int val = arr[i];
			int j = i - gap;  // 
			for (; j >= 0; j -= gap) // O(n)
			{
				if (arr[j] <= val)
				{
					break;
				}
				arr[j + gap] = arr[j];
			}
			arr[j + gap] = val;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

四种排序算法性能对比

插入排序的效率最好，尤其是在数据已经趋于有序的情况下，采用 插入排序效率最高 。
一般中等数据量的排序都用希尔排序，选择合适的增量序列，效率就已经不错了，如果数据量比较大，可以选择高级的排序算法，如快速排序。