1. 平衡二叉树定义、结构体

平衡二叉树 （Balanced Binary Tree），简称平衡树（AVL树），树上任一结点的左子树和右子树的高度之差不超过 1。

结点的平衡因子 = 左子树高 - 右子树高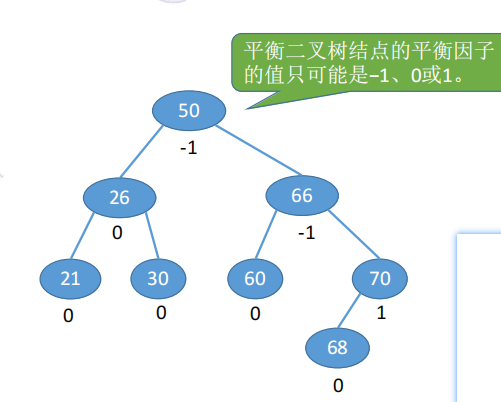

typedef struct AVLNode{
    int key;
    int balance;	//平衡因子
    struct AVLNode *lchild, *rchild;
}AVLNode, *AVLTree;
1
2
3
4
5

---

​

2. 平衡二叉树的插入

在二叉排序树中插入新结点后，如何保持平衡？

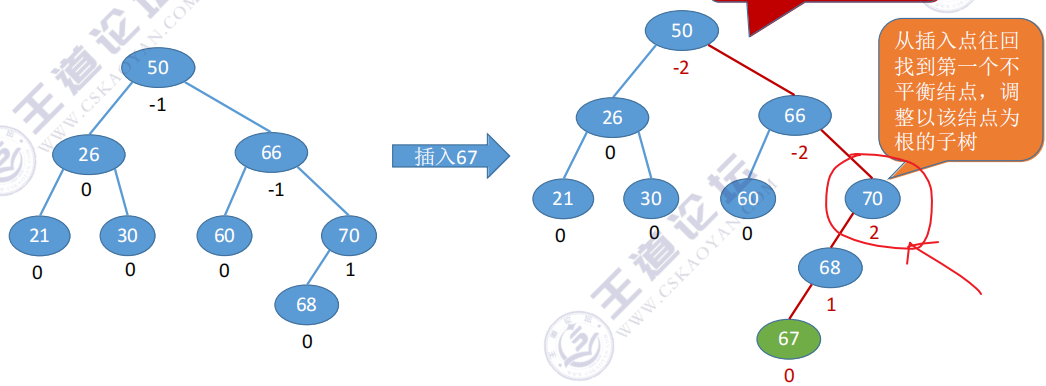
从插入点往回找到第一个不平衡结点，调整以该结点为根的子树；
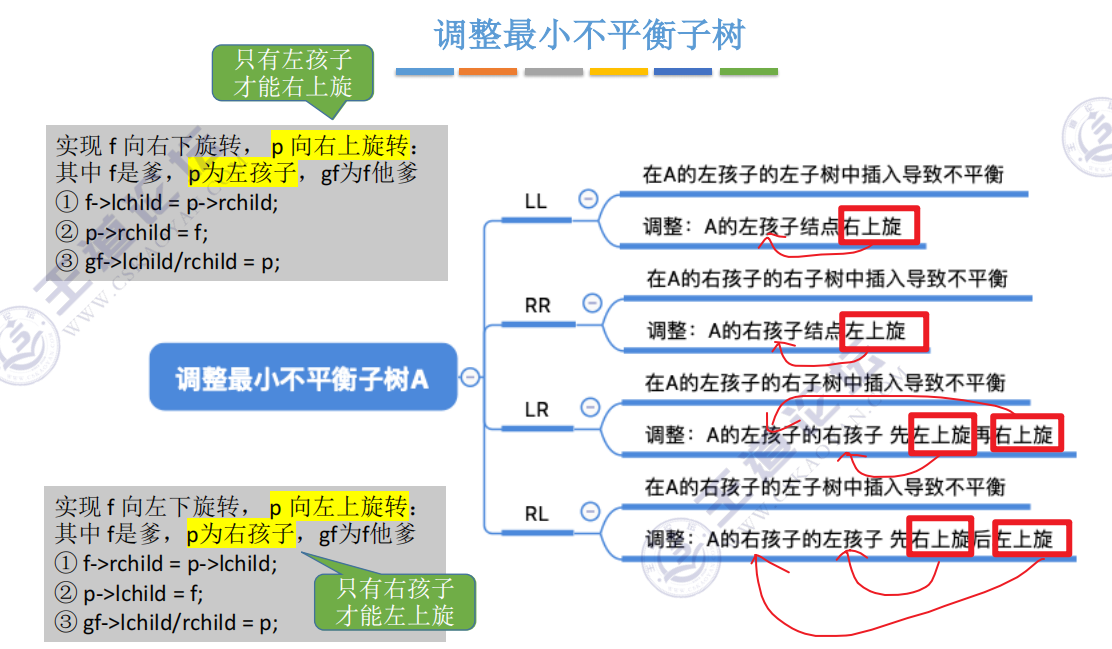
只要将最小不平衡子树调整平衡，则其他祖先结点都会恢复平衡。调整可分为以下四种情况：

1. LL：在A的左孩子的左子树中插入导致不平衡；
2. RR：在A的右孩子的右子树中插入导致不平衡；
3. LR：在A的左孩子的右子树中插入导致不平衡；
4. RL：在A的右孩子的左子树中插入导致不平衡。
   
   注：插入操作导致“最小不平衡子树”高度+1，经过调整后高度恢复

2.1 LL：在A的左孩子的左子树中插入【只右旋】

 
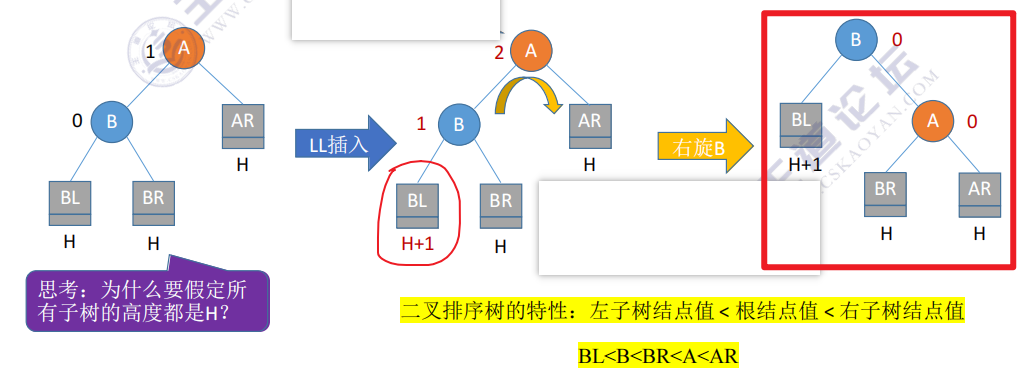
代码思路：
 

---

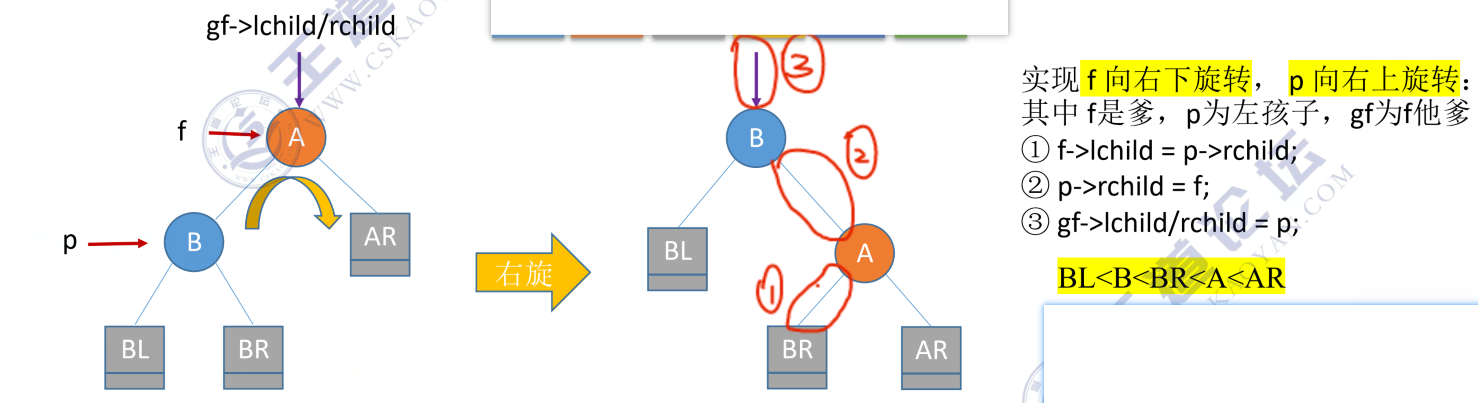
2.2 RR：在A的右孩子的右子树中插入【只左旋】

 
代码思路：
 

---

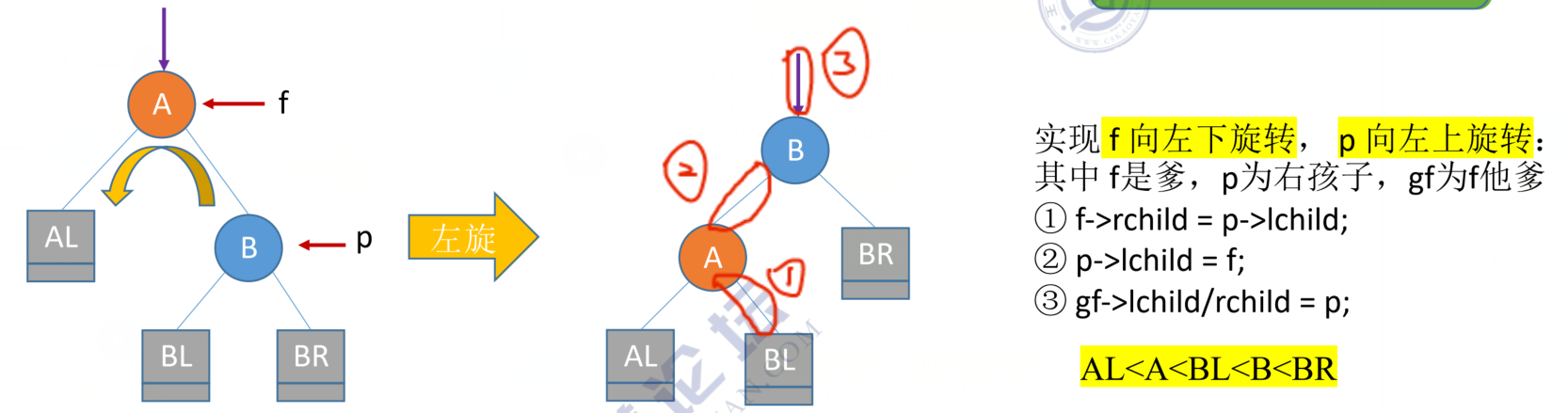
2.3 LR：在A的左孩子的右子树中插入【先右旋后左旋】

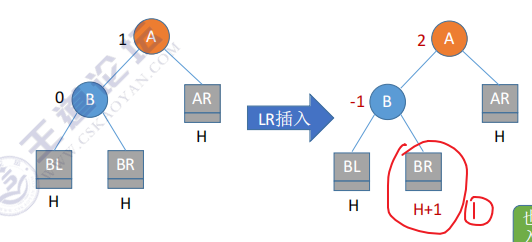
①中插入的位置可能是左子树，或右子树，分两种情况
C是在BR中的，只是把它从BR中拆出来了

---

2.4 RL：在A的右孩子的左子树中插入【先左旋后右旋】

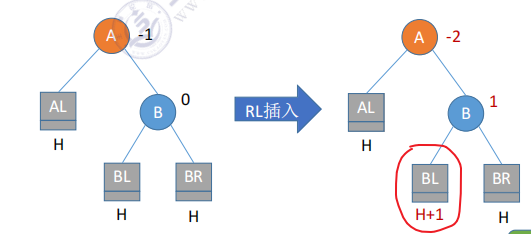
画红圈的地方——>插入的位置可能是左子树，或右子树，分两种情况
C是在BL中的，只是把它从BL中拆出来了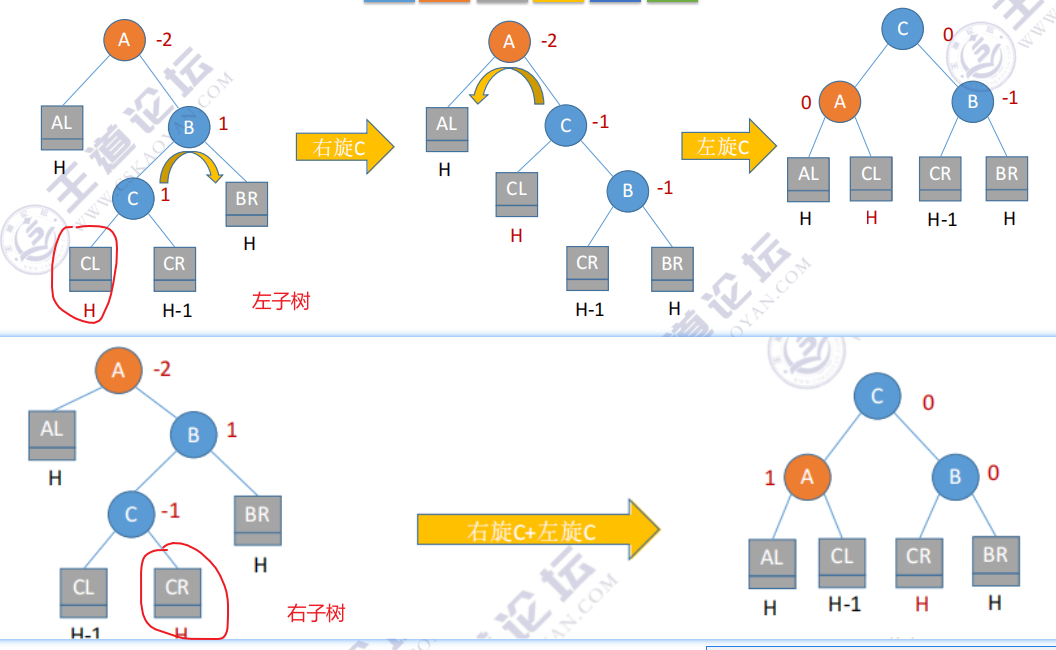

---

3. 插入练习题【必须看】

3.1 RR型插入

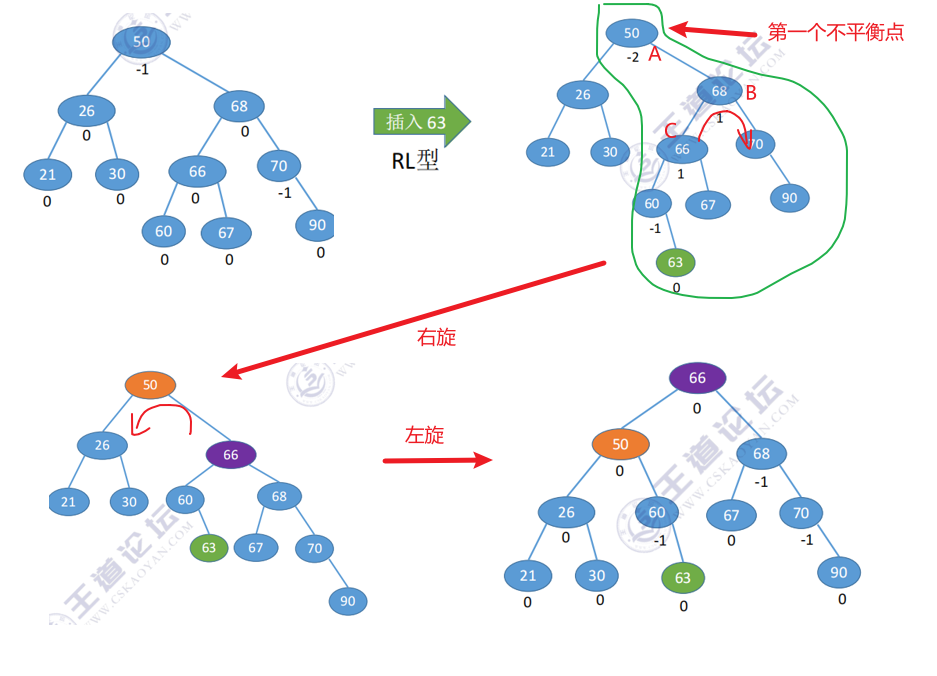
3.2 RL型插入

4. 查找效率分析

若树高为h，则最坏情况下，查找一个关键字最多需要对比 h 次，即查找操作的时间复杂度不可能超过 O(h)。