-
矩阵分解与应用(张贤达)day4
1、内积与范数
在讨论内积空间时,对向量的内积与范数作了比较简单的介绍。本节将对向量的内积与范数展开比较全面与深入的讨论,然后推广到矩阵的内积与范数。
1.1、向量的内积与范数
根据元素取值方式的不同,向量分为常数向量、函数向量和随机向量。常数向量是元素为常数的向量;函数向量是元素取某个变量的函数值的向量;而随机向量则是元素为随机变量的向量。虽然常数向量、函数向量和随机向量的内积定义公式有所不同,但是无论向量取何种形式,向量的内积和范数都必须服从一定的公理。
定义:令
 是复向量空间。函数
是复向量空间。函数 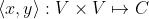 称为向量
称为向量 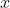 和
和 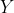 的内积,若对所有
的内积,若对所有 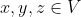 ,以下内积公理满足:
,以下内积公理满足:(1)
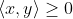 (非负性)
(非负性)(1a)
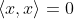 ,当且仅当
,当且仅当 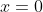 (正性)
(正性)(2)
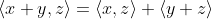 (可加性)
(可加性)(3)
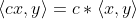 ,对所有复常数
,对所有复常数  成立 (齐次性)
成立 (齐次性)(4)
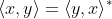 (Hermitian 性)
(Hermitian 性)式中,
 表示复数共轭。
表示复数共轭。定义:令
 是复向量空间。函数
是复向量空间。函数 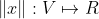 称为向量
称为向量 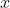 的范数,若对所有
的范数,若对所有 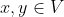 ,下面的范数公理成立:
,下面的范数公理成立:(1)
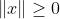 (非负性)
(非负性)(1a)
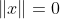 ,当且仅当
,当且仅当 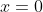 (正性)
(正性)(2)
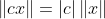 ,对所有复常数
,对所有复常数  成立 (齐次性)
成立 (齐次性)(3)
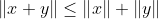 (三角不等式)
(三角不等式)上述公理是平面上的 Euclidean 长度的熟知性质。满足公理(1), (2), (3)但不一定满足公理(1a)的函数称为向量的半范数。
1、常数向量的内积与范数
两个
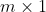 维常数向量
维常数向量 ![x = [x_{1}, x_{2}, \cdot \cdot \cdot , x_{m}]^{T}](https://1000bd.com/contentImg/2022/08/17/091435110.gif) 和
和 ![y = [y_{1}, y_{2}, \cdot \cdot \cdot , y_{m}]^{T}](https://1000bd.com/contentImg/2022/08/17/091436251.gif) 的内积(或叫点积)定义为
的内积(或叫点积)定义为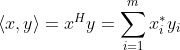
定义:两个向量之间的夹角定义为
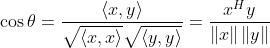
显然,若
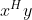 = 0,则
= 0,则 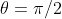 。此时,称常数向量
。此时,称常数向量 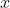 和
和 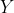 正交。因此,两个常数向量正交的数学定义如下。
正交。因此,两个常数向量正交的数学定义如下。定义:两个常数向量称为正交,若它们的内积等于零,即
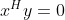 ,并记作
,并记作 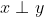 。
。由定义知,零向量
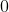 与同一空间的任何向量都正交。
与同一空间的任何向量都正交。 -
相关阅读:
第五十六周总结——后端接口开发及其生活总结
每天进步一点点 --- Guava
c语言 编程及答案
vue父组件如何向子组件传递数据?
GPU性能优化与模型训练概览
数据增强
tensorflow内存泄漏或模型只加载不运行
用于命名实体识别的模块化交互网络
内存学习(3):DRAM的基础存储结构(存储层级、读写过程,刷新与暂存)
单例模式只会懒汉饿汉?读完本篇让你面试疯狂加分
- 原文地址:https://blog.csdn.net/qq_44950283/article/details/126341918