leetcode 10. 正则表达式匹配（dp）

​
​

作者简介：C/C++ 、Golang 领域耕耘者，创作者
个人主页：作者主页
活动地址：CSDN21天学习挑战赛
题目来源： leetcode官网
如果感觉博主的文章还不错的话，还请关注➕ 、点赞👍 、收藏🧡三连支持一下博主哦~~~

💜 题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

示例1：

输入：s = “aa”, p = “a”
输出：false
解释：“a” 无法匹配 “aa” 整个字符串。

示例2：

输入：s = “aa”, p = “a*”
输出：true
解释：因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

示例3：

输入：s = “ab”, p = “."
输出：true
解释：".” 表示可匹配零个或多个（‘*’）任意字符（‘.’）。

🧡 算法分析

此题方法是用dp

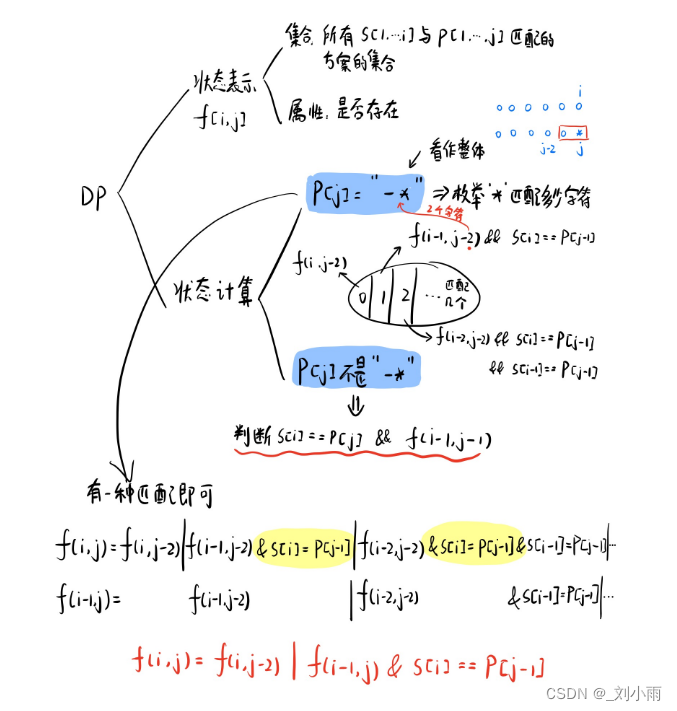
1. 设状态 f(i,j) 表示字符串 s 的前 i 个字符和字符串 p 的前 j 个字符能否匹配。这里假设 s 和 p 的下标均从 1 开始。初始时，f(0,0)=true。
2. 当p[j] != '*'时，f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
3. 当 p(j) == '*' 时，这时* 可以代表0个字符， 1个字符 …, 这时的状态转移方程为 f(i, j) = f(i, j - 2) || f(i-1, j -2) && s[i] == p[j - 1] || f(i - 2, j - 2) && s[i] = p[j - 1] && s[i - 1] == p[j - 1] || ...。此时在写一个f(i - 1, j)的方程，你会发现, 后面的部分都是一一对应的，整合这两个方程得到：f(i, j) = f（i, j -2) || f（i - 1, j）&& s[i] == p[j]
4. 初始状态 f(0,0)=true；循环枚举 i 从 0 到 n；j 从 1 到 m。因为 f(0,j)有可能是有意义的，需要被转移更新。
5. 最终答案为 f(n,m)。

💚 代码实现

class Solution {
public:
    bool isMatch(string s, string p) {
        // 动态规划

        int n = s.size(), m = p.size();
        s = ' ' + s, p = ' ' + p;   // 从字符串1开始

        vector<vector<bool>> f(n + 1, vector<bool>(m + 1, false));
        f[0][0] = true;
        for(int i =0; i <=n; i ++)
            for(int j = 1; j <= m; j ++)
            {
                //if(j + 1 <= m && p[j + 1]== '*') continue;
                if(i && p[j] != '*')
                    f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
                else if (p[j] == '*')
                    f[i][j] = f[i][j - 2] || i && f[i - 1][j] && (s[i] == p[j - 1] || p[j -1] == '.');
            }

        return f[n][m];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

执行结果：

💙 时间复杂度分析

状态数为 O(nm)，每次转移仅需常数时间，故总时间复杂度为 O(nm)。

如果觉得对你有帮助的话:
👍 点赞，你的认可是我创作的动力！
🧡 收藏，你的青睐是我努力的方向！
✏️ 评论，你的意见是我进步的财富！