目录

一、支持向量机

二、拉格朗日对偶

三、SMO算法（序列最小优化算法） 

四、线性不可分核函数

---

一、支持向量机

        如图所示为蓝红两类样本，SVM的工作就是找到一个超平面，可以使得这两类样本更好的分开，图中所示的红线就是SVM所求得的超平面，图中的虚线与超平面平行，d表示两类样本到超平面的距离，我们的目的就是最小化W。

        原理：margin为红线左右平移得出的 2 条虚线，要使红线为最优分割线，就要使margin最大化，从而使得两类更好的分割开。

        公式：设两条虚线分别为，则两条虚线之间的距离为。

如图2d即为margin，要使得2d最大，则使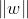最小。该公式是控制两个样本之间的距离，那应该如何限制两类样本的取值范围呢？如下图所示，蓝色样本的y（类别标签）为-1，红色样本的y（类别标签）为1，对两个虚线方程进行一定的变换（如下图所示），则得到。

 举个例子：

        下图中中有是哪个样本，其中x1，x2是属于第一类，y=1，x3属于第二类，y=-1。根据约束求出最优超平面。

（1）我们首先使得两条虚线之间的距离最大化，故根据上述的公式得出要最小化，从而得到。

（2）我们定义约束为，将三个点带入该式中得到三个约束条件。

我们参考之前一道例题对该提进行求解，应用的思想是使用拉格朗日求不等式约束的极值。

具体参考链接：数学基础（五）最优化理论（最优化，无约束，有约束，拉格朗日乘子的意义，KKT条件）

 首先求解f(x)，g1，g2，g3的梯度，下图中是以列向量的形式表示。

再带入公式

再将g1，g2，g3带入公式

约束

如下图所示：

 求解结果如图所示，λ=0 处的约束是不起作用的（KKT条件）。

二、拉格朗日对偶

拉格朗日对偶是解决SVM问题的一个很好的工具。

下面例子中，最优化目标为：

约束条件为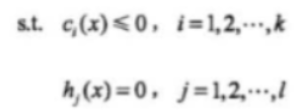：，该约束条件既有等式也有不等式。

我们引入广义拉格朗日函数：

我们在不等式前面乘α，等式前面乘β，α和β表示拉格朗日乘子，其中。

在x固定的情况下，我们可以求出α，β使得L最大：

假设某个x不满足约束条件，

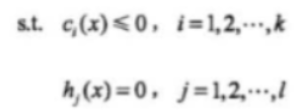则

不满足约束时最大值的求解：

满足约束时最大值的求解：，，，则当α=0时取得最大值。

完整过程如下所示： 

因此，原始问题满足： 

回到问题本身，要求最小值：

        上述问题的最小值求解中，是先求最大值再求最小值，这个过程不是很好求，那我们转换一下思路，先求最小值，再求最大值。

三、SMO算法（序列最小优化算法） 

下面我们来看SVM的优化问题： 

我们将SVM的最优化问题转换成拉格朗日求极值的方法：

就转换成

 构建广义拉格朗日函数：

 其中，。

 对L求解w和b的梯度，求得L取最小值时的条件。

将求得的条件代入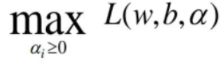中得到：

​​​​​

这样SVM问题就转化为拉格朗日等式约束问题：

下式中优化的目标是 α，优化的约束是一个等式和KKT条件。

 上述结果即：

四、线性不可分核函数

        上述我们所讲的题目都是可以直接用一条直线区分开，但是还有一些分类问题无法用直线区分开，如下图中的左图，圆内是一类，圆外是一类。那针对这种分布的样本，我们又应该如何求解呢？

针对这种问题我们就需要做空间的变换：

我们将椭圆方程变换为直线方程。