2022宁夏杯D 包装纸箱设计

题目

某企业为其下游某公司生产包装纸箱，生产所需原材料为三层瓦楞纸和五层瓦楞纸两种，其规格尺寸和成本如表 1 所示

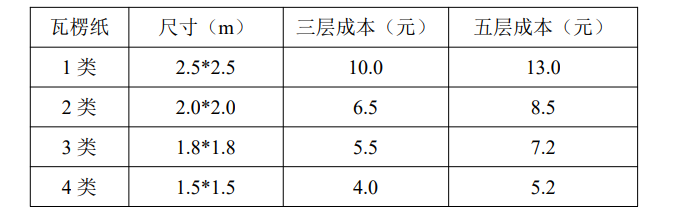
下游公司的日订单数见表 2，且合同要求所有纸箱均为一页成型箱，也即瓦楞纸箱在制造过程中只允许单拼，瓦楞纸边角料可以以每平米 0.3 元在其企业内部回收利用。请建模解决以下问题：

思路

第一问

问题：利用表 2 中的数据，确定该企业 1 天的生产计划，使其利润最大。

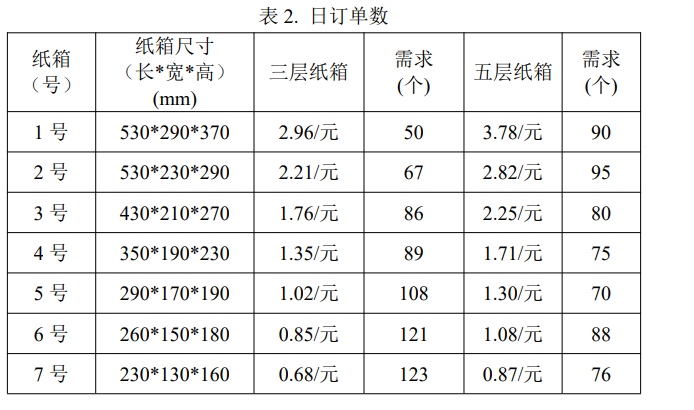
很显然，这就是一个线性规划问题，自己设置好约束函数和目标函数。说白了，你就把它当作数学问题来做，这里的变量本来就不多，大学生学过数学的人应该都会。

建立好模型后，求解即可，有以下两种方案完成：

1. Matlab求解线性规划，这个我去年就讲过了：线性规划模型详解
2. lingo求解线性规划我讲过了，不重复说：Lingo解决线性，非线性，助力国赛！

第二问

问题：如果实际中提供给下游公司的纸箱在容积误差 20%之内可以以大纸箱代替小纸箱供货，那么新的最优生产计划是什么？

这肯定就是个最优化问题了，很显然用到启发式算法，最常见的就是遗传算法咯。做出数学模型后带入算法即可得到最优结果，关于启发式算法我最近更新了七八个，自己到我数模专栏看。数学模型建立就是基于第一问的模型改一下就好了。

第三问

问题：哪一种纸箱的需求变化对生产计划最为敏感

这个问题就是敏感性分析。这是很重要的方法，美赛年年都有。对x1和x2两个纸箱分别做敏感性分析，看谁更敏感就好了。

这里我也讲过了：用Python敏感性分析,如此轻松简单

值得参考的文献

看一看不后悔：

https://zly201.github.io/2020/09/01/%E5%9F%BA%E4%BA%8E%E9%81%97%E4%BC%A0%E7%AE%97%E6%B3%95%E5%92%8C%E7%BA%BF%E6%80%A7%E8%A7%84%E5%88%92%E7%9A%84%E5%BF%AB%E9%80%92%E5%8C%85%E8%A3%85%E7%9B%92%E4%B8%8B%E6%96%99%E9%97%AE%E9%A2%98%E7%A0%94%E7%A9%B6/