“有一些树状数组高级操作，能干很多事情，但可能也比较复杂，线段树常数大但是完全包含树状数组，所以很多问题能用树状数组解决的同样也可以用线段树解决。”

知识点

---

一 . 定义

树状数组，也称二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树，其最初是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和。

原理：（待填坑）

---

模板题

1 . 基础版：洛谷 P3374 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 x

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 n,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 ii 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 x 个数加上 k

• 2 x y 含义：输出区间 [x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出 #1

14
16

说明/提示

【数据范围】

对于 30% 的数据，，；
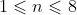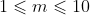对于 70% 的数据，；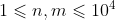
对于 100% 的数据，。

样例说明：

故输出结果14、16

#include 
#include 
#include 
#include 
using namespace std;
const int maxn=1e8+5;
int a[maxn];
int n,m;
int lowbit(int x) //x的二进制表达式最右边的1的值
{
	return x & -x; //计算机的补码表示，-x表示x按位取反
}
 
void add(int x,int y)  //区间修改；
{
	while(x<=n)
	{
		a[x]+=y;
		x+=lowbit(x);
	}
}
 
int sum(int x)
{
	int result=0;
	while (x>0)
	{
		result+=a[x];
		x-=lowbit(x);
	}
	return result;
}
 
int main()
{
	
	cin>>n>>m;
	for(int i=1;i<=n;++i)
	{
		int p;
		cin>>p;
		add(i,p);
	}
	
	for(int i=1;i<=m;++i)
	{
		int num,x,y;
		cin>>num>>x>>y;
		if(num==1)
		{
		add(x,y);
		}
		if(num==2)
		{
		cout<<sum(y)-sum(x-1)<
		}
	}
	return 0;	
}

---

 2 . 增强版：洛谷 P3368 【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 x；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含 N 个用空格分隔的整数，其中第 ii 个数字表示数列第 i 项的初始值。

接下来 M 行每行包含 2 或 4个整数，表示一个操作，具体如下：

操作 1： 格式：1 x y k 含义：将区间 [x,y] 内每个数加上 k；

操作 2： 格式：2 x 含义：输出第 x 个数的值。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出 #1

6
10

说明/提示

样例 1 解释：

故输出结果为 6、10。

数据规模与约定

对于 30% 的数据：，；

对于 70% 的数据：，；

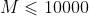对于 100% 的数据：，，保证任意时刻序列中任意元素的绝对值都不大于 。

---

 1 . 使用暴力

#include 
#include 
#include 
#include 
using namespace std;
const int maxn=1e8+5;
int a[maxn];
 
int main()
{
	int n,m;
	cin>>n>>m; //n,m的数据范围可达到
	for(int i=1;i<=n;++i)
	{
		cin>>a[i];
	}
	
	for(int i=1;i<=m;++i) 
	{
		int num,x,y,k;
		cin>>num;
		if(num==1)
		{
			cin>>x>>y>>k;
		for(int j=x;j<=y;++j)	//若区间数x,y特别大，所需时间长
			{
			a[j]+=k;
			}
		}
		else if(num==2)
		{
			cin>>x;
			cout<
		}
	}
	return 0;
}

 2 . 使用树状数组+差分优化

#include 
#include 
#include 
#include 
using namespace std;
const int maxn=1e8+5;
int a[maxn],b[maxn];
int n,m;
int lowbit(int x)
{
	return x & -x;
}
 
void add(int x,int y)
{
	while(x<=n)
	{
		b[x]+=y;
		x+=lowbit(x);
	}
}
 
int sum(int x)
{
	int result=0;
	while(x>0)
	{
		result+=b[x];
		x-=lowbit(x);
	}
	return result;
}
 
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;++i)
	{
		cin>>a[i];
		add(i,a[i]-a[i-1]); 
	//a[i]-a[i-1]求得差分数组；
	}
	
	for(int j=1;j<=m;++j)
	{
		int num;
		cin>>num;
		if(num==1)
		{
		int x,y,k;
		cin>>x>>y>>k;
		add(x,k);  //等价于b[x]+=z;即从x以后的数都加上k
		add(y+1,-k);	//b[y+1]-=z;即从y+1后恢复原来的数
               		 //这两个式子是差分的精髓
		}
		else if(num==2)
		{
			int x;
			cin>>x;
			cout<<sum(x)<
		}
	}
	return 0;
}