【机械】基于Matlab求解Hoek-Brown应变软化岩体GRC曲线

1 内容介绍

基于岩体的强度参数随着最大塑性主应变的增加而逐渐演化这一力学行为,采用广义Hoek-Brown(H-B)强度准则,以最大塑性主应变作为应变软化参数,假设广义Hoek-Brown强度准则中的强度参数m,s和a为最大塑性主应变的双线性函数条件下,通过理论推导给出岩体应变软化曲线非线性表达式的求法。最后结合算例分析度参数m,s和a的演化规律对岩体应变软化行为的影响。研究结果表明:强度参数m和s的残余值越大且a的残余值越小,则软化曲线下降得越缓和,岩体的残余强度越大。​

2 仿真代码

%%%%%%%%%%%%%%%%%%%无支护时弹塑性应变软化计算程序,压为正

clear;

clc;

close;

tic;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

b=3; %隧道半径

s0=15e6; %初始地应力

E=5.7e9; %初始变形模量

v=0.25; %泊松比

G0=E/(1+v)/2; %剪切模量

Mp=2.0;  %胡克布朗参数

Mr=0.6;  %

Sp=4e-3;   %

Sr=2e-3;   %

Ap=0.51;

Ar=0.6;

scp=30e6;

scr=20e6;

Dp=15;   %峰值剪涨角

Dr=5;   %残余剪涨角

gamastarp=0.01; %临界塑性剪应变

n=200; %塑性区划分的环数

Pic = fsolve(@HBfun,0)  %临界支护压力

xh=500; %卸荷500次

for j=1:xh

Pi(j,1)=Pic*(1-j/xh); %支护应力

sr=zeros(n+1,1); esr=zeros(n+1,1); st=zeros(n+1,1); deta_sr=zeros(n+1,1); deta_st=zeros(n+1,1);

er=zeros(n+1,1); erp=zeros(n+1,1); ere=zeros(n+1,1); deta_erp=zeros(n+1,1); deta_ere=zeros(n+1,1);

et=zeros(n+1,1); etp=zeros(n+1,1); ete=zeros(n+1,1); deta_etp=zeros(n+1,1); deta_ete=zeros(n+1,1);

H=zeros(n+1,1); He=zeros(n+1,1); gamap=zeros(n+1,1); M=zeros(n+1,1); A=zeros(n+1,1); sc=zeros(n+1,1);% G=zeros(n+1,1);

S=zeros(n+1,1); D=zeros(n+1,1); rou=zeros(n+1,1); deta_rou=zeros(n+1,1); roue=zeros(n+1,1); U=zeros(n+1,1); 

sb=0;

       end

       Rp(j,1)=b/rou(n+1,1); %每一次的塑性区半径

       RR(:,j)=b/rou(n+1,1)*rou; %每一次卸荷塑性区的围岩环半径

       if sb>0

          Rs(j,1)=b/rou(n+1,1)*rou(n+1-sb,1);   %每一次的残余区半径

       else

          Rs(j,1)=0;

       end

       u(:,j)=U*Rp(j,1)*1000;  %u每一列表示每一次支护压力下塑性区的位移

   end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%弹性区计算

%else      

end

toc

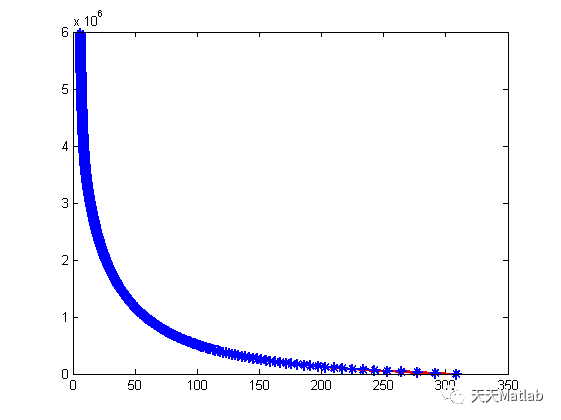
plot(u(n+1,:),Pi,'r-*','MarkerSize',8,'LineWidth',2,'MarkerEdgeColor','b')

%plot(u(n+1,:),Pi,'r-o','MarkerSize',4,'LineWidth',2,'MarkerEdgeColor','b','MarkerFaceColor','w')

3 运行结果

4 参考文献

[1]孙闯, 张涛, 顾杨明. 基于Hoek-Brown应变软化模型的深部巷道锚杆受力特征研究[J]. 防灾减灾工程学报, 2016(3):6.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。