高比例风电电力系统储能运行及配置分析

目录

摘  要

0 目标函数和约束条件

1 第一题

2 第二题

3 第三题

4 第四题

6 第六题

7 第七题

8 所有题代码及文章详细讲解

9 结论：

10 参考文献

---

摘  要

高比例风电电力系统储能运行及配置分析

摘  要

要实现碳中和，就需要找到清洁能源代替非清洁能源这一切实可行的方法；另一方面，能源需求和经济发展之间具有同步增长规律。也就是说，当中国经济维持上升趋势时，能源需求量也会相应增加，若不对单位GDP相应能源的碳排放量进行有效约束，碳中和目标就很难实现。

风能是可再生清洁能源，因总资源蕴藏量巨大，可再生，无污染，日益引起世界各国关注。伴随着风电在电源结构中所占比重的日益提高，风电自身存在的随机性，波动性和不稳定性等问题对于电力系统的安全和稳定运行产生了日益显着的影响。大规模风电消纳问题始终是个棘手问题。

储能技术对于解决风电消纳比例较高，提高系统可靠性具有重要意义。充分利用风能资源可以实现绿色发展和节能降耗，但风力发电特点不同于常规发电，风电具有间歇性和波动性，大范围风能并网对电网造成影响。为了解决高渗透分布式风电并网给配电网带来的安全性和可靠性等问题，储能技术成为保证风电消纳和提高系统经济效益的有效手段。研究电力系统储能系统的功能定位和配置原则，有着十分重要的意义。

关键词：风电消纳；储能容量配置；成本最优

0 目标函数和约束条件

目标函数为系统发电总成本最小，发电总成本=火电成本+风电成本+储能成本+弃风损失+失负荷损失；

火电成本=运行维护成本+发电煤耗成本+碳捕集成本，

当使用传统的火电机组煤耗量计算公式对该最优化调度问题进行建模时，将会得到一个二次规划问题，这是由于火电机组的煤耗量是关于机组出力的一元二次函数，使得该问题的目标函数中含有非线性的部分，而当模型中火电机组的个数或调度周期增加时，求解该最优化问题的时间成本和难度将大大上升。基于此，为了降低模型求解难度，加快最优化求解计算速度，本文使用分段线性化方法将火电机组的二次煤耗量计算公式转为一次函数，进而使整个最优化模型转化为线性规划模型。火电机组的煤耗量函数图像如下，其中实线表示分段线性化处理后的火电机组煤耗量函数，虚线表示分段线性化处理之前的火电机组煤耗量函数。

                       

                               图1 火电机组煤耗量函数曲线对比

分段线性化后的火电机组煤耗量函数表达式为：

                           FL(t)=FMin+∑i=1NaiPi(t)" role="presentation" style="position: relative;">FL(t)=FMin+∑Ni=1aiPi(t)$F^L(t)=F_{\mathrm{Min}}+\sum _{i=1}^N{a}_i{P}_i(t)$            （1）

其中：

                            ai=Fi+1−FiPi+1−Pi" role="presentation" style="position: relative;">ai=Fi+1−FiPi+1−Pi$a_i=\frac{F_{i+1}-F_i}{P_{i+1}-P_i}$                                 （2）

                        0≤Pi(t)≤Pi+1−PiN" role="presentation" style="position: relative;">0≤Pi(t)≤Pi+1−PiN$0\le P_i(t)\le \frac{P_{i+1}-P_i}{N}$                         （3）

式中：ai" role="presentation" style="position: relative;">ai$a_i$是第i" role="presentation" style="position: relative;">i$i$段的斜率；Fi" role="presentation" style="position: relative;">Fi$F_i$是第段的最大煤耗量；N" role="presentation" style="position: relative;">N$N$是分段数。

风电成本=运维成本=发电量×单位电量运维成本；

储能成本=投资成本+运维成本；

储能的成本函数为：

                    C=c1PES+c2EES" role="presentation" style="position: relative;">C=c1PES+c2EES$C=c_1{P}_{ES}+c_2{E}_{ES}$                （4）

式中，PES" role="presentation" style="position: relative;">PES$P_{ES}$为储能配置功率；EES" role="presentation" style="position: relative;">EES$E_{ES}$为系统中储能配置容量；c1" role="presentation" style="position: relative;">c1$c_1$为单位功率费用（元/kW），对于锂电池、铅酸等电池储能，主要为功率变流器（PCS）的单位购置费用；c2" role="presentation" style="position: relative;">c2$c_2$为单位容量费用（元/(kW·h)），主要为电池的单位容量购置费用。

其中PES和EES得满足以下约束条件

               {pES(i)≤PES≤PM1SOCM−SOC0∑k=1iα(i)pES(i)Δt≤EES≤EM" role="presentation" style="position: relative;">{pES(i)≤PES≤PM1SOCM−SOC0∑ik=1α(i)pES(i)Δt≤EES≤EM$\{\begin{array}{l}{p}_{ES}(i)\le P_{ES}\le P_M\\ \frac{1}{SO{C}_M-SO{C}_0}\sum _{k=1}^i\alpha (i)p_{ES}(i)\mathrm{\Delta }t\le E_{ES}\le E_M\end{array}$（5）

式中，i" role="presentation" style="position: relative;">i$i$为计算时段（=1,2,∙∙∙,96）；PES" role="presentation" style="position: relative;">PES$P_{ES}$、EES" role="presentation" style="position: relative;">EES$E_{ES}$分别为储能最大功率和容量；SOCM" role="presentation" style="position: relative;">SOCM$SO{C}_M$为电池储能系统允许的最高荷电状态，SOC0" role="presentation" style="position: relative;">SOC0$SO{C}_0$为电池储能系统每日的初始荷电状态。将储能的充放电功率定义为充电时PES(i)>0" role="presentation" style="position: relative;">PES(i)>0$P_{ES}(i)>0$、放电时PES(i)≤0" role="presentation" style="position: relative;">PES(i)≤0$P_{ES}(i)\le 0$，考虑储能充放电效率ηc" role="presentation" style="position: relative;">ηc${\eta }_c$为90%，且在运行过程中保持不变，令

                        α(i)={ηc1ηd" role="presentation" style="position: relative;">α(i)={ηc1ηd$\alpha (i)=\{\begin{array}{l}{\eta }_c\\ \frac{1}{{\eta }_d}\end{array}$（6）

 约束条件考虑系统功率平衡,

                                 {180≤P1(t)≤60090≤P2(t)≤30045≤P3(t)≤1500≤Pwind (t)≤Pwind-IC P1(t)+P2(t)+P3(t)+Pwind (t)+Pse =Load⁡(t)" role="presentation" style="position: relative;">⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪180≤P1(t)≤60090≤P2(t)≤30045≤P3(t)≤1500≤Pwind (t)≤Pwind-IC P1(t)+P2(t)+P3(t)+Pwind (t)+Pse =Load(t)$\{\begin{array}{l}180\le P_1(t)\le 600\\ 90\le P_2(t)\le 300\\ 45\le P_3(t)\le 150\\ 0\le P_{\text{wind }}(t)\le P_{\text{wind-IC }}\\ P_1(t)+P_2(t)+P_3(t)+P_{\text{wind }}(t)+P_{\text{se }}=\mathrm{Load}(t)\end{array}$     （7）

P1(t)" role="presentation" style="position: relative;">P1(t)$P_1(t)$其中为机组1在t" role="presentation" style="position: relative;">t$t$时段的功率，P2(t)" role="presentation" style="position: relative;">P2(t)$P_2(t)$为机组2在t" role="presentation" style="position: relative;">t$t$时段的功率，P3(t)" role="presentation" style="position: relative;">P3(t)$P_3(t)$为机组3在t" role="presentation" style="position: relative;">t$t$时段的功率，Pwind(t)" role="presentation" style="position: relative;">Pwind(t)$P_{wind}(t)$为风电在时段的功率，Pwind−IC" role="presentation" style="position: relative;">Pwind−IC$P_{wind-IC}$为风电的装机容量，Load(t)" role="presentation" style="position: relative;">Load(t)$Load(t)$为系统在t" role="presentation" style="position: relative;">t$t$时段的负荷功率。

储能相关约束为：

(1)充放电约束： state ={1, if :Pse≥00, if :Pse≤0" role="presentation" style="position: relative;"> state ={1, if :Pse≥00, if :Pse≤0$\text{ state }=\{\begin{array}{l}1,\text{ if }:P_{se}\ge 0\\ 0,\text{ if }:P_{se}\le 0\end{array}$（8）

式中，Pse" role="presentation" style="position: relative;">Pse$P_{se}$ 为蓄电池出力，state" role="presentation" style="position: relative;">state$state$为蓄电池充/放电标志。

(2)蓄电池最大出力：

−0.35×Pse−IC≤−∑t=196(Pdis(t)0.95+0.95×Pcha(t))≤0.55×Pse−IC" role="presentation" style="position: relative;">−0.35×Pse−IC≤−∑96t=1(Pdis(t)0.95+0.95×Pcha(t))≤0.55×Pse−IC$-0.35\times P_{se-IC}\le -\sum _{t=1}^{96}\left(\frac{P_{dis}(t)}{0.95}+0.95\times P_{cha}(\mathrm{t})\right)\le 0.55\times P_{se-IC}$  （9）

式中，Pse−Ic" role="presentation" style="position: relative;">Pse−Ic$P_{se-Ic}$为储能容量，Pdis" role="presentation" style="position: relative;">Pdis$P_{dis}$为蓄电池在t" role="presentation" style="position: relative;">t$t$时刻放电功率，Pcha(t)" role="presentation" style="position: relative;">Pcha(t)$P_{cha}(t)$为蓄电池在t" role="presentation" style="position: relative;">t$t$时刻充电功率。 

基于Matlab2018b平台，使用Yalmip对该最优化调度模型进行建模，并调用Cplex商业求解器进行求解，得到系统最优运行计划。我们还使用粒子群算法作为对比方法。但是在第一问中，发现粒子群的功率分配以及最后的成本效果不如Cplex商业求解器，第一题中包含Python编程的粒子群算法求解该问题。我们在第一问画图做说明。在之后的几题，我们就只使用Cplex商业求解器来对问题进行求解。

1 第一题

1.1.以最小发电成本为目标函数，按照日负荷曲线，考虑每台机组的发电成本，将负荷分配给三台火电机组，并计算系统单位供电成本。

此时仅有火电，系统发电总成本=火电成本+失负荷损失。单位碳捕集成本改变时，机组功率变化变化在5MW以内，从机组日发电计划图中很难看出差别。所以我们以单位碳捕集成本分别为0元/t时为例，机组日发电计划曲线如下图所示，

图1.1

针对单位碳捕集成本为100元/t时，各台机组发电功率变化情况绘制如图1.2，当碳捕集单位成本变化的时候，从第21个时段开始，各机组的出力出现变化如下图所示。

图1.2

由于机组A的碳排放量最低，机组C的碳排放量最高，优先增加机组A的发电功率，减少机组C的发电功率，其次再降低机组B的发电功率。

在碳捕集单位成本为100元/吨的情况下，碳捕集成本占火电成本的41.097%。面对高额的碳捕集成本，应该充分利用风能资源，这样不仅能有效降低供电成本，而且从远期来看，要实现国家提出的“双碳”目标，新能源大规模发展是必然要求，尽可能达到绿色发展、节能降耗，电力系统低碳转型的关键在于高比例新能源的消纳利用。

单位碳捕集成本分别为0元/t、60元/t、80元/t、100元/t时，系统单位供电成本见表2。

表2 风电电量占比为0时系统相关指标统计

表3 风电电量占比为0时系统相关指标统计（粒子群方法）

需要第一题程序点这里：🍞正在为您运送作品详情

2 第二题

先考虑风电装机300MW直接替代机组3的发电功率曲线，观察系统功率平衡发生的变化情况。然后在此场景下，以最小发电成本为目标函数，将负荷分配给两台火电机组1、2和风电机组，绘制机组日发电计划图。再将风电装机容量作为一个决策变量，以最小发电成本为目标函数，求取最小发电成本对应的风电装机容量，绘制机组日发电计划图。

2.1. 风电装机300MW、直接替代机组3时，机组日发电计划曲线如图2.1（1）所示

图2.1（1）

系统功率平衡发生变化如下，

图2.1（2）

功率为正的部分为弃风的功率时段，功率为负的部分为失负荷的时段。有47个时段存在弃风的情况，弃风电量达到698.404MWh；有49个时段存在失负荷的情况，失负荷电量达到279.799MWh。

2.2. 此时的系统发电成本=火电成本+风电成本+弃风损失+失负荷损失，以最小成本为目标函数，绘制此时的机组日发电计划曲线，如下图所示

有5个时段存在弃风的情况，弃风电量达到19.988MWh；不存在失负荷的情况。

2.3. 在此场景下，为减少弃风，则需要又不失负荷。再以最小成本为目标函数，此时求得的风电装机容量仍然为300MW，即不考虑降低风电的接入装机容量。风电的运维成本低，这也是我们提倡不断推进风电并网促进消纳风电的原因。此时的机组日发电计划曲线没有改变，还是图2.2(1)。

如果需要第二题代码，点这里：🍞正在为您运送作品详情

3 第三题

先考虑风电装机600MW直接替代机组2的发电功率曲线，观察系统功率平衡发生的变化情况。然后在此场景下，以最小发电成本为目标函数，将负荷分配给火电机组1、3和风电机组，绘制机组日发电计划图。再将风电装机容量作为一个决策变量，以最小发电成本为目标函数，求取最小发电成本对应的风电装机容量，绘制机组日发电计划图。

3.1.风电装机600MW、直接替代机组2时，机组日发电计划曲线如下图所示

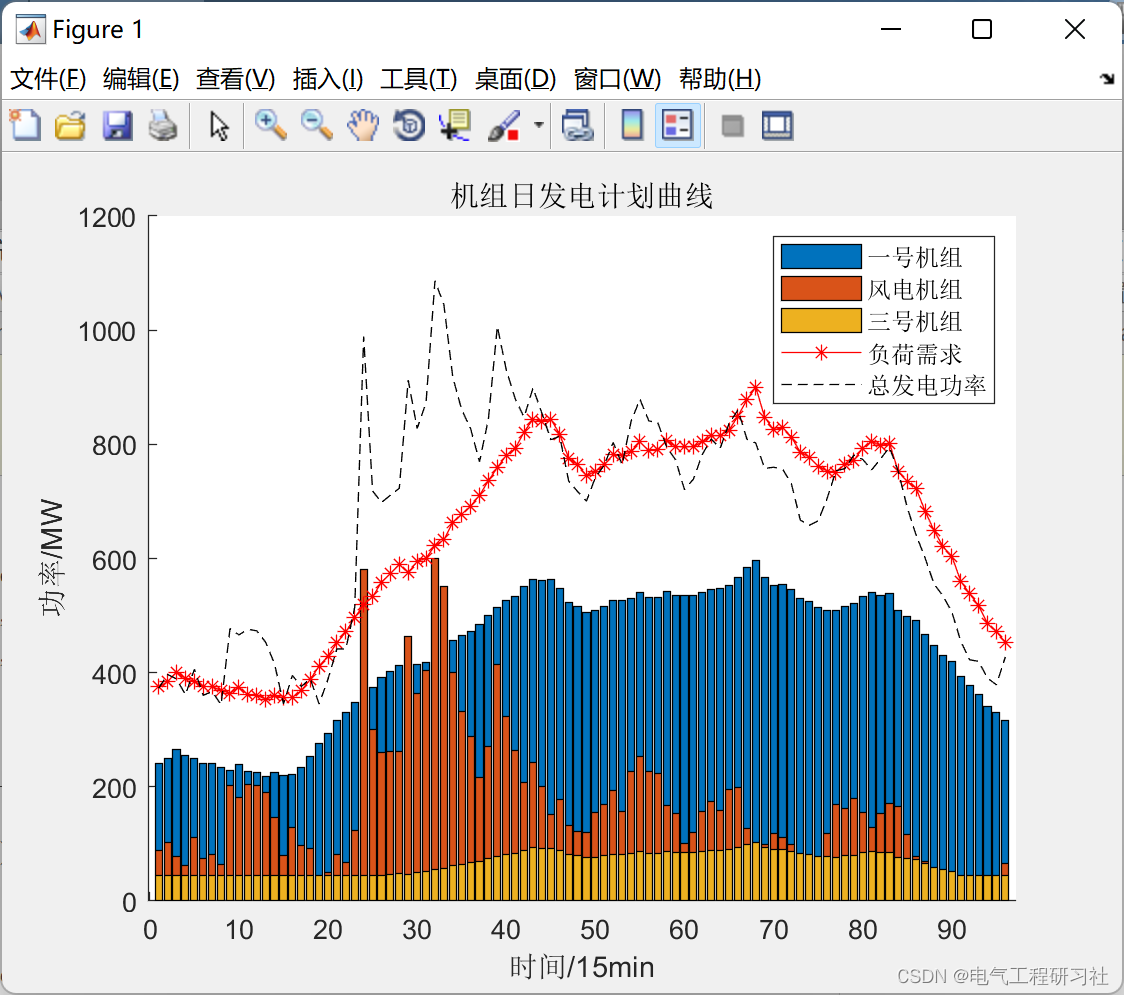
图3.1（1）

系统功率平衡发生变化如下，

图3.1（2）

有83个时段存在弃风的情况，弃风电量达到2520.041MWh，有13个时段存在失负荷的情况，失负荷电量达到75.934MWh。

3.2. 此时的系统发电成本=火电成本+风电成本+弃风损失+失负荷损失，再以最小成本为目标函数，此时的机组日发电计划曲线如下图所示

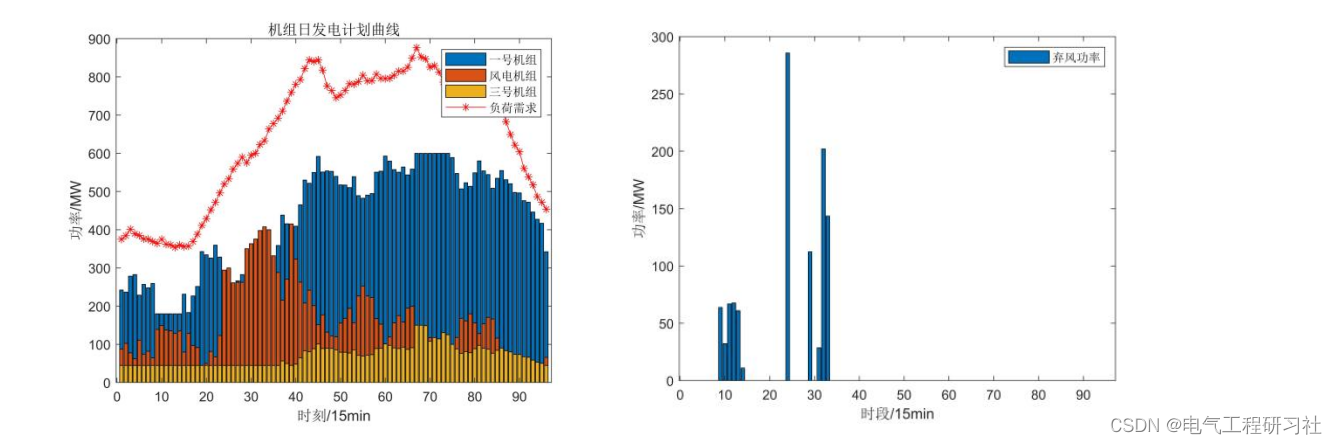
                  图3.2（1）                                                图3.2（2）

有11个时段存在弃风的情况，弃风电量达到268.586MWh，有2个时段存在失负荷的情况，失负荷电量达到12.254MWh。

3.3. 在此场景下，为不失负荷。再以最小成本为目标函数，求最优风电接入容量。

针对4种碳捕集单位成本，分别求得的风电装机容量见下表，

表4

即当单位碳捕集成本为 0元/t、60元/t、80元/t、100元/t时，在此场景下，为不失负荷，风电接入容量分别可增加多少372.187MW、494.871MW、532.677MW、573.996MW。

分别拿单位碳捕集成本为 0元/t、100 元/t时举例说明，绘制其对应的机组日发电计划曲线如下图所示。

              图3.3（1） 0元/t                     图3.3（2） 0元/t   

有23个时段存在弃风的情况，弃风电量为1139.160MWh，存在大量的弃风现象。

           图3.3（3）100 元/t                 图3.3（4）100 元/t

有30个时段存在弃风的情况，弃风电量为1773.647MWh，存在大量的弃风现象。

当系统负荷处于较小值时，风电功率输出可能达到最大，火电则要调整出力，让出负荷由风电供电。但受常规火电微增特性的制约，有最小出力运行条件。如果能在电网负荷低谷时段适度弃风，不仅能够减少常规火电降出力运行的压力，也能够提高电网接纳风电并网能力，从而提高整个电力系统运行的安全性和经济性[1]。

第三题需要代码点这里：🍞正在为您运送作品详情

4 第四题：含高比例风电电力系统最小供电成本模型

针对4种碳捕集单位成本，系统单位供电成本见表 5和表6。

表 5 风电装机 300MW 替代机组 3 时系统相关指标统计

表 6 风电装机 600MW 替代机组 3 时系统相关指标统计

针对上述 2-3 风电替代场景，之所以在这4种碳捕集单位成本下，弃风电量没有发生变化，是因为在每一个弃风时段，火电机组都已经达到最小技术出力，火电机组容量无法再降低，所以必须选择弃风。即仍然存在着弃风情况，根据观研报告网关于2017-2021年中国弃风量及弃风率年度变化统计情况，2021年下半年，全国弃风量约126.4亿千瓦时,弃风率3.6%，因此仍然需要借助储能等对负荷分布具有调控能力的技术来提高风电的消纳水平[2]。

运行图像：

 

第四题代码需要点这里：🍞正在为您运送作品详情

5 第五题：含储能的高比例风电电力系统最小供电成本模型

先考虑风电装机900MW直接替代机组2、3的发电功率曲线，观察系统功率平衡发生的变化情况。然后在此场景下，以最小发电成本为目标函数，将负荷分配给火电机组1和风电机组，绘制机组日发电计划图。再将储能容量作为一个决策变量，发电成本考虑储能成本，以最小发电成本为目标函数，求取最小发电成本对应的储能配置容量，绘制机组日发电计划图。

5.1.风电装机900MW、直接替代机组 2、3 时，机组日发电计划曲线如下图所示

图5.1（1）

系统功率平衡发生变化如下，

图5.1（2）

 

有44个时段存在弃风的情况，弃风电量达到1966.941MWh，有52个时段存在失负荷的情况，失负荷电量达到941.086MWh。

5.2.此时的系统发电成本=火电成本+风电成本+弃风损失+失负荷损失，再以最小成本为目标函数，此时的机组日发电计划曲线如下图所示

图5.2.（1）

系统功率平衡发生变化如下，

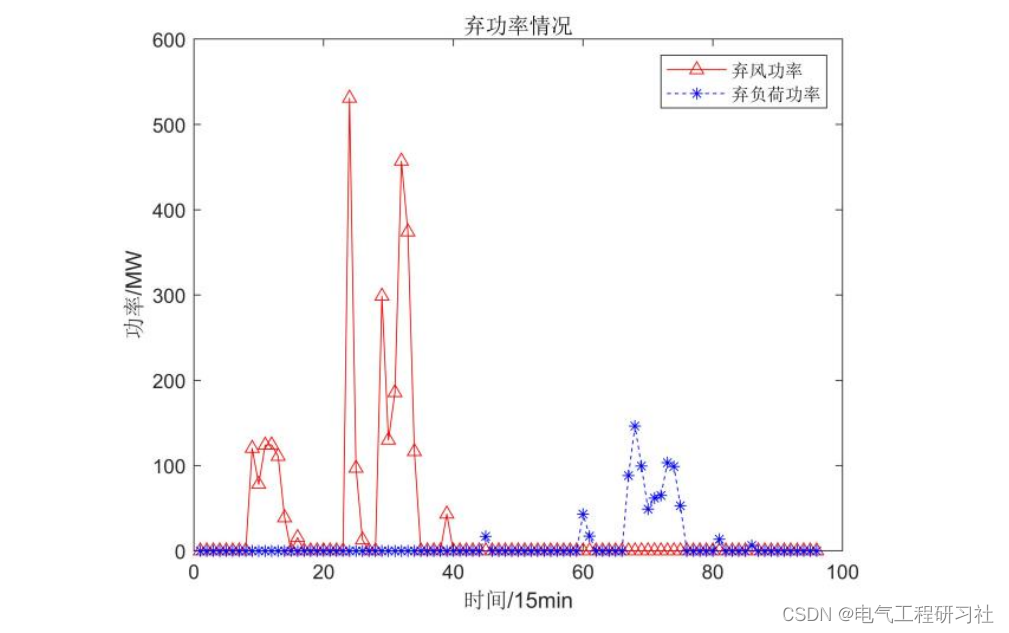
图5.2.（2）

有19个时段存在弃风的情况，弃风电量达到714.274MWh，有14个时段存在失负荷的情况，失负荷电量达到215.541MWh。

单位碳捕捉成本（取60元/t），此时系统单位供电成本见表7

表7 风电装机900MW替代机组2、3时系统相关指标统计

5.3.规模化风电并网后，火电机组按照常规出力范围和调峰要求参与系统运行调度时，系统常无法平 衡规模化风电的大幅出力变化，从而造成大量弃风， 限制了风电的消纳。为了充分有效利用风电等可再生能源，需要配置储能系统[3]。考虑采用储能设备对负荷曲线进行削峰填谷，从而将负荷高峰期电网的部分负备用容量转移到低谷期，即可解决出现的调峰瓶颈以及由此造成的弃风问题。

此时的系统发电成本=火电成本+风电成本+储能成本+弃风损失+失负荷损失。以系统发电总成本最小为优化目标，约束条件考虑系统功率平衡约束。

在容量配置方面综合考虑储能所带来的节煤收益、弃风损失和失负荷损失，以系统系统发电成本最小为目标函数对储能容量优化配置进行建模，通过利用Cplex商业求解器对模型求解，得到储能最优容量。求得在满足不失负荷条件下需要配置的最小储能容量为944.420MW。

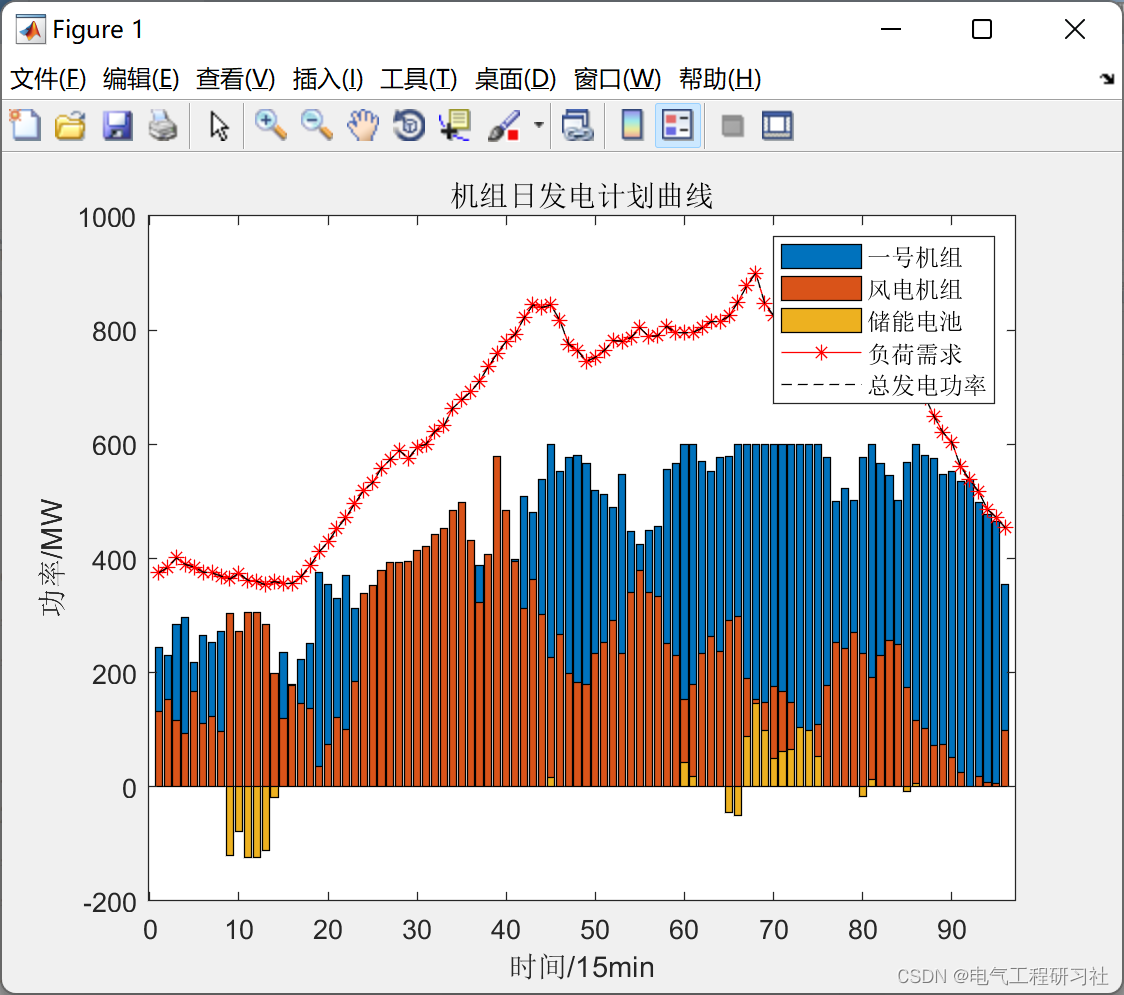
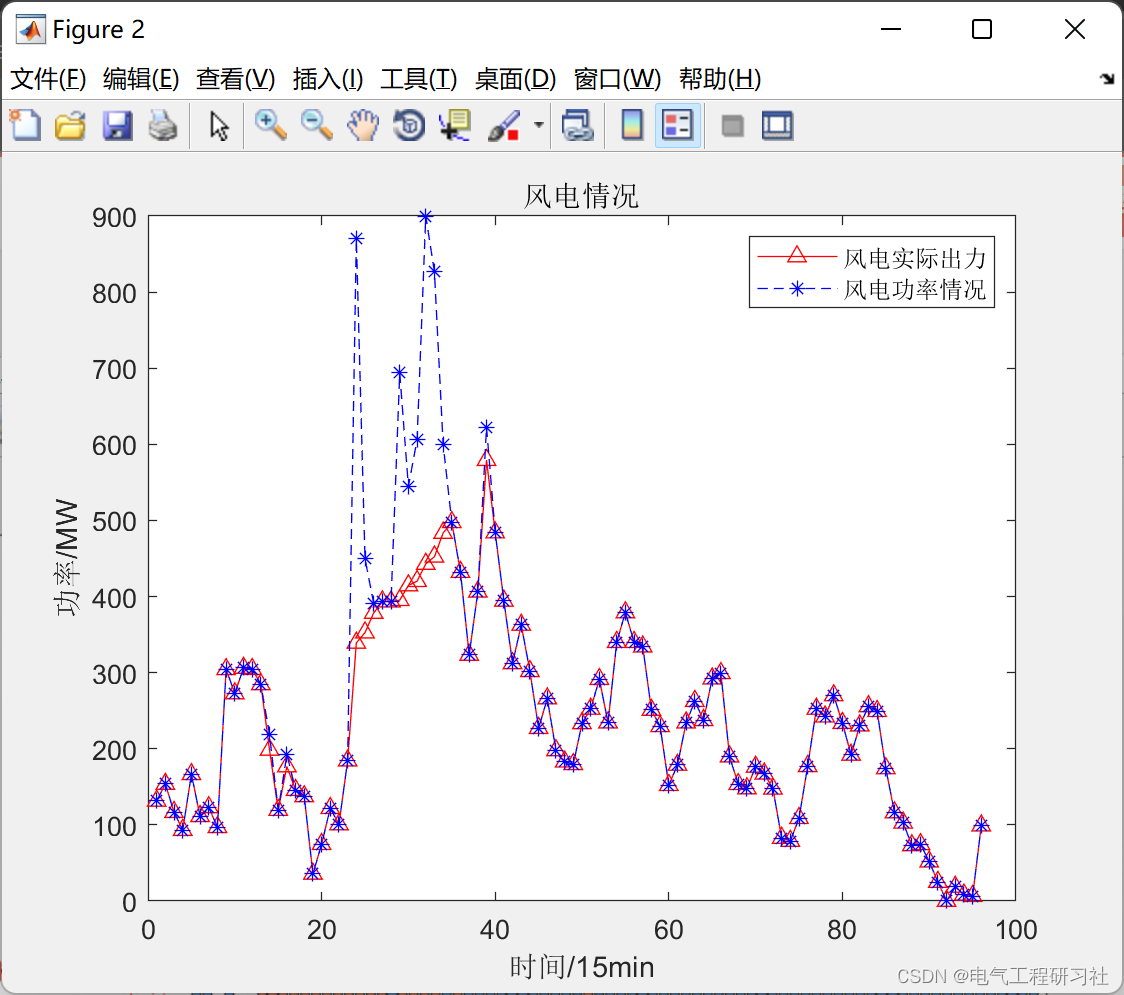
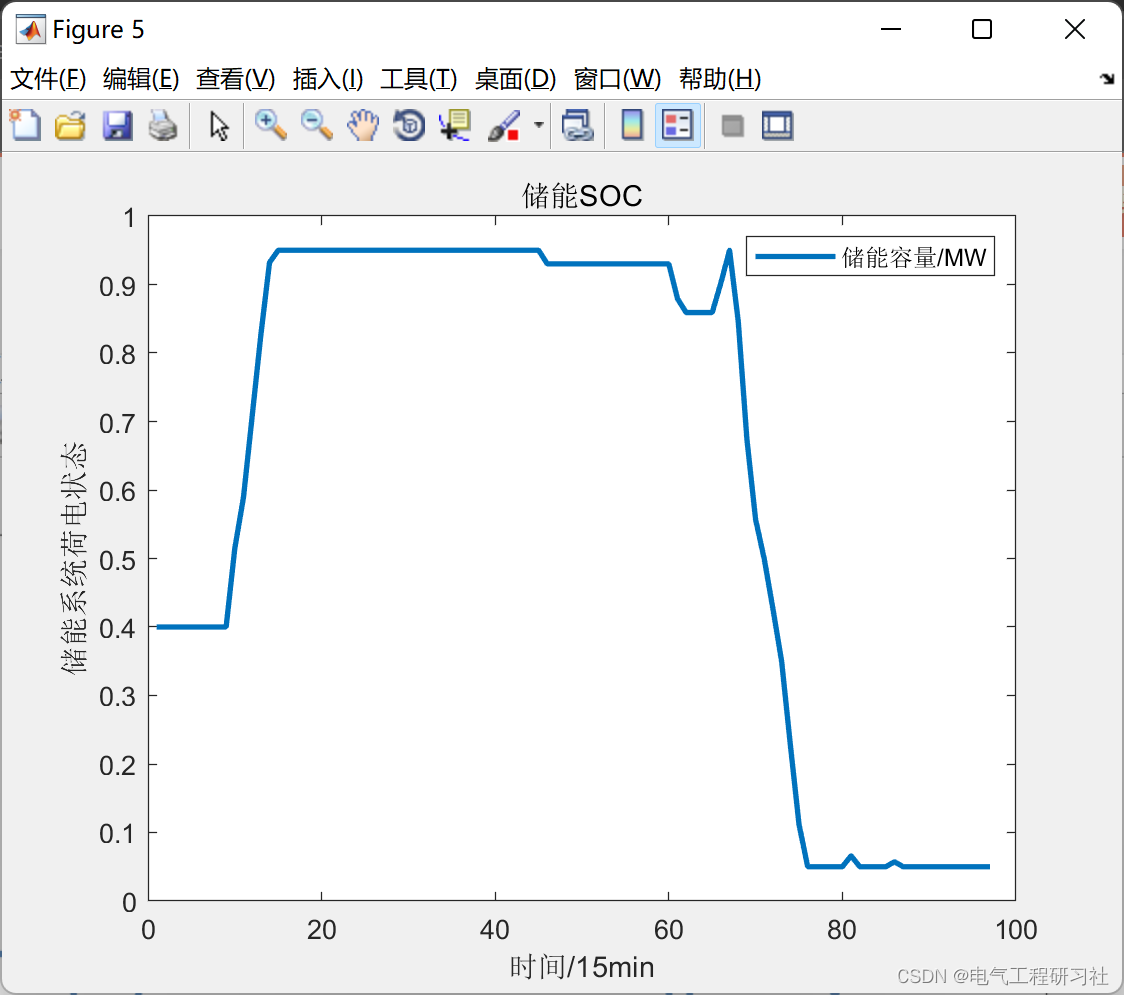
此时机组日发电计划曲线如图5.1所示，

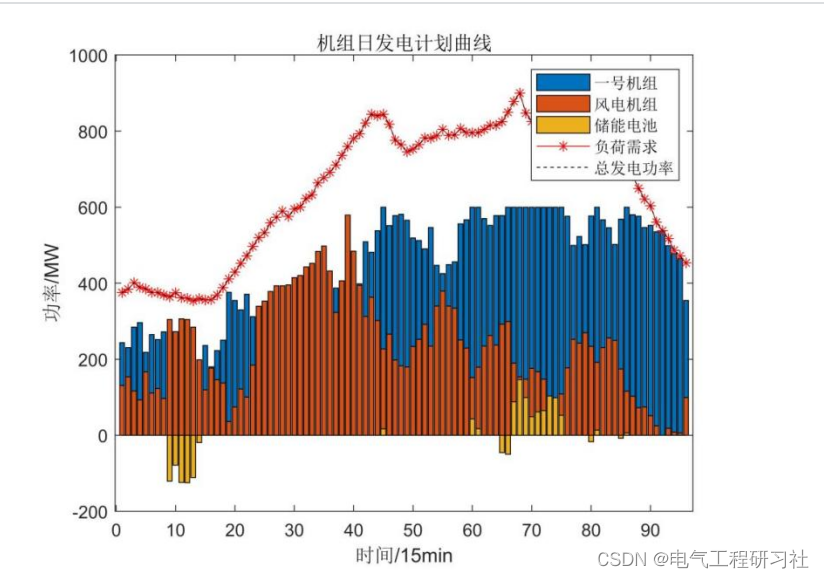
图5.1

图5.2

图5.3

有14个时段存在弃风的情况，弃风电量达到570.938MWh，不存在失负荷的情况。

考虑储能成本、单位碳捕捉成本（取60元/t），此时系统单位供电成本见表8

表8 风电装机900MW替代机组2、3且配置储能时系统相关指标统计

结果分析：储能是解决高比例风电消纳问题、提高系统可靠性的有效手段。然而负荷曲线与风电出力曲线都会影响储能的配置结果。通过配置合适的储能容量，可以减少风电的弃风和失负荷。

 

 

 

第五题需要代码点这里：🍞正在为您运送作品详情

6 第六题：

6.1.当负荷功率不变，由2-5题可知，当风电替代容量递增时，在风电可发电功率很小的时段，需要火电机组保持很高的发电功率甚至满载功率以尽可能的向系统供电，但仍然会出现失负荷的现象。且随着风电替代容量的增加，失负荷电量也再增加，并且系统备用容量变少，可靠性降低。

6.2.为保障可靠供电，考虑配置储能设备。在之前弃风的时段，用风电对储能进行放电，在风电功率低谷时段，通过储能和火电同时供电，为系统保留了部分备用用量，以应对特殊情况。风电装机900MW替代机组2、3的场景下，增加配置储能，此时供电系统单位供电成本有降低。

根据观察表4和表5可得，弃风损失减少了20%，更关键的是新增加的储能成本远低于不配置储能时失负荷的损失，只是失负荷的损失的52%。所以在新能源占比高的电力系统中配置储能，能更好的保证供电可靠性，同时，相比于不装储能时切负荷的损失，配置储能更具经济性。储能作为优质的灵活调节资源，可以在不同时间尺度提供多种价值的服务，必然伴随着新能源发电同步发展。

6.3.分别针对风电替代机组 3 、替代机组2、替代机组 2和3的三种场景下，考虑配置储能，为保障可靠供电，以最小发电成本为目标函数，求配置的储能容量和系统发电成本。

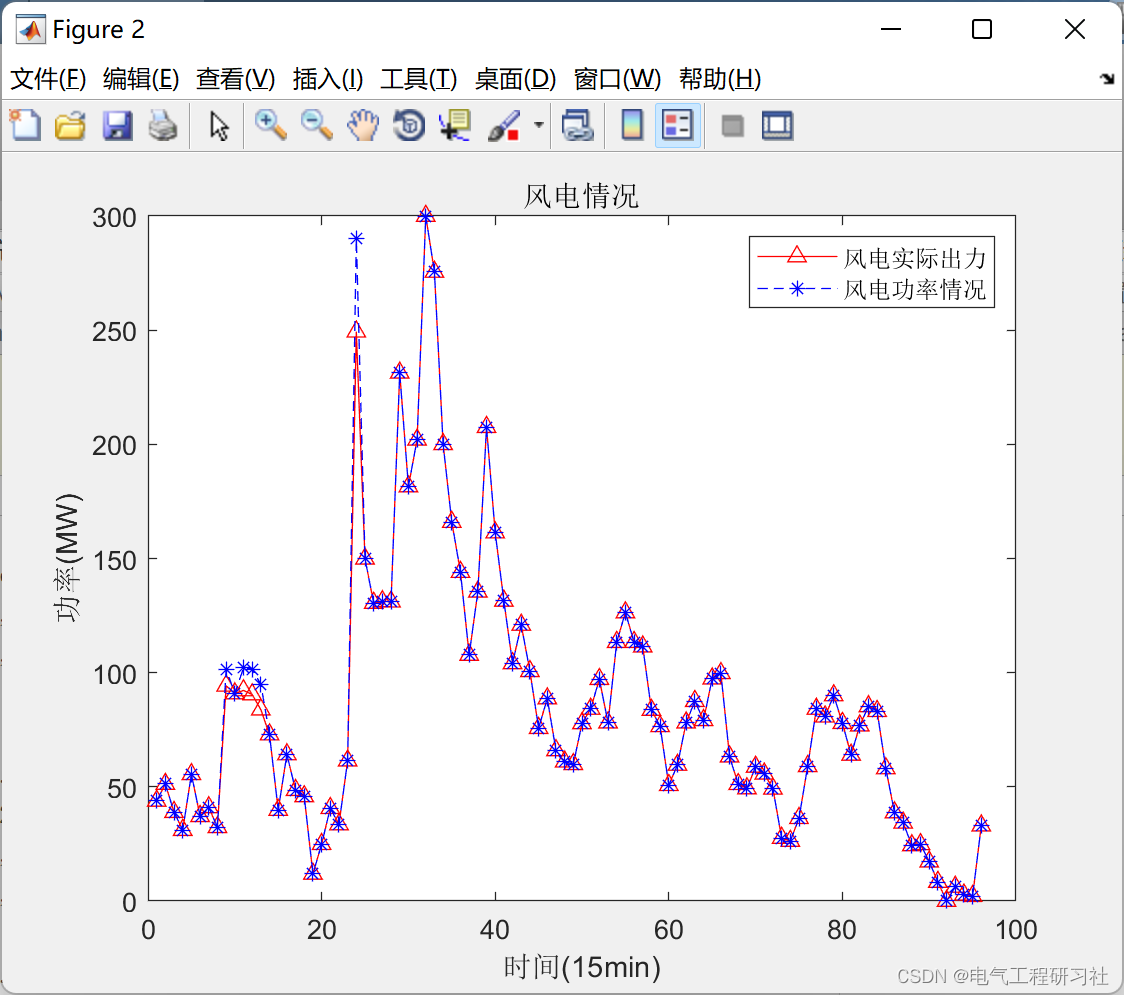
6.3.1.此时求得的结果为，（1）风电装机 300MW、替代机组3时，不需要配置储能，此时机组日发电计划曲线见图2.2（1）；（2）风电装机 600MW、替代机组2时，配置储能60.515MW，此时机组日发电计划曲线如图6.3.1；（3）风电装机 900MW、替代机组 2、3 时，配置储能944.420MW，此时机组日发电计划曲线见图5.1。

图6.3.1

其实系统单位成本如表9所示

表9不同风电替代容时系统相关指标统计

风电装机 600MW、替代机组2时，配置储能相比不配置储能的情况，系统单位供电成本由0.176增加到0.207，增加了18%；风电装机 900MW、替代机组 2、3 时，配置储能相比不配置储能的情况，系统单位供电成本由0.26减少到0.209，降低了20%。在风电占比不高的情况下，投资储能的成本较高，增加了系统单位供电成本。但是在未来风电清洁能源占比高的系统中，增加配置储能，减少失负荷的损失，可以达到降低系统单位供电成本的效果。

 

 

 

 

 

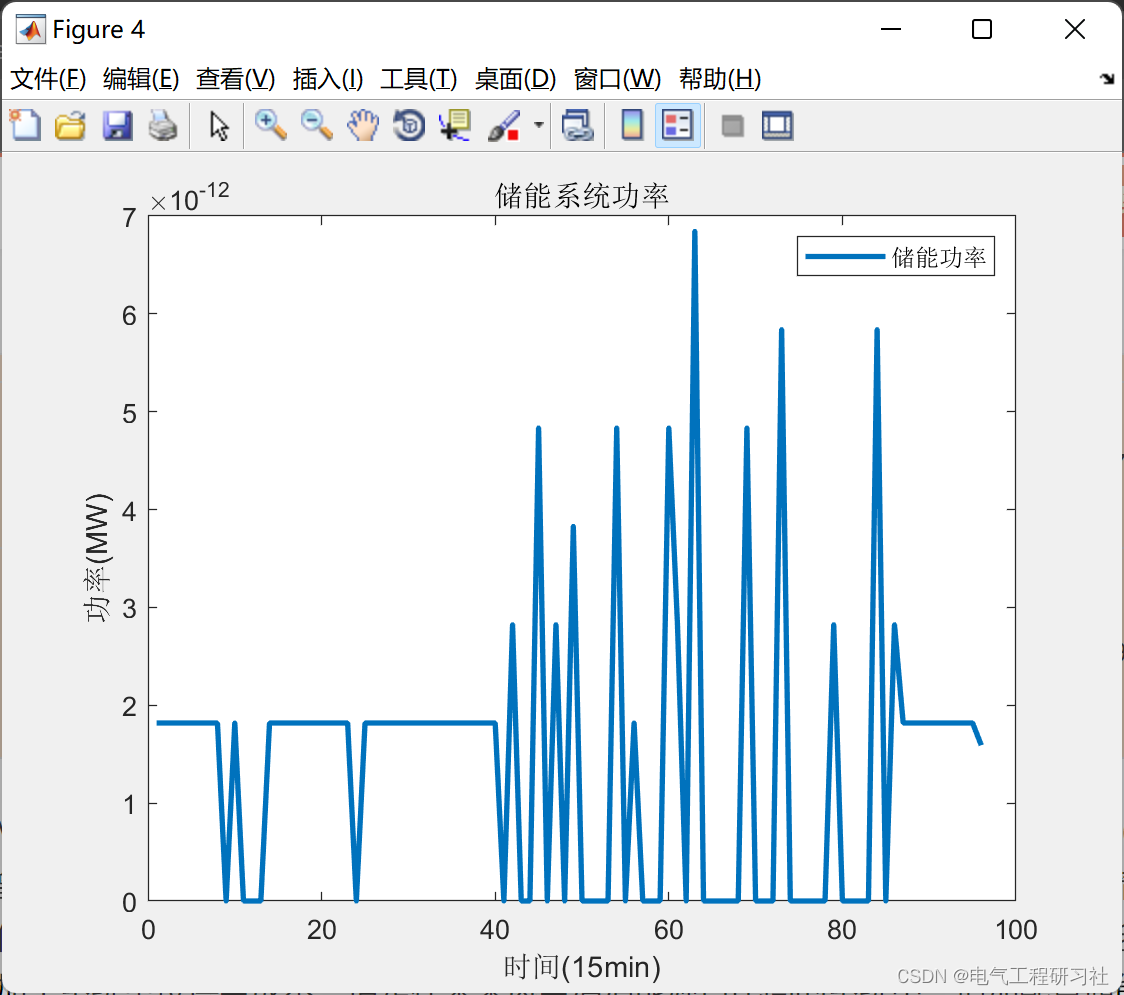
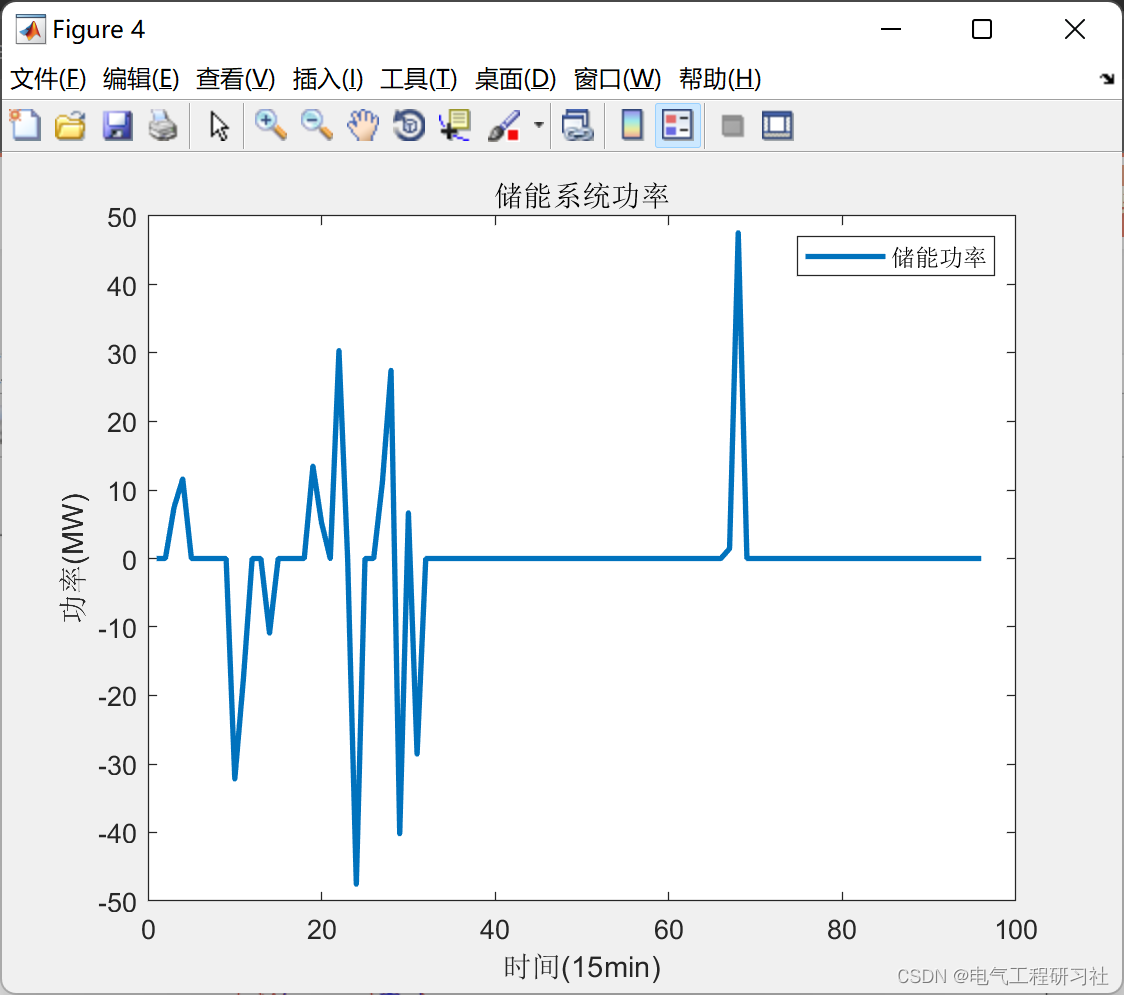
 第六题代码需要点这里：🍞正在为您运送作品详情

7 第七题：

7.1.针对附件2所示的十五天负荷功率（最大值1200MW）、风电功率（装机容量1200MW），在风电替代火电机组 2、3场景下，系统功率平衡存在的问题。

我们拿第一天和风能最少的第8天为例子，根据最小发电成本为目标函数，绘制机组日发电计划曲线如下图，

 

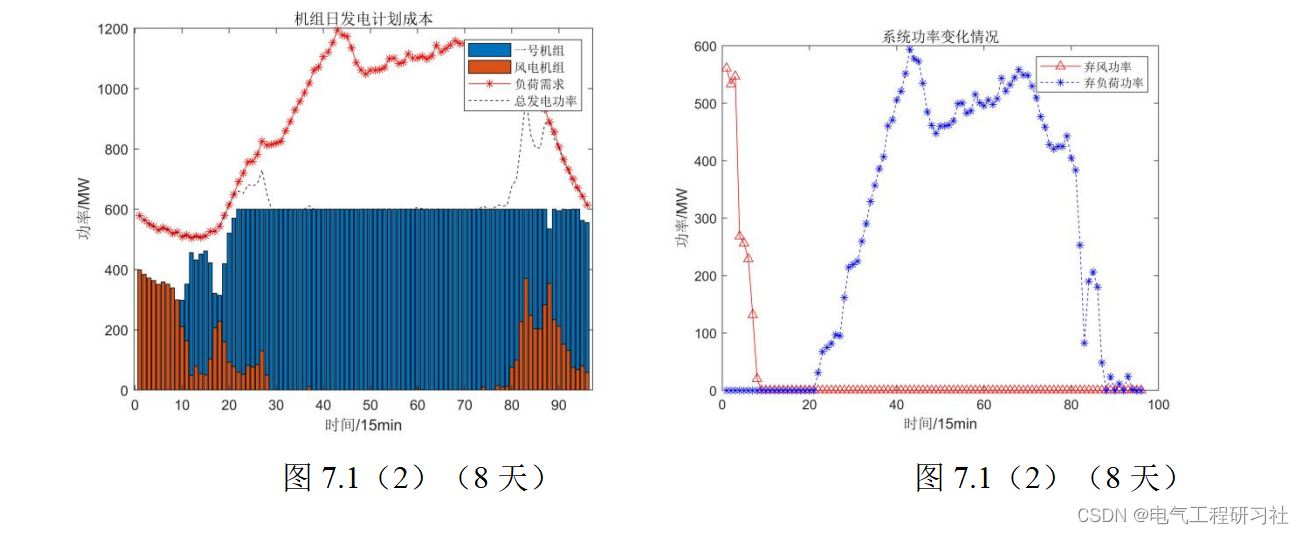
由于天气原因，在15天一个周期内，风能变化大风力发电功率波动也大，存在大范围弃风和弃负荷的现象。

表10第一天时系统相关指标统计

由于当前储能系统成本较高，如何合理地配置储能系统容量，在保证系统安全稳定运行的前 提下，尽可能减少储能系统的投资成本显得尤为 重要。

为解决功率平衡解决方案，我们考虑配置储能。在问题五中，由于只考虑一天内的最优化调度问题，本文未对储能系统一天调度周期结束时的剩余荷电状态进行约束限制，因此问题五中储能系统在一天结束时的荷电状态已降至最低，如图5.1所示。而当调度周期由一天变为十五天时，则需要考虑储能系统在两天之间的衔接关系，在前一天结尾时不能将所剩的电量用尽，这是为了使储能系统的荷电状态仍然保持在一定的水平，以便满足后一天调度周期内储能系统的调度可行性。

一般来说，储能系统一天调度周期结束时的剩余荷电状态经常被约束条件设置在40-60%之间，但通过观察本题所提供的十五天负荷及风电曲线可知（这里可以加一张15天内的负荷和风电图），风电在前六日的发出功率较为充沛，而在第七日和第八日左右出现枯竭的情况，此时火电机组即使满功率运行也无法满足实际负荷的需求。综上考虑，本文将储能系统一天调度周期结束时的剩余荷电状态设置为20%-90%，这使储能系统在十五天的调度周期中拥有更加灵活且经济的运行方式，如此大的剩余荷电状态范围设置大允许储能系统在风电充沛的时间段内存储足够的电量，以应对风电匮乏的时间段，最大程度上保障了供电的可靠性与经济性。

7.2.1.先优先考虑保证供电可靠，然后选择配置储能容量的方案。此时选择的储能容量为70000MW。

图7.2.1（1）

图7.2.1（2）

图7.2.1（3）

SOC表示储能系统在一天调度周期内的剩余电量的变化图

表 11

单位供电成本为0.308元/kWh，相比于不加储能的0.700元/kWh，降低了57%，经济性来说，还说挺好。

7.2.2.考虑可以切负荷来解决功率平衡，即考虑失负荷损失，重新确定配置的储能容量方案。此时选择的储能容量为15984MW。

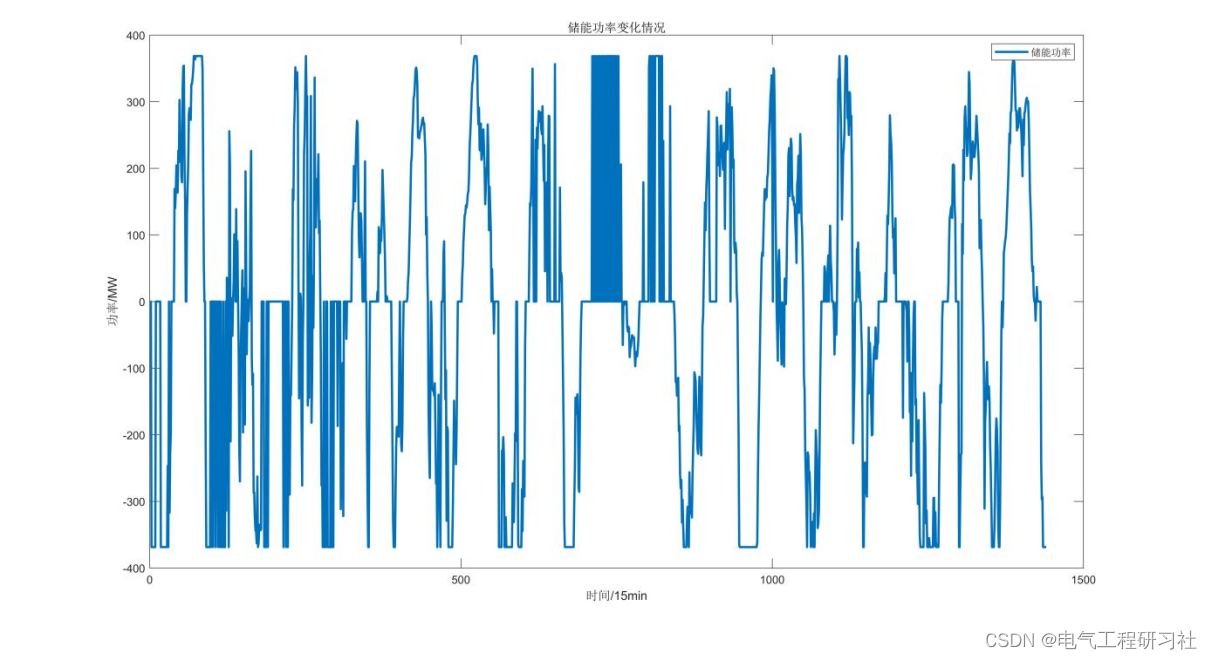
此时发电成本如表12所示，

表 12

考虑可以切负荷的情况下，增加配置储能，就降低了单位供电成本。

7.2.仅仅靠配置储，在不考虑储能成本的条件下，通过增加储能容量，能保证功率平衡，也能提高风电接入的可靠性，但是经济性会降低，单位供电成本会增加50%左右。如果考虑可切负荷的情况，配置储能就能够提高经济性，降低单位供电成本。

 

 

 

 

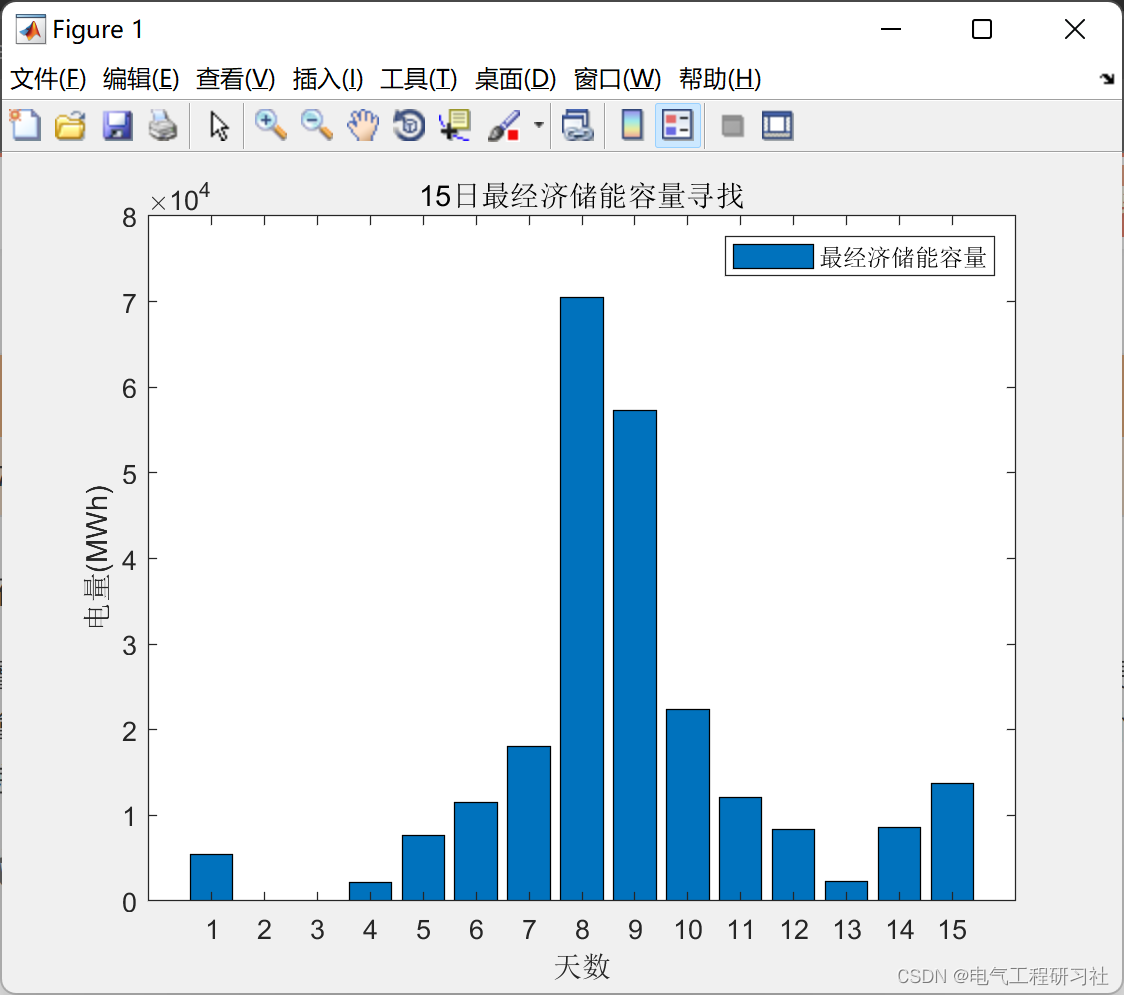
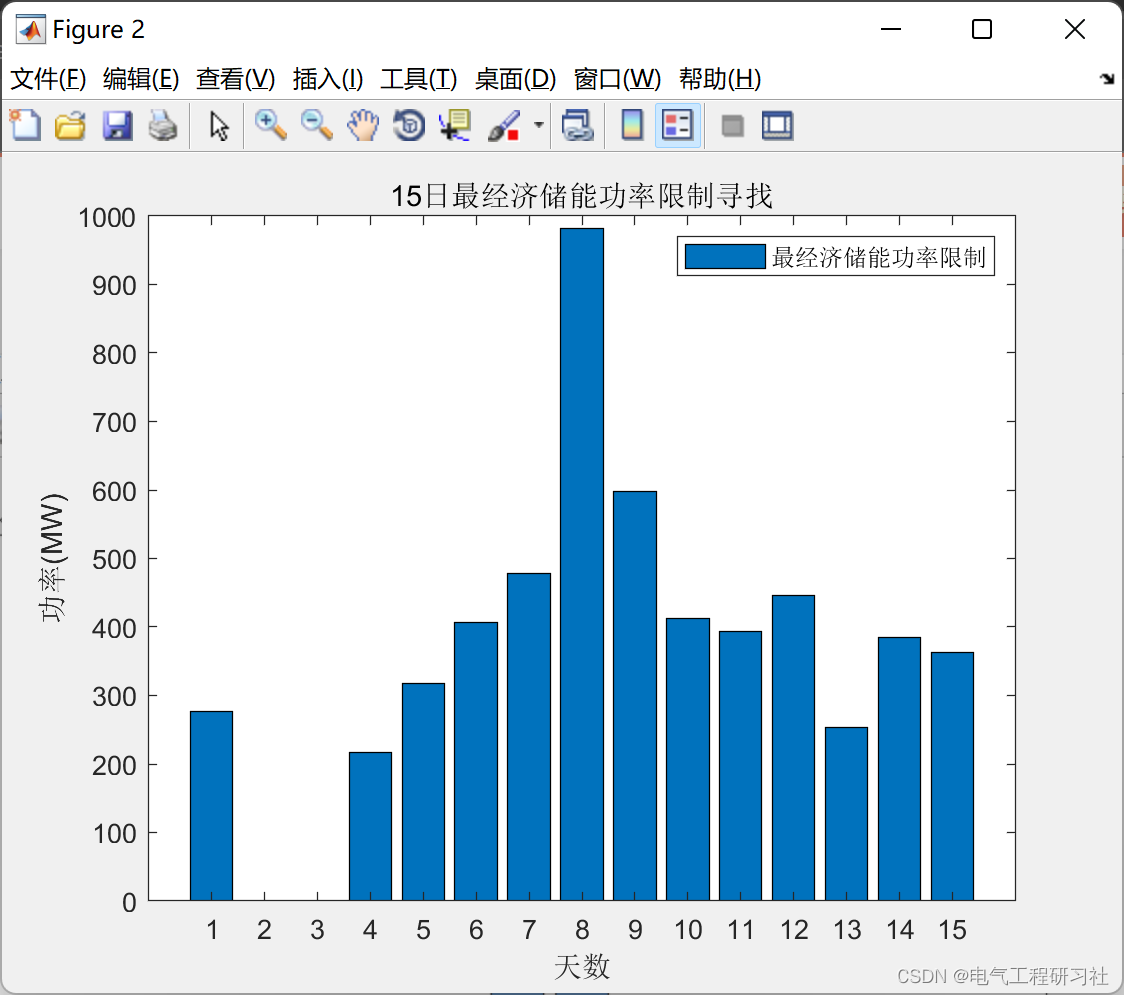
 需要第七题所有代码点这里：🍞正在为您运送作品详情

8 所有题代码及文章详细讲解

需要打包带走点这里： 高比例风电电力系统储能运行及配置分析（Matlab实现） (mianbaoduo.com)

9 结论：

1）新能源的接入对于系统发电运行成本的改变；火电厂的碳捕集是一笔很大的费用，新能源具备低碳,节能,环保的可再生特点，在本文中，只考虑风力机组的运维成本，能很大程度降低系统发电的运行成本。同时，可以通过合理弃风放弃部分风电发电容量来改系统发电运行成本，

2）配置储能可有效消纳风电，系统配置储能时应重点考虑分时电价与风电装机容量等因素。加入储能装置后，火电机组需长时间维持在较高发电功率的情况得到了的改善，系统内能量达到更优配置，有利于电力系统安全运行。储能在初期的投资成本比较大，但是后期运维费用很低。

10 参考文献

[1]刘新东,方科,陈焕远,佘彩绮.利用合理弃风提高大规模风电消纳能力的理论研究[J].电力系统保护与控制,2012,40(06):35-39.

[2]2017-2021年中国弃风量及弃风率年度变化统计情况_观研报告网2017-2021年中国弃风量及弃风率年度变化统计情况_观研报告网 (chinabaogao.com)

[3]王淑云,娄素华,吴耀武,曹侃,周鲲鹏.计及火电机组深度调峰成本的大规模风电并网鲁棒优化调度[J].电力系统自动化,2020,44(01):118-125.