• TinyRenderer学习笔记--从零构建软件渲染器

    开始软件渲染器–tinyrenderer的学习

    文章目录


    原项目地址 https://github.com/ssloy/tinyrenderer

    参考文档从零构建光栅器，tinyrenderer笔记（上） - 知乎 (zhihu.com)(非常不错！)

    使用软件 vs2022，ps2019(查看TGA图片)

    1、准备工作

    首先，我们需要设置像素的颜色的功能

    struct TGAColor 
{
	union 
	{
		struct 
		{
			unsigned char b, g, r, a;//四色
		};
		unsigned char raw[4];
		unsigned int val;

	};
	int bytespp;
	
	TGAColor():val(0),bytespp(1){}
	
	TGAColor(unsigned char R, unsigned char G, unsigned char B, unsigned char A) : b(B), g(G), r(R), a(A), bytespp(4) {
	}
	
	TGAColor(int v, int bpp) : val(v), bytespp(bpp) {
	}
	
	TGAColor(const TGAColor& c) : val(c.val), bytespp(c.bytespp) {
	}
	
	TGAColor(const unsigned char* p, int bpp) : val(0), bytespp(bpp) {
		for (int i = 0; i < bpp; i++) {
			raw[i] = p[i];
		}
	}
	
	TGAColor& operator =(const TGAColor& c)
	{
		if (this != &c)
		{
			bytespp = c.bytespp;
			val = c.val;
		}
		return *this;
	}

};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42

    此结构体可以储存颜色的三个分量信息的透明度信息。

    下面这是关于TGA文件的相关操作，不是此次课程的重点，不再解释，有需求可查看项目源码。

    class TGAImage {
protected:
	unsigned char* data;
	int width;
	int height;
	int bytespp;

	bool   load_rle_data(std::ifstream& in);
	bool unload_rle_data(std::ofstream& out);

public:
	enum Format {
		GRAYSCALE = 1, RGB = 3, RGBA = 4
	};

	TGAImage();
	TGAImage(int w, int h, int bpp);
	TGAImage(const TGAImage& img);
	bool read_tga_file(const char* filename);
	bool write_tga_file(const char* filename, bool rle = true);
	bool flip_horizontally();
	bool flip_vertically();
	bool scale(int w, int h);
	TGAColor get(int x, int y);
	bool set(int x, int y, TGAColor c);
	~TGAImage();
	TGAImage& operator =(const TGAImage& img);
	int get_width();
	int get_height();
	int get_bytespp();
	unsigned char* buffer();
	void clear();

};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34

    Lesson 1、学习Bresenham’s Line Drawing Algorithm

    ，用于在计算机中绘制直线段，其计算简单，仅仅只用了整数加法、减法和位移法。

    我们尽量把精力放在渲染器的实现上，所以要尽可能减少对外部库的依赖，此次的实验只会涉及TGA文件的使用。

    Vision 1

    void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color)
{
	for (float t = 0; t < 1; t += 0.1)
	{
		int x = x0 + (x1 - x0) * t;
		int y = y0 + (y1 - y0) * t;
		image.set(x, y, color);
	}
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9

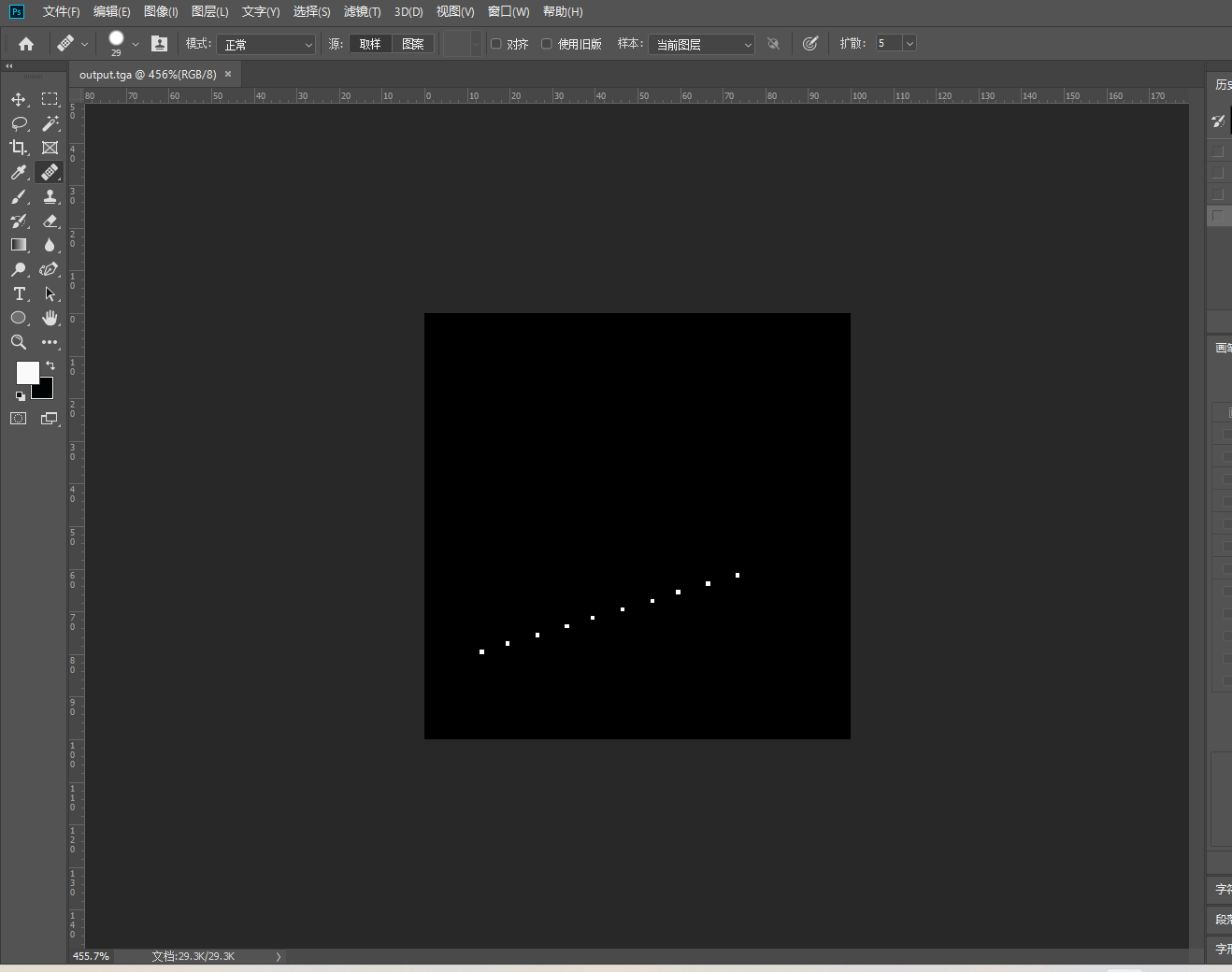
    image-20220812115624365

    显然，这段代码只是输出了此线段上的某些像素点而已，如果我们要近似地得到整个线段，就需要将t设置成很小的值，会增加性能消耗。

    Vision 2

void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color)
{
	for (int x = x0; x <= x1; x++)
	{
		float t = (x - x0) / (float)(x1 - x0);
		int y = y0 * (1. - t) + y1 * t;
		image.set(x, y, color);
	}
}
line(13, 20, 80, 40, image, white); 
line(20, 13, 40, 80, image, red); 
line(80, 40, 13, 20, image, red);

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14

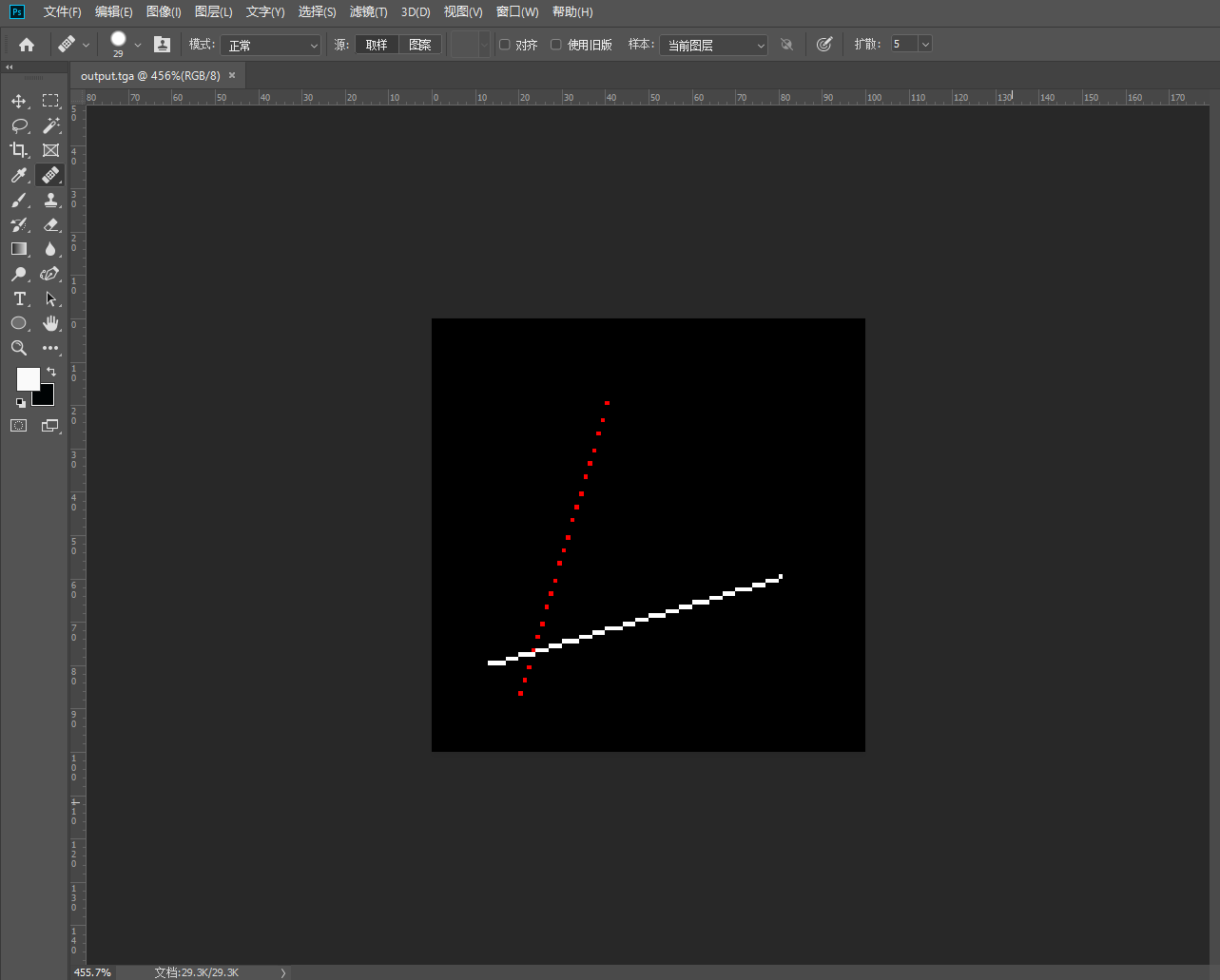
    image-20220812120914731

    可以看出，第二条线和第三条线是有问题的，第二条线有空隙，第三条线没有绘制出来。第二条线的错误很明显，Y的改变速率远比X大，导致出现了空隙，有的点没有被绘制出来；第三条线的错误在于我们的代码默认了X1>X0，而第三条线不满足这个条件，导致线段不会被绘制出来。

    Vision 3

    void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color)
{
	bool steep = false;
	if (std::abs(x0 - x1) < std::abs(y0 - y1))
	{
		//直线斜率太大，需要翻转
		std::swap(x0, y0);
		std::swap(x1, y1);
		steep = true;
	}
	if (x0 > x1)
	{
		//保证x1比x0大，否则t会出现负值
		std::swap(x0, x1);
		std::swap(y0, y1);
	}
	for (int x = x0; x <= x1; x++)
	{
		float t = (x - x0) / (float)(x1 - x0);
		int y = y0 * (1. - t) + y1 * t;
		if (steep)
		{
			image.set(y, x, color);//翻转回来
		}
		else
		{
			image.set(x, y, color);
		}
	}
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30

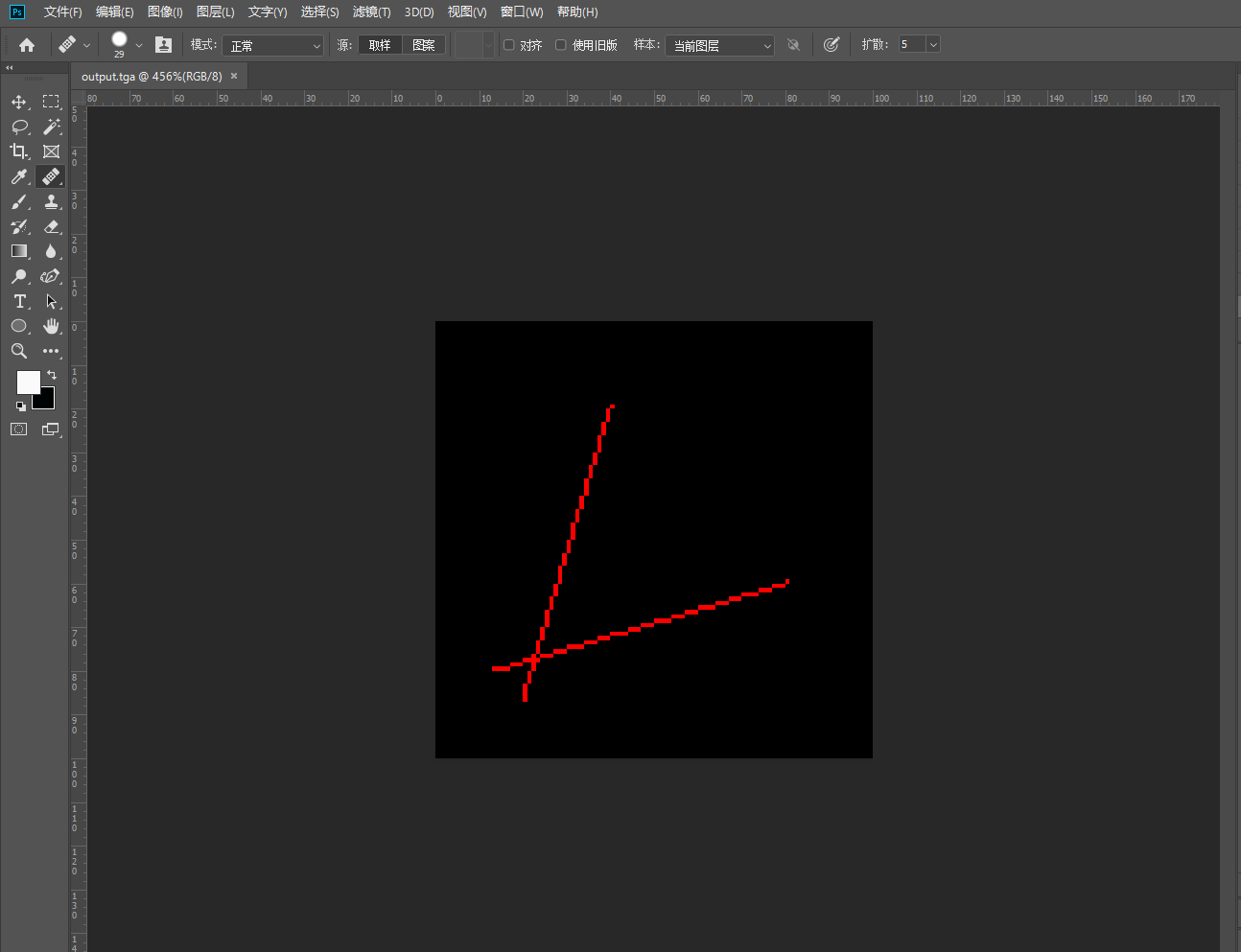
    image-20220812123116828

    此版本解决了Vision 2的两个问题

    Vision 4 最终版

    void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color)
{
	bool steep = false;
	if (std::abs(x0 - x1) < std::abs(y0 - y1))
	{
		//直线斜率太大，需要翻转
		std::swap(x0, y0);
		std::swap(x1, y1);
		steep = true;
	}
	if (x0 > x1)
	{
		//保证x1比x0大，否则t会出现负值
		std::swap(x0, x1);
		std::swap(y0, y1);
	}
	int dx = x1 - x0;
	int dy = y1 - y0;
	int derror2 = std::abs(dy) * 2;
	int error2 = 0;
	int y = y0;
	for (int x = x0; x <= x1; x++)
	{
		if (steep)
		{
			image.set(y, x, color);//翻转回来
		}
		else
		{
			image.set(x, y, color);
		}
		error2 += derror2;
		if (error2 > dx)
		{
			y += (y1 > y0 ? 1 : -1);
			error2 -= dx * 2;
		}
	}
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39

    这个版本对上一个版本进行了优化，上一个版本已经可以使用了，但是不够高效。在Vision 4中，我们用误差变量来代替重复的除法运算，根据误差的大小来判断下一个x对于的y值要如何变化。另外通过数学办法来消除了含有浮点数的运算（这里我还没咋看懂是怎样变化的，可以查看https://supercodepower.com/docs/toy-renderer/day2-draw-line）

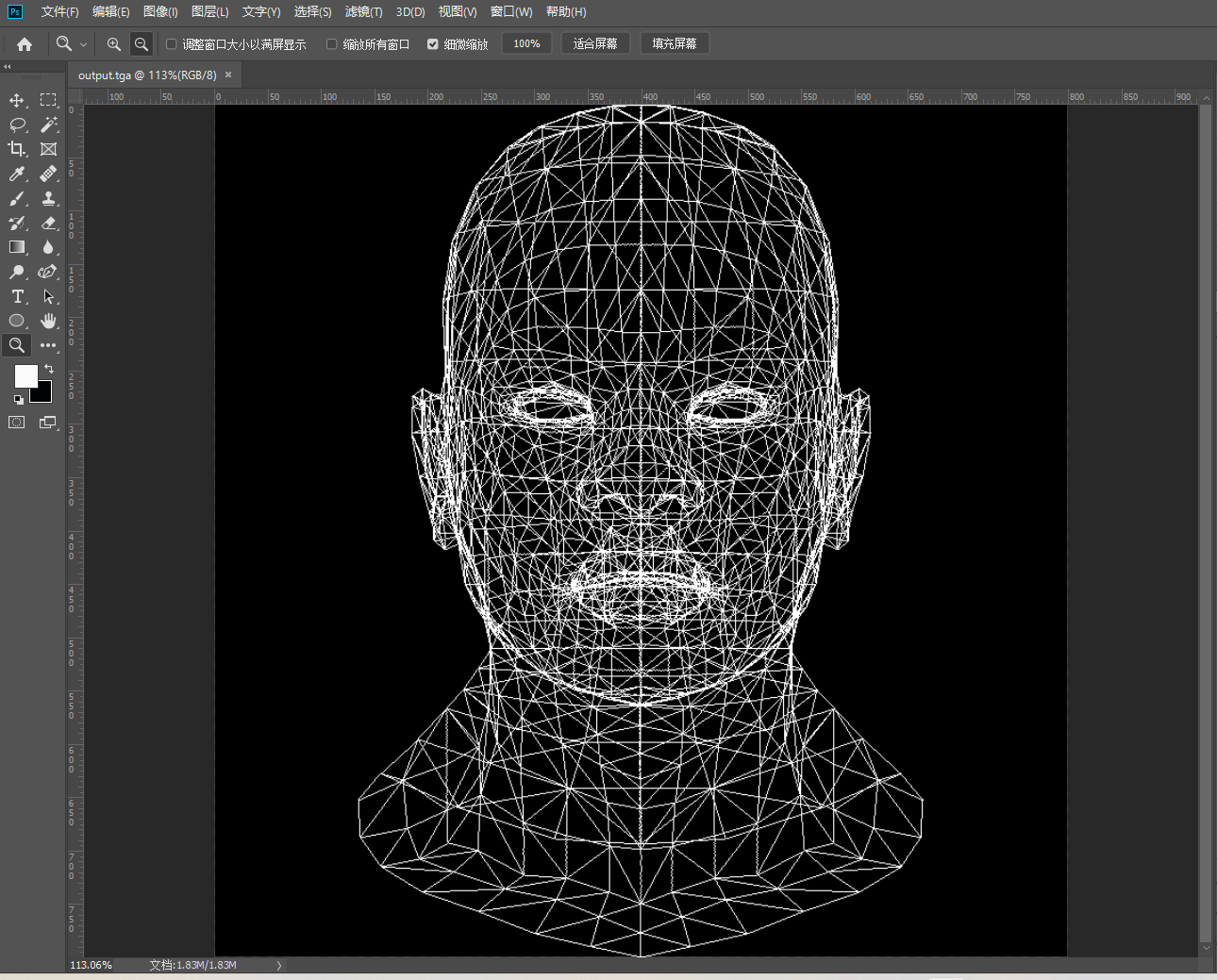
    下面我们使用项目提供的文件来绘制人脸，在使用obj文件之前，我们还需要其他项目文件，例如几何处理等，这里我们并不关心其内部是如何实现的

    image-20220812161046121

    最后产生的图片是

    image-20220812165923376

    Lesson 2、三角形栅格化和背面剔除

    经过上一节的探讨，现在我们已经可以绘制两个点之间的一条线段，现在我们需要绘制一个三角形，这很简单，绘制三条线段，首尾相连即可。

    void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage& image, TGAColor Color)
{
    line(t0, t1, image, Color);
    line(t1, t2, image, Color);
    line(t2, t0, image, Color);
}
    Vec2i t0[3] = { Vec2i(10, 70),   Vec2i(50, 160),  Vec2i(70, 80) };
    Vec2i t1[3] = { Vec2i(180, 50),  Vec2i(150, 1),   Vec2i(70, 180) };
    Vec2i t2[3] = { Vec2i(180, 150), Vec2i(120, 160), Vec2i(130, 180) };
   
    triangle(t0[0], t0[1], t0[2], image, red);
    triangle(t1[0], t1[1], t1[2], image, white);
    triangle(t2[0], t2[1], t2[2], image, green);

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13

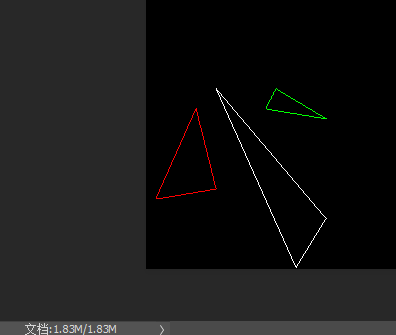
    image-20220813110342964

    很好，现在我们已经可以绘制出三角形了，但是我们还需要进行栅格化，也就是把三角形进行填充，相信有了前面的经验，这里也能很快想到办法，就是扫线法。按照教程，我们需要把三角形分成两个部分来绘制，这样就需要对三角形的点进行预处理，t0>t1>t2，从t1顶点划水平线来分割三角形

    void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage& image, TGAColor Color)
{
    if (t0.y > t1.y) std::swap(t0, t1);
    if (t0.y > t2.y) std::swap(t0, t2);
    if (t1.y > t2.y) std::swap(t1, t2);
    int total_height = t2.y - t0.y;
    for (int y = t0.y;y <= t1.y; y++)
    {
        int segment_height = t1.y - t0.y+1;
        float alpha = (float)(y - t0.y) / total_height;
        float beta = (float)(y - t0.y) / segment_height;
        Vec2i A = t0 + (t2 - t0) * alpha;
        Vec2i B = t0 + (t1 - t0) * beta;
        if (A.x > B.x)std::swap(A, B);
        for (int x = A.x;x <= B.x; x++)
        {
            image.set(x, y, Color);
        }
    }
    for (int y = t1.y; y <= t2.y; y++)
    {
        int segment_height = t2.y - t1.y + 1;
        float alpha = (float)(y - t0.y) / total_height;
        float beta = (float)(y - t1.y) / segment_height;
        Vec2i A = t0 + (t2 - t0) * alpha;
        Vec2i B = t1 + (t2 - t1) * beta;
        if (A.x > B.x)std::swap(A, B);
        for (int x = A.x; x <= B.x; x++)
        {
            image.set(x, y, Color);
        }
    }
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33

    这段代码就可以对一个三角形进行栅格化填充，将三角形分成两个部分，分别使用扫线法进行填充。

    image-20220813120949110

    void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage& image, TGAColor Color)
{
    if (t0.y > t1.y) std::swap(t0, t1);
    if (t0.y > t2.y) std::swap(t0, t2);
    if (t1.y > t2.y) std::swap(t1, t2);
    int total_height = t2.y - t0.y;
    for (int i = 0; i <= total_height; ++i)
    {
        bool second_half = i > t1.y - t0.y || t1.y == t0.y;
        int segment_height = (second_half ? t2.y - t1.y : t1.y - t0.y) + 1;
        float alpha = (float)i / total_height;
        float beta = (float)(second_half?i-(t1.y-t0.y):i) / segment_height;
        Vec2i A = t0 + (t2 - t0) * alpha;
        Vec2i B = second_half? t1 + (t2 - t1) * beta: t0 + (t1 - t0) * beta;
        if (A.x > B.x)std::swap(A, B);
        for (int x = A.x; x <= B.x; x++)
        {
            image.set(x, i+t0.y, Color);
        }
    }
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21

    上面的代码是对原始的三角形栅格化代码进行了整理，原来的代码有大量的重复的部分，改进的代码使用了标志变量，让代码更加简洁。至此，我们已经可以绘制出线段、三角形，并可以填充三角形了。上面的填充三角形的办法有点古老，尽管其是准确的，下面我们将会探讨其他的填充方法。

    上面的代码是找到每一个在三角形内部的像素点，然后进行绘制，我们新的方法将会处理更多的像素点，包括一些不在三角形内部的点，对于现代计算机来说，多的这些点产生的额外的性能消耗可以忽略不计。具体方法是找到三角形的最小包围盒，包围盒就是能把三角形完全包含起来的矩形框，然后对包围盒里面的点进行判断，判断其是否在三角形内部，判断方法使用**重心坐标。**关于重心坐标可以查看百科，games101也有相关介绍。

    //求重心坐标
Vec3f barycentric(Vec3f A, Vec3f B, Vec3f C, Vec3f P)
{
    //利用叉积计算P点的重心坐标
    Vec3f k = Vec3f(C.x - A.x, B.x - A.x, A.x - P.x) ^ Vec3f(C.y - A.y, B.y - A.y, A.y - P.y);
    //三点共线时
    if (std::abs(k.z) <1)
    return Vec3f(-1, 1, 1);
    //返回归一化的重心坐标
    return Vec3f(1.f - (k.x + k.y) / k.z, k.x / k.z, k.y / k.z);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    void triangle(Vec3f* pts, TGAImage& image, TGAColor color)
{
    //声明包围盒，并给予初始值
    Vec2f bboxmin(std::numeric_limits::max(), std::numeric_limits::max());
    Vec2f bboxmax(-std::numeric_limits::max(), -std::numeric_limits::max());
    Vec2f clamp(image.get_width() - 1, image.get_height() - 1);
    for (int i = 0; i < 3; ++i)
    {
        //确定包围盒
        bboxmin.x = std::max(.0f, std::min(bboxmin.x, pts[i].x));
        bboxmin.y = std::max(.0f, std::min(bboxmin.y, pts[i].y));
        //第一个max和min只是为了确保包围盒的合法性
        bboxmax.x = std::min(clamp.x, std::max(bboxmax.x, pts[i].x));
        bboxmax.y = std::min(clamp.y, std::max(bboxmax.y, pts[i].y));
    }
    Vec3f p;//临时储存包围盒里的每一个像素坐标
    for (p.x = bboxmin.x; p.x <= bboxmax.x; p.x++)
    {
        for (p.y = bboxmin.y; p.y <= bboxmax.y; p.y++)
        {
            //遍历包围盒
            //获取P的重心坐标
            Vec3f u = barycentric(pts[0], pts[1], pts[2], p);
            //判断是否在三角形内，不在就不做操作，在就将其像素染色
            if (u.x < 0 || u.y < 0 || u.z < 0) continue;
            image.set(p.x, p.y, color);
        }
    }
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29

    最后效果如下：

    image-20220813161759164

    在上一节我们已经能够利用obj文件来绘制三角形网格模型，这节我们又学习了三角形的填充，所以现在对上一节的网格模型进行填充

    for (int i = 0; i < model->nfaces(); i++) {
    std::vector face = model->face(i);
    Vec2f screen_coords[3];//屏幕坐标

    for (int j = 0; j < 3; ++j)
    {
        Vec3f v = model->vert(face[j]);//世界坐标
        screen_coords[j] = Vec2f((v.x + 1.) * width / 2., (v.y + 1.) * height / 2.);
    }
    triangle(screen_coords, image, TGAColor(rand() % 255, rand() % 255, rand() % 255, 255)); 
} 

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11

    image-20220813200723841

    看起来比单纯的网格模型要绚烂许多了，但是面部细节没有，接下来我们需要根据简单的光照原理来进行绘制。我们可以知道的是，光照射到平面上，平面接受的光越多，根据能量守恒定律，光强越小，光越暗，这里我们使用理想的平行光源，不考虑光的衰减，那么平面反射的光就只和平面被照射到的面积有关，而被照射到的面积又与平面和平行光的夹角有关，要知道夹角，就要知道三角形平面的法向量。

    至此，我们找到了展现阴影的关键，就是要计算平面的法向量，然后用法向量和光源相乘，就能得到相应的光强。不同的光强就能展示出阴影的效果。

    Vec3f light_dir(0, 0, -1);


    for (int i = 0; i < model->nfaces(); i++) {
        std::vector face = model->face(i);
        Vec2i screen_coords[3];//屏幕坐标
        Vec3f world_coords[3];//世界坐标
    
        for (int j = 0; j < 3; ++j)
        {
            Vec3f v = model->vert(face[j]);
            screen_coords[j] = Vec2i((v.x + 1.) * width / 2., (v.y + 1.) * height / 2.);
            world_coords[j] = v;
        }
        //使用世界坐标来计算法向量
        Vec3f n = (world_coords[2] - world_coords[0]) ^ (world_coords[1] - world_coords[0]);
        n.normalize();
        //计算光照强度，即法向量乘以光照方向
        float intensity = n*light_dir;
        //光照强度大于0才能被检测到，小于0的是在背光面，观察不到，不用绘制，即背部剔除
        if (intensity > 0)
        {
            triangle(screen_coords, image, TGAColor(intensity * 255, intensity * 255, intensity * 255, 255));
        }
    } 



    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27

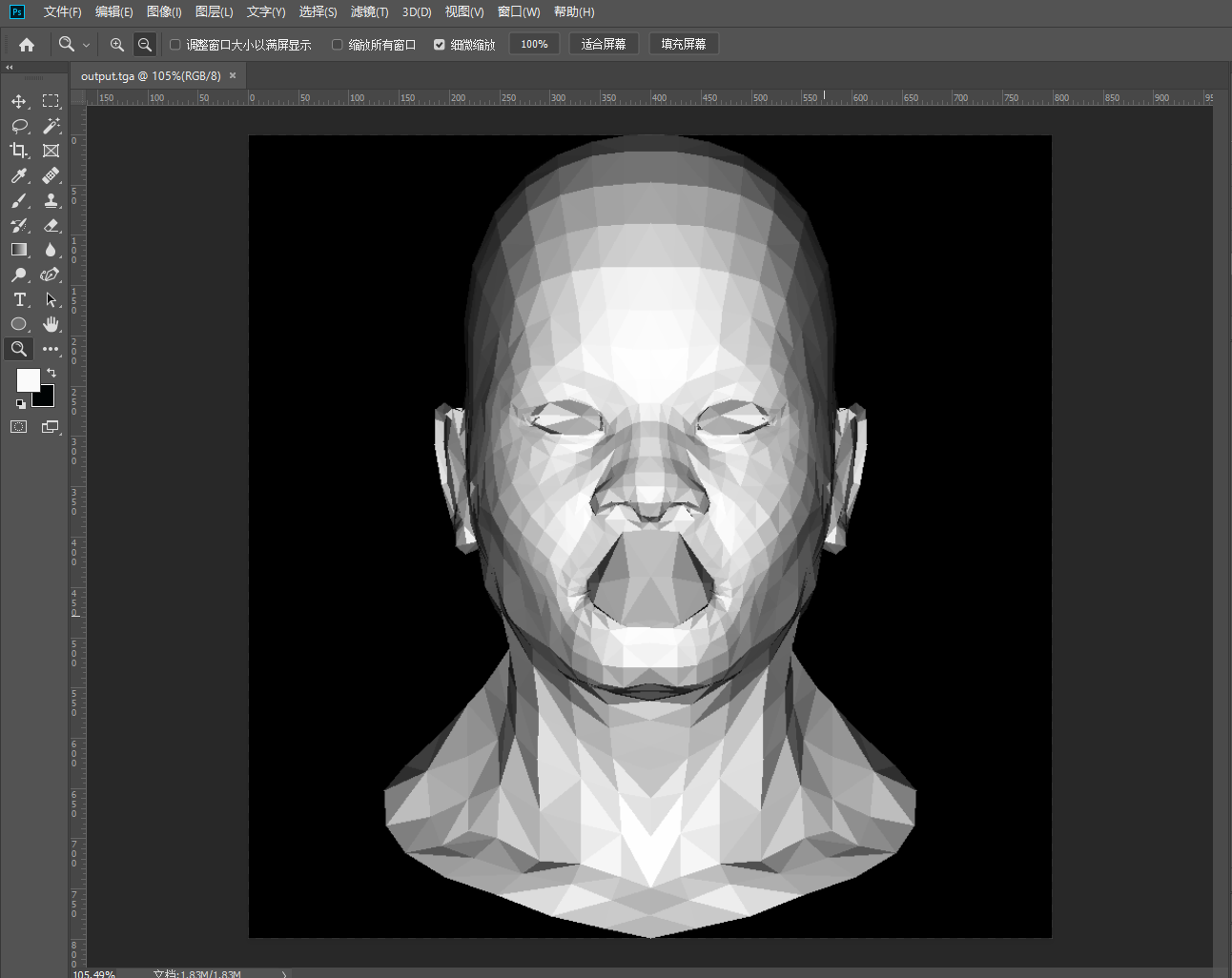
    image-20220813205527213
    好，到这里我们此次课程的前两课就结束喽，后面的课程会以两节为一次来学习。

  • 相关阅读:
    思科华为设备DHCP配置命令对比
    Go 学习之 io.Reader 从源码了解如何编写
    【AI】PyTorch实战（一）：目标检测之fasterrcnn_resnet50_fpn
    mysql主从架构
    FTX和Binance摩擦升级？一文梳理“吵架”背后始末
    前后台同一个端口部署项目
    低代码编辑平台后台实现
    纹波类型及纹波抑制措施
    如何写一份全面、易读的交互说明文档
    GeoServer安装以及部署
  • 原文地址：https://blog.csdn.net/qq_51599283/article/details/126324338