-
因子分析模型介绍、matlab案例我国上市公司盈利能力与资本结构的实证分析
因子分析概述
- 因子分析法通过研究变量间的相关系数矩阵,把这些变量间错综复杂的关系归结成少数几个综合因子,这一分析过程也称为降维。由于因子往往比主成分更易得到解释,从而有更广泛的应用。
- 举例:林登(Linden)根据他收集的来自139名运动员的比赛数据,对第二次世界大战以来奥林匹克十项全能比赛的得分作了因子分析研究。这十个全能项目为:100米跑( x 1 x_1 x1),跳远( x 2 x_2 x2),铅球( x 3 x_3 x3),跳高( x 4 x_4 x4),400米跑( x 5 x_5 x5),11米跨栏( x 6 x_6 x6),铁饼( x 7 x_7 x7),撑杆跳高( x 8 x_8 x8),标枪( x 9 x_9 x9),1500米跑( x 10 x_{10} x10)。经标准化后所作的因子分析表明,十项得分基本上可归结于他们的短跑速度、爆发性臂力、爆发性腿力和耐力这四个方面,每一方面都称为一个因子。十项得分与这四个因子之间的关系可以描述为如下的因子模型:
x i = μ i + a i 1 F 1 + a i 2 F 2 + a i 3 F 3 + a i 4 F 4 + ε i , i = 1 , 2 , ⋯ , 10 x_i=μ_i+a_{i1}F_1+a_{i2}F_2+a_{i3}F_3+a_{i4}F_4+ε_i, i=1,2,⋯,10 xi=μi+ai1F1+ai2F2+ai3F3+ai4F4+εi,i=1,2,⋯,10
其中- F 1 , F 2 , F 3 , F 4 F_1,F_2,F_3,F_4 F1,F2,F3,F4表示四个因子,出现在每个变量的表达式中,是不可观测的变量,称为公共因子(common factor)。
- a i j a_{ij} aij称为 x i x_i xi在因子 F j F_{j} Fj上的载荷(loading), A = ( a i j ) A = (a_{ij}) A=(aij)称为载荷矩阵。
- μ i \mu_i μi是 x i x_i xi的均值。
- ε i ε_i εi是 x i x_i xi不能被四个公共因子解释的部分,仅与变量 x i x_i xi有关,称之为特殊因子(specific factor),常假定 ε i ∼ N ( 0 , σ i 2 ) ε_i\sim N(0,σ_i^2 ) εi∼N(0,σi2), σ i 2 σ_i^2 σi2称为特殊方差。
- 因子分析的首要任务就是估计因子载荷 a i j a_{ij} aij和方差 σ i 2 σ_i^2 σi2 ,然后给因子 F j F_{j} Fj一个合理的解释,若难以进行合理的解释,则需要进一步作因子旋转,希望旋转后能发现比较合理的解释。
因子分析模型
数学模型
设有 p p p个原始变量 x i x_i xi,标准化后为 X i X_i Xi(一般都要标准化),它们可能相关,则可以建立因子分析模型如下:
X i = μ i + a i 1 F 1 + a i 2 F 2 + . . . + a i m F m + ε i , i = 1 , 2 , ⋯ , p , m ≤ p X_i=μ_i+a_{i1}F_1+a_{i2}F_2+...+a_{im}F_m+ε_i, i=1,2,⋯,p,m\le p Xi=μi+ai1F1+ai2F2+...+aimFm+εi,i=1,2,⋯,p,m≤p
或
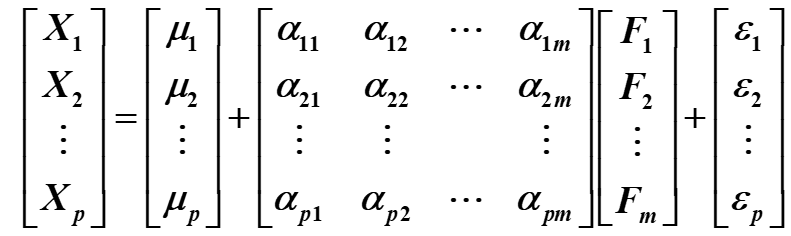
或
X − μ = Λ F + εX−μ=ΛF+εX − μ = Λ F + ε " role="presentation" style="position: relative;">
并且满足
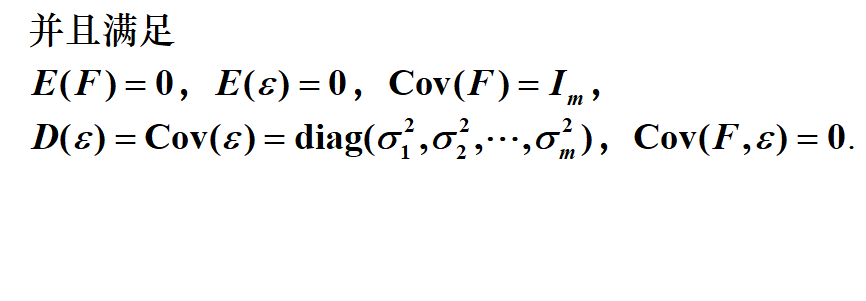
因子分析模型的性质
- X X X的协方差矩阵的分解
C o v ( X ) = Λ Λ T + d i a g ( σ 1 2 , σ 2 2 , . . . , σ 3 2 )
Cov(X)=ΛΛT+diag(σ12,σ22,...,σ32)C o v ( X ) = Λ Λ T + d i a g ( σ 1 2 , σ 2 2 , . . . , σ 3 2 ) " role="presentation" style="position: relative;">
X X X是经过标准化的,所以 C o v ( X i ) = 1 Cov(X_i)=1 Cov(Xi)=1- 载荷矩阵不是唯一的
设 T T T为一个p×p的正交矩阵,令
Λ ~ = Λ T , F ~ = T T F \tilde\varLambda=\varLambda T,\tilde F=T^TF Λ~=ΛT,F~=TTF
则(1)可以表达为
X − μ = Λ ~ F ~ + ε X-\mu=\tilde\varLambda \tilde F+\varepsilon X−μ=Λ~F~+ε
并且新的公共因子 F ~ \tilde F F~依旧满足条件。因子载荷矩阵的几个统计性质
- 因子载荷 a i j a_{ij} aij的统计意义
因子载荷 a i j a_{ij} aij是第 i i i个变量与第 j j j个公共因子的相关系数,即 a i j = r x i F j a_{ij}=r_{x_iF_j} aij=rxiFj
- 变量 X i X_i Xi共同度的统计意义
变量 X i X_i Xi的共同度是因子载荷矩阵的第 i i i行的元素的平方和,记为 h i 2 = ∑ j = 1 m a i j 2 h_i^2=\sum_{j=1}^ma_{ij}^2 hi2=∑j=1maij2,由(2)式得到
1 = ∑ j = 1 m a i j 2 + σ i 2 1=\sum_{j=1}^ma_{ij}^2+\sigma_i^2 1=∑j=1maij2+σi2
所有公共因子和特殊因子对变量 X i X_i Xi的贡献为1,如果共同都非常靠近1,则从原变量空间到公共因子空间的转化效果好。- 公共因子 F j F_j Fj方差贡献的统计意义
F j F_j Fj对所有的 X i X_i Xi的方差贡献和是因子载荷矩阵的第 j j j行的元素的平方和,记为 S j = ∑ i = 1 p a i j 2 S_j=\sum_{i=1}^p a_{ij}^2 Sj=∑i=1paij2,用以衡量 F j F_j Fj的相对重要性。
因子载荷矩阵的估计方法
主成分分析方法
样本相关系数矩阵 R = c o r r c o e f ( x ) = c o v ( X ) = c o r r c o e f ( X ) R=corrcoef(x)=cov(X)=corrcoef(X) R=corrcoef(x)=cov(X)=corrcoef(X), λ 1 ≥ λ 2 ≥ . . . ≥ λ p \lambda_1\ge\lambda_2\ge...\ge\lambda_p λ1≥λ2≥...≥λp为 R R R的特征值, η 1 , η 2 , . . . , η p \eta_1,\eta_2,...,\eta_p η1,η2,...,ηp为相应的标准正交化特征向量。
则因子载荷矩阵
Λ = [ λ 1 η 1 , λ 2 η 2 , . . . , λ p η p ] \varLambda=[\sqrt{\lambda_1}\eta_1,\sqrt{\lambda_2}\eta_2,...,\sqrt{\lambda_p}\eta_p] Λ=[λ1η1,λ2η2,...,λpηp]
特殊因子的方差
σ i 2 = 1 − ∑ j = 1 m a i j 2 \sigma_i^2=1-\sum_{j=1}^ma_{ij}^2 σi2=1−j=1∑maij2主因子法
记
R ∗ = Λ Λ T = R − d i a g ( σ 1 , . . . , σ m ) R^*=\varLambda\varLambda^T=R-diag(\sigma_1,...,\sigma_m) R∗=ΛΛT=R−diag(σ1,...,σm)
R ∗ R^* R∗为约相关系数矩阵,对角线上的元素是 h i 2 h_i^2 hi2。
特殊因子的方差一般是未知的,通过如下方法进行估计:- 取 h ^ i 2 = 1 \hat h_i^2=1 h^i2=1,这种情况下主因子解与主成分解等价。
- 取 h ^ i 2 = max j ≠ i ∣ r i j ∣ \hat h_i^2=\max_{j\not = i}|r_{ij}| h^i2=maxj=i∣rij∣
记
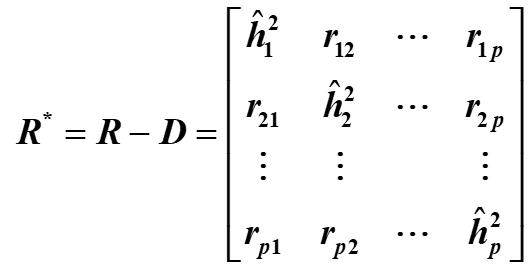
λ 1 ∗ ≥ λ 2 ∗ ≥ . . . ≥ λ p ∗ \lambda_1^*\ge\lambda_2^*\ge...\ge\lambda_p^* λ1∗≥λ2∗≥...≥λp∗为 R R R的特征值, η 1 ∗ , η 2 ∗ , . . . , η p ∗ \eta_1^*,\eta_2^*,...,\eta_p^* η1∗,η2∗,...,ηp∗为相应的标准正交化特征向量。
则因子载荷矩阵
Λ = [ λ 1 ∗ η 1 ∗ , λ 2 ∗ η 2 ∗ , . . . , λ p ∗ η p ∗ ] \varLambda=[\sqrt{\lambda_1^*}\eta_1^*,\sqrt{\lambda_2^*}\eta_2^*,...,\sqrt{\lambda_p^*}\eta_p^*] Λ=[λ1∗η1∗,λ2∗η2∗,...,λp∗ηp∗]最大似然估计法
Matlab工具箱求因子载荷矩阵使用的是最大似然估计法,命令是factoran。
因子旋转
- 得到因子模型后,其中的公共因子不一定能反映问题的实质特征,为了能更好地解释每一个公共因子的实际意义,且减少解释的主观性,可以通过因子旋转达到目的。
- 因子旋转分为正交旋转与斜交旋转,经过正交旋转而得到的新的公共因子仍然保持彼此独立的性质,而斜交旋转得到的公共因子是相关的(违背了最初的假定,因此可以看作传统因子分析的拓展),其实际意义更容易解释。
- 不论是正交旋转还是斜交旋转,都应当使新公共因子的载荷系数的绝对值尽可能接近0或1。
正交变换
- 我们主要介绍正交变换,有三种主要的正交旋转法:方差最大法、四次方最大法、等量最大法。
- 方差最大法:使因子载荷矩阵中每一列的因子载荷平方的方差最大,使每个因子上的载荷尽量拉开距离。
- 四次方最大法:使因子载荷矩阵中每一行的因子载荷平方的方差最大,使每个变量只在一个因子上有较高的载荷。
- 等量最大法:把方差最大法和四次方最大法结合起来,求它们的加权平均最大。
- 当公共因子数m>2,从m个因子中每次选两个旋转,做完m(m-1)/2次旋转就算完成了一次循环,然后就可以开始第二次循环,直到每个因子的含义都比较明确未知。
因子得分
因子得分的概念
- 前面用公共因子的线性组合来表示一组观测变量,如果要用这些因子做其它的研究,比如把得到的因子作为自变量来做回归分析、对样本进行分类或评价,就需要得到公共因子的值。
- 因子分析的数学模型
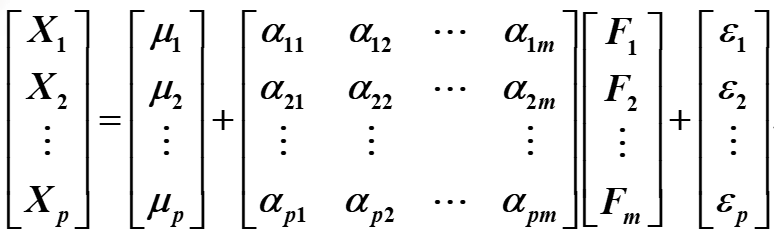
- 因子得分函数
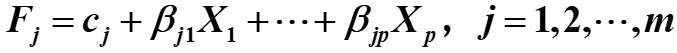
巴特莱特因子得分(加权最小二乘法)
F ^ = ( Λ T D − 1 Λ ) − 1 Λ T D − 1 ( X − μ ) \hat F=(\varLambda^TD^{-1}\varLambda)^{-1}\varLambda^TD^{-1}(X-\mu) F^=(ΛTD−1Λ)−1ΛTD−1(X−μ)
D = d i a g ( σ 1 2 , σ 2 2 , . . . , σ p 2 ) D=diag(\sigma_1^2,\sigma_2^2,...,\sigma_p^2) D=diag(σ12,σ22,...,σp2)回归方法
F ^ = X R − 1 Λ \hat F=XR^{-1}\varLambda F^=XR−1Λ
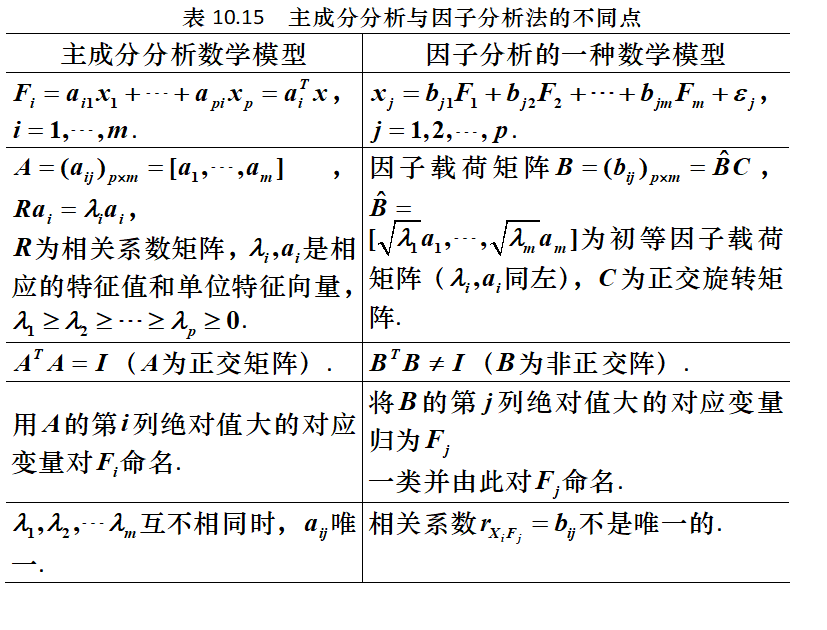
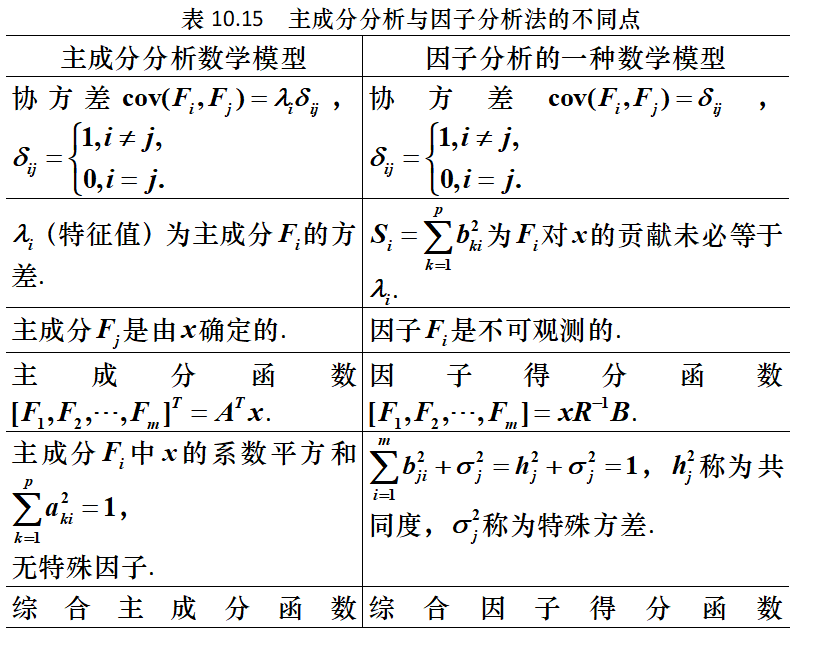
主成分分析和因子分析数学模型的比较
- 相同点

- 不同点
因子分析案例
我国上市公司盈利能力与资本结构的实证分析
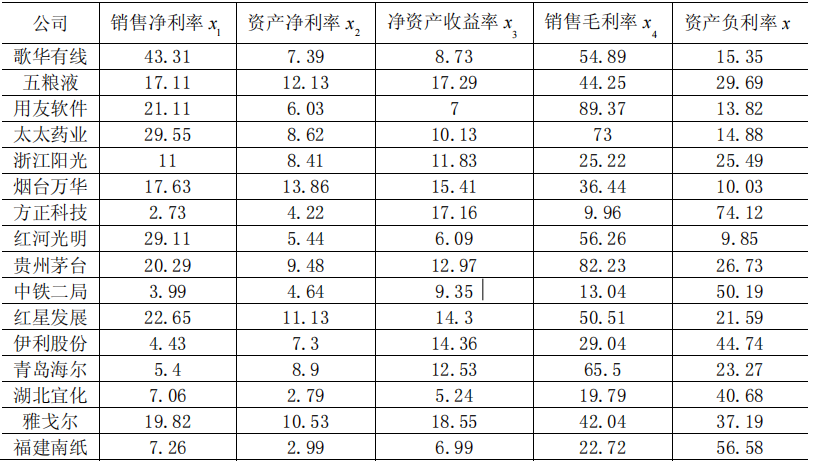
- 对原始数据进行标准化处理
- 计算相关系数矩阵 R = ( r i j ) 4 × 4 R=(r_{ij})_{4\times 4} R=(rij)4×4
- 计算初等载荷矩阵
- 选择2个主因子,并对提取的因子载荷矩阵进行旋转
贡献率数据 因子 贡献 贡献率 累计贡献率 1 1.7794 44.49 44.49 2 1.6673 41.68 86.17 旋转因子分析表 指标 主因子1 主因子2 销售净利率 0.893 0.0082 资产净利率 0.372 0.8854 净资产收益率 -0.2302 0.9386 销售毛利率 0.8892 0.0494 主因子1是销售利润银子,主因子2是资产收益因子。
- 计算因子得分,并进行综合得分
各个因子得分函数为
F 1 = 0.513 x ~ 1 + 0.1615 x ~ 2 − 0.1831 x ~ 3 + 0.5015 x ~ 4 F 2 = − 0.045 x ~ 1 + 0.5151 x ~ 2 + 0.581 x ~ 3 − 0.0199 x ~ 4 F_1=0.513\tilde x_1+0.1615\tilde x_2-0.1831\tilde x_3+0.5015\tilde x_4\\ F_2=-0.045\tilde x_1+0.5151\tilde x_2+0.581\tilde x_3-0.0199\tilde x_4 F1=0.513x~1+0.1615x~2−0.1831x~3+0.5015x~4F2=−0.045x~1+0.5151x~2+0.581x~3−0.0199x~4
利用综合因子得分公式
F = 44.49 F 1 + 41.68 F 2 86.17 F=\frac{44.49F_1+41.68F_2}{86.17} F=86.1744.49F1+41.68F2
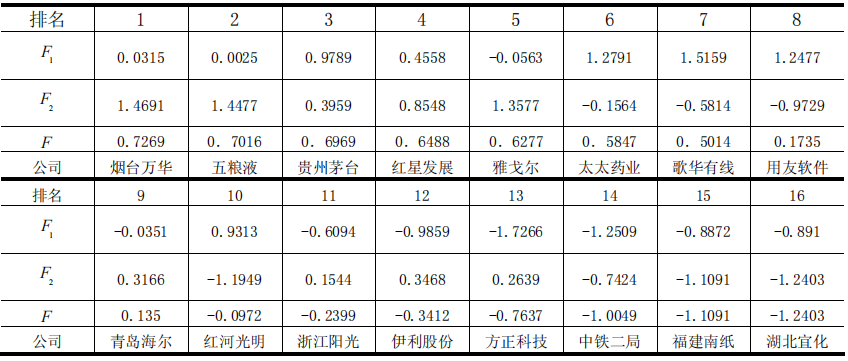
- 盈利能力F和资产负债率y之间的关系:
F = 0.829 − 0.0268 y F=0.829-0.0268y F=0.829−0.0268y
回归方程在显著性水平0.05的情况下,通过了显著性检验。clc,clear load ssgs.txt %把原始数据保存在纯文本文件ssgs.txt中 n=size(ssgs,1); %样本数 x=ssgs(:,1:4);y=ssgs(:,5);%提取自变量和因变量 X=zscore(x); %对x进行标准化 R=corrcoef(X);%求相关系数矩阵 [vec1,val,con1]=pcacov(R); %进行主成分分析的相关计算,vec1特征向量,val特征值,con1贡献率 f1=repmat(sign(sum(vec1)),size(vec1,1),1); vec2=vec1.*f1; %特征向量正负号转换 f2=repmat(sqrt(val)',size(vec2,1),1); a=f2.*vec2; %初等载荷矩阵,选取前两个因子,但是载荷没有接近±1,0,所以旋转因子 am=a(:,1:2);%提出前两列的载荷矩阵 [bm,t]=rotatefactors(am,'Method','varimax');%bm旋转后的载荷矩阵,t正交矩阵 bt=[bm,a(:,3:end)];%旋转后全部因子的载荷矩阵 con2=sum(bt.^2);%因子贡献是每列平方和 rate=con2/sum(con2);%因子贡献率 %注意旋转前和旋转后的贡献率是不一样的,但前两个贡献率之和一样 check=[con1,rate'*100]; coef=inv(R)*bm;%得分函数的系数 score=X*coef;%计算样本在两个因子上的得分 Tscore=(rate(1)*score(:,1)+rate(2)*score(:,2))/sum(rate(1:2));%计算综合得分 [STscore,ind]=sort(Tscore,'descend');%降序排序 display=[score(ind,:)';STscore';ind']; %显示排序结果 [d,dt,e,et,stats]=regress(Tscore,[ones(n,1),y]);%计算F与资产负债的方程,p值=0.0026,通过显著性检验- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
-
相关阅读:
jmeter下载地址
公元是什么意思,公历和农历
【2023保研】双非上岸东南网安
Cookie
OpenCV官方教程中文版 —— 傅里叶变换
终于有阿里p9架构师分享出困扰我多年的分布式系统开发实战文档
什么是单片机最小系统?
【压缩感知 SDA】A Deep Learning Approach to Structured Signal Recovery
卷积神经网络(CNN)
volatile详解和静态内部类详解
- 原文地址:https://blog.csdn.net/weixin_45775970/article/details/126317648
