【算法】顺序表力扣OJ

1.移除元素

题目链接

27. 移除元素 - 力扣（LeetCode）

题目描述

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

法一

思路：

循环遍历，挪动数组的数据到新空间。开辟一个新的数组，遍历原来的数组，将不等于val的元素放进新开辟的数组中，最后让新开辟的的数组覆盖原数组。这种方式是以空间换时间。

时间复杂度：O(N) 空间复杂度：O(N)

代码：

int removeElement(int* nums, int numsSize, int val){
    int k = 0;
    int i = 0;
    int* arr = (int*)malloc(numsSize*sizeof(int));
    for(i = 0; i < numsSize; i++)
    {
        if(nums[i]!=val)
        {
            arr[k++] = nums[i];//将不等于val的元素放进新开辟的数组
        }
    }
    for(i = 0; i < k; i++)//覆盖原数组
    {
        nums[i] = arr[i];
    }
    free(arr);
    arr = NULL;
    return k;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

法二

思路：

循环遍历，挪动覆盖数据。遍历这个数组，每当数组的元素等于val的值时，就将数组val后面的元素整体向前挪动一位，覆盖到val元素。

时间复杂度：O(N^2) 空间复杂度：O(1)

代码：

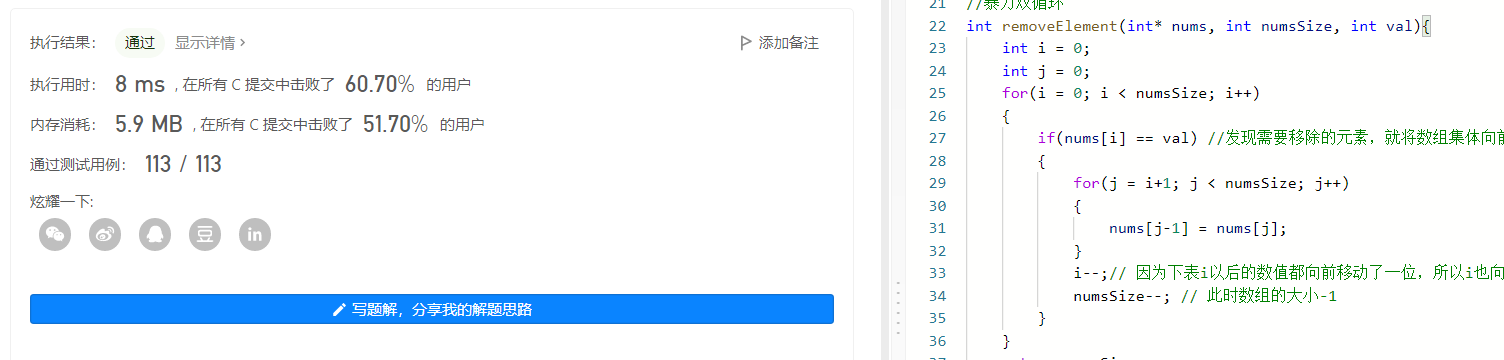
//暴力双循环
int removeElement(int* nums, int numsSize, int val){
    int i = 0;
    int j = 0;
    for(i = 0; i < numsSize; i++)
    {
        if(nums[i] == val) //发现需要移除的元素，就将数组集体向前移动一位
        {
            for(j = i+1; j < numsSize; j++)
            {
                nums[j-1] = nums[j];
            }
            i--;// 因为下表i以后的数值都向前移动了一位，所以i也向前移动一位
            numsSize--; // 此时数组的大小-1  
        }
    }
    return numsSize;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

法三

思路及算法：

遍历数组，挪动覆盖数据。这里我们用双指针(快慢指针)解法，定义两个指针，快指针fast，慢指针slow。快指针指向当前将要处理的元素， 慢指针指向下一个将要赋值的位置。如果快指针指向的元素不等于val，它一定是输出数组的一个元素，我们就将快指针指向的元素复制到慢指针位置，然后将快慢指针同时右移；如果快指针指向的元素等于 val，它不能在输出数组里，此时慢指针不动，快指针右移一位。

时间复杂度：O(N) 空间复杂度：O(1)

代码：

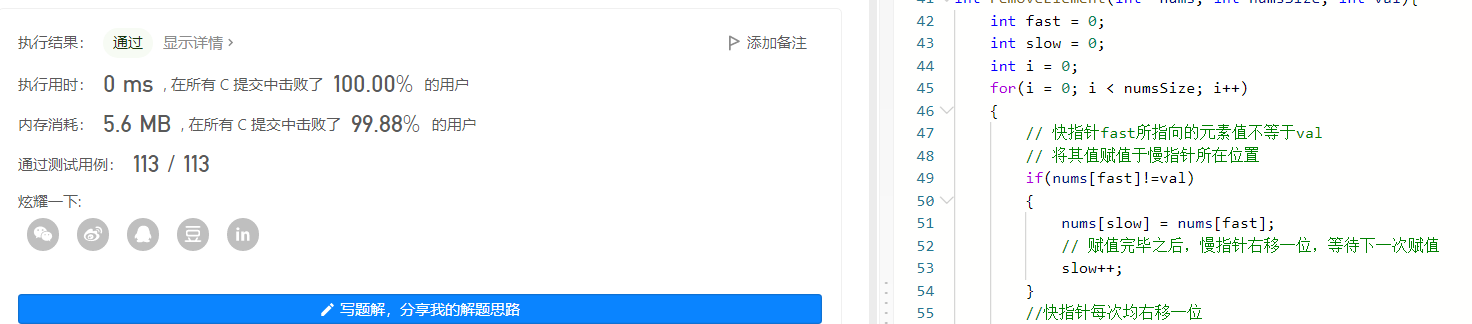
//双指针法
int removeElement(int* nums, int numsSize, int val) {
	int fast = 0;
	int slow = 0;
	int i = 0;
	for (i = 0; i < numsSize; i++)
	{
		// 快指针fast所指向的元素值不等于val
		// 将其值赋值于慢指针所在位置
		if (nums[fast] != val)
		{
			nums[slow] = nums[fast];
			// 赋值完毕之后，慢指针右移一位，等待下一次赋值
			slow++;
		}
		//快指针每次均右移一位
		fast++;
	}
	//慢指针的大小就是新的数组的大小
	return slow;
}

int removeElement(int* nums, int numsSize, int val)
{
	int slow = 0;
	for (int fast = 0; fast < numsSize; fast++)
	{
		if (nums[fast] != val)
		{
			nums[slow] = nums[fast];
			slow++;
		}
		fast++;
	}
	return slow;
}

int removeElement(int* nums, int numsSize, int val)
{
	int slow = 0;
    int fast = 0;
	while(fast < numsSize)
    {
        if(nums[fast] != val)
        {
            nums[slow++] = nums[fast++];
        }
        else
        {
            fast++;
        }
    }
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

法三双指针优化

思路：

如果要移除的元素恰好在数组的开头，例如序列 [1,2,3,4,5]，当 val 为 1 时，我们需要把每一个元素都左移一位。注意到题目中说：「元素的顺序可以改变」。实际上我们可以直接将最后一个元素 55 移动到序列开头，取代元素 11，得到序列 [5,2,3,4]同样满足题目要求。这个优化在序列中 val 元素的数量较少时非常有效。

实现方面，我们依然使用双指针，两个指针初始时分别位于数组的首尾，向中间移动遍历该序列。

算法：

如果左指针 left 指向的元素等于val，此时将右指针 right 指向的元素复制到左指针 left 的位置，然后右指针 right 左移一位。如果赋值过来的元素恰好也等于val，可以继续把右指针 right 指向的元素的值赋值过来（左指针 left 指向的等于 val 的元素的位置继续被覆盖），直到左指针指向的元素的值不等于 val 为止。当左指针 left 和右指针 right 重合的时候，左右指针遍历完数组中所有的元素。

这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。与方法一不同的是，方法二避免了需要保留的元素的重复赋值操作。所以我们只需要遍历该数组至多一次。

代码：

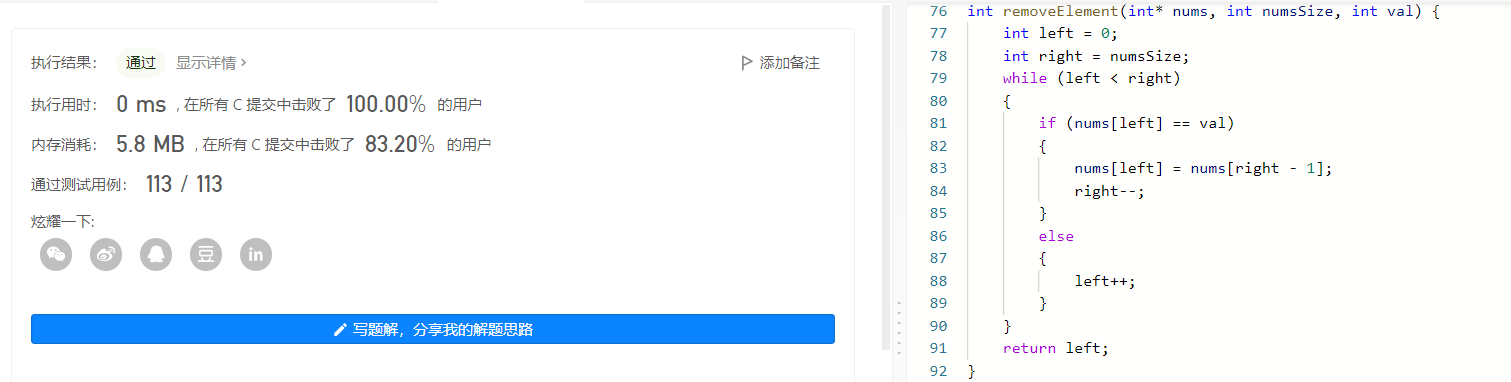
int removeElement(int* nums, int numsSize, int val) {
    int left = 0;
    int right = numsSize;
    while (left < right) 
    {
        if (nums[left] == val)
        {
            nums[left] = nums[right - 1];
            right--;
        }
        else
        {
            left++;
        }
    }
    return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.删除有效数组中的重复项

题目链接

26. 删除有序数组中的重复项 - 力扣（LeetCode）

题目描述

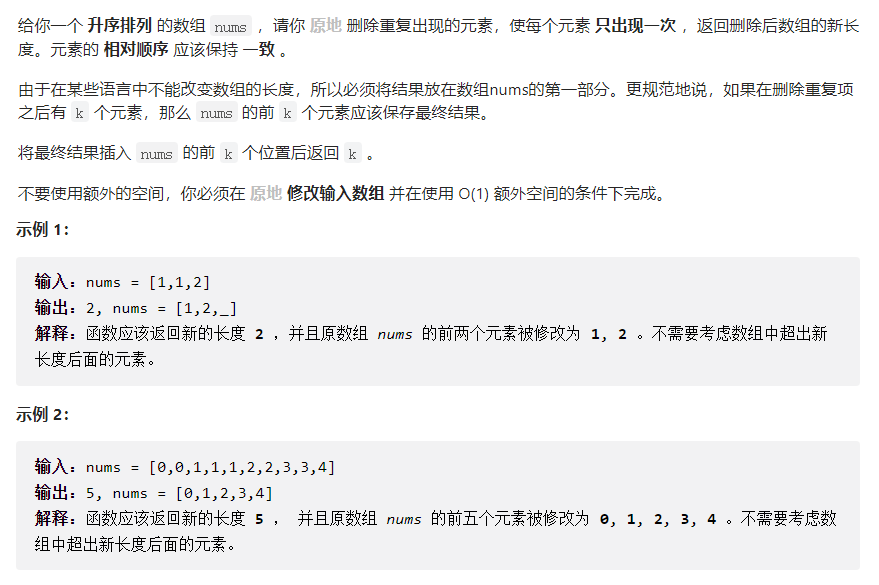
给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。将最终结果插入 nums 的前 k 个位置后返回 k 。不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

法一

思路：这道题与上面那道题很相似，我们仍然使用双指针，快指针指向当前将要处理的元素， 慢指针指向下一个将要赋值的位置。

遍历整个数组，循环条件为 fast＜当前数组长度。每次循环 fast 都会做判断，判断 fast 当前数字是否等于 fast 后面那个数，把不重复的数赋值给slow，然后 slow，fast 全部自增，如果当前 fast 的数等于 fast 后面的数，（因为数组是有序的所以只用判断fast后面的数，而不是与 slow 判断）就只让 fast 自增，直到 fast 找到不等于 fast 后面的数，再次让fast的数赋值 slow，当 fast 的数超出数组长度，返回slow 当前数字，就是不重复的数组长度。

时间复杂度：O(N) 空间复杂度：O(1)

代码：

//双指针法
int removeDuplicates(int* nums, int numsSize){
    int i = 0;
    int fast = 1;
    int slow = 1;
    while(fast < numsSize)
    {
        if(nums[fast] != nums[fast-1])
        {
            nums[slow] = nums[fast];
            slow++;
        }
        fast++;
    }
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

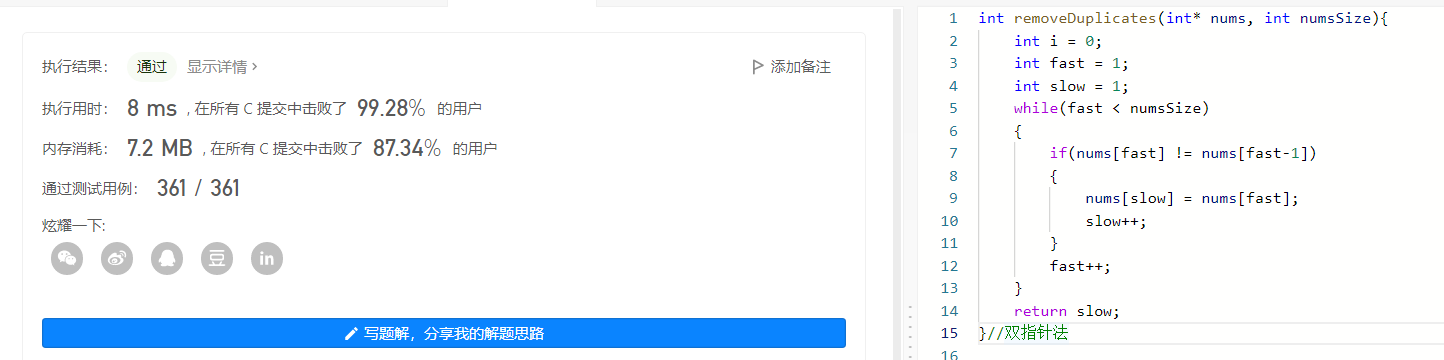
法二

思路：

这也是双指针，不过是另一种表现形式。快指针指向当前将要处理的元素， 慢指针指向下一个将要赋值的位置。

如果快指针指向的元素不等于慢指针指向的元素，我们就将快指针指向的元素复制到慢指针位置，然后将快慢指针同时右移；如果快指针指向的元素等于慢指针指向的元素，它不能在输出数组里，此时慢指针不动，快指针右移一位。

时间复杂度：O(N) 空间复杂度：O(1)

代码：

//双指针法
int removeDuplicates(int* nums, int numsSize){
    int i = 0;
    int fast = 0;
    int slow = 0;
    while(fast < numsSize)
    {
        if(nums[fast] != nums[slow])
        {
            nums[++slow] = nums[fast++];
        }
        else
        {
            fast++;
        }
    }
    return slow+1;
    //由于slow是前置++，所以返回值需要+1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

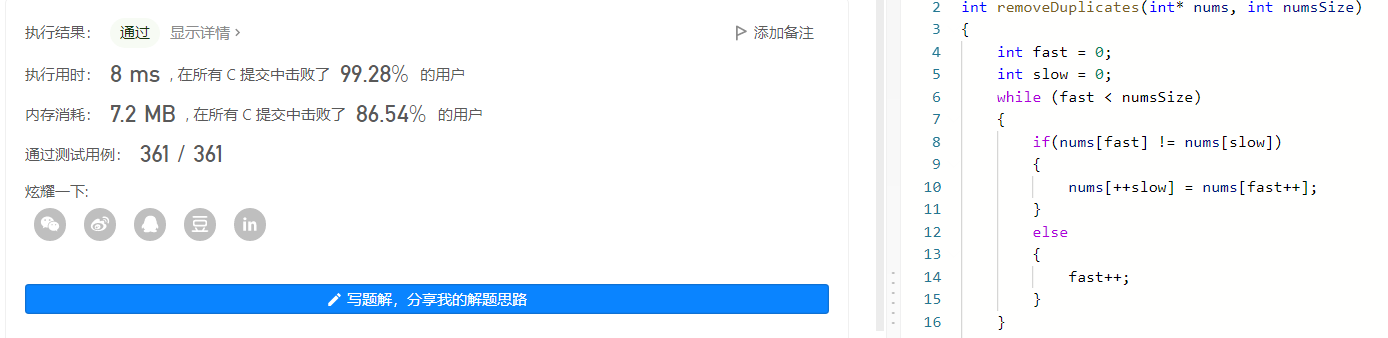
法三

思路：

这是单指针，其实本质上也是双指针。index指针就相当于慢指针，下标i就相当于快指针，其他的都差不多，这里就不赘述了。

时间复杂度：O(N) 空间复杂度：O(1)

代码：

//单指针法
int removeDuplicates(int* nums, int numsSize){
    int index=0;
       //index指针指向替换位，i遍历，替换前后不同元素
        for(int i=1;i<numsSize;i++)
        {
            if(nums[i-1]!=nums[i]
            {
                nums[++index]=nums[i];
            }
        }
        return index+1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

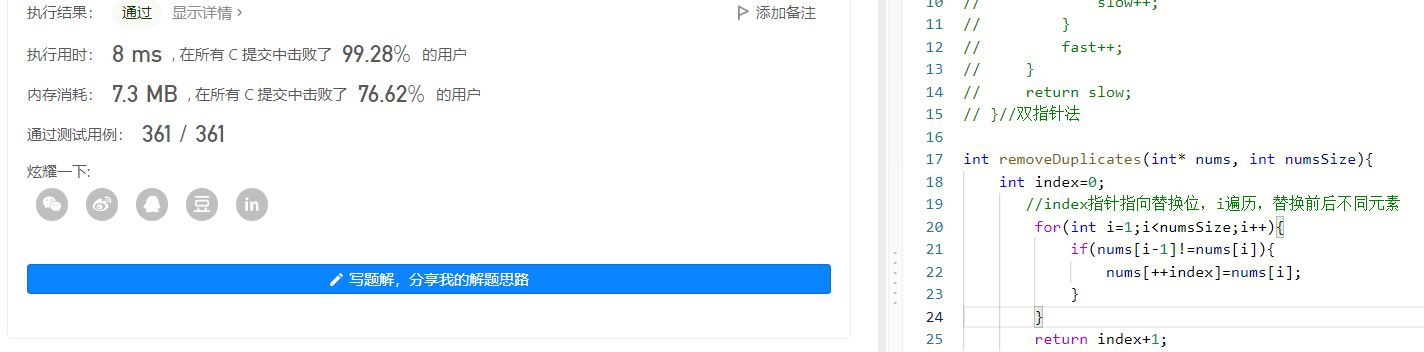
3.合并两个有序数组

题目链接

88. 合并两个有序数组 - 力扣（LeetCode）

题目描述

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你合并nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

法一

思路：

最直观的方法是先将数组 nums2 的元素覆盖掉数组 nums1 的尾部为0的数字，然后直接对整个数组进行排序。

时间复杂度：O((m+n)*log(m+n)) 空间复杂度：O(log(m+n))

代码：

int cmp_by_int(const void* a, cosnt void* b) {
    return *(int*)a - *(int*)b;
}

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    for (int i = 0; i < n; ++i)
    {
        nums1[m + i] = nums2[i];
    }
    qsort(nums1, nums1Size, sizeof(int), cmp_by_int);
}
1
2
3
4
5
6
7
8
9
10
11

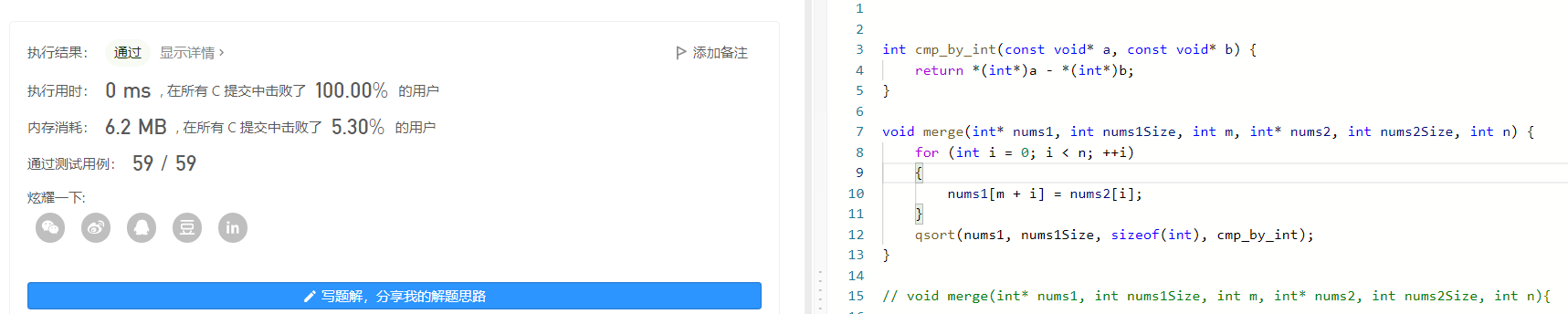
法二

思路：

从后向前数组遍历，因为 nums1 的空间都集中在后面，所以从后向前处理排序的数据会更好，节省空间，一边遍历一边将值填充 ，进去设置指针 str1 和 str2 分别指向 nums1 和 nums2 的非0数字尾部，从尾部值开始比较遍历，同时设置指针 end 指向 nums1 的最末尾，每次遍历比较值大小之后，则进行填充当 str1<0或str2<0 时遍历结束，此时如果 nums2 中还有数据未完全拷贝到nums1，将其直接拷贝到 nums1 的前面，如果 nums2 中数据全都拷贝到nums1，不用管它，，最后得到结果数组。

时间复杂度：O(m+n) 空间复杂度：O(m+n)

代码：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){

    int src1 = m - 1;  //指向数组1最后一个非0数据
    int src2 = n - 1;  //指向数组2末尾
    int end = m+n-1;   //指向数组1末尾
    while(src1 >=0 && src2 >= 0)  //当其中一个数组遍历完成后循环结束
    {
        if(nums1[src1] > nums2[src2])  
        {
            nums1[end--] = nums1[src1--];
        }
        else
        {
            nums1[end--] = nums2[src2--];
        }
    }
    //src2结束，nums2的数组都拷贝过去了，那么不用处理
    //src1结束，nums1的数组都拷贝过去了，那么需要再把nums2剩下的数据拷贝过去
    if(src2 >= 0) 
    {
        while(src2 >= 0)
        {
            nums1[end--] = nums2[src2--];
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26