01背包

原理

模板

最全 LeetCode 背包问题目录（持续更新）

0-1背包

求存包最大数量

for(int i=0 ; i<stones.length ; i++){
     for(int j=mid ; j>=stones[i] ; j--){
         dp[j]= dp[j-stones[i]]+stones[i];
     }
 }
1
2
3
4
5

求存包最大容量

for(int i=0 ; i<stones.length ; i++){
     for(int j=mid ; j>=stones[i] ; j--){
         dp[j]=Math.max(dp[j] , dp[j-stones[i]]+stones[i]);
     }
 }
1
2
3
4
5

求存包的产生的最大价值

for(int i=0 ; i<stones.length ; i++){
     for(int j=mid ; j>=stones[i] ; j--){
         dp[j]=Math.max(dp[j] , dp[j-stones[i]]+values[i]);
     }
 }
1
2
3
4
5

完全背包

币的数量无限

币的数量有限

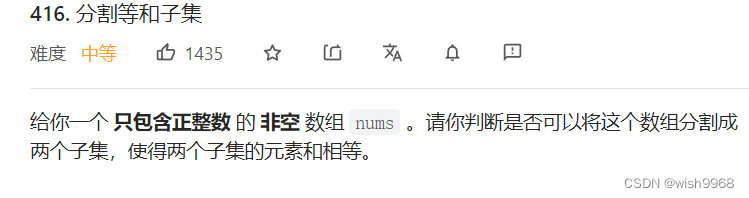
416分割等和子集

关键字：组合、01背包

题解
将分割问题转化为 01背包问题：放与不放

从n件物品中，拿出物品 放入总大小为target的包中，使得价值为target

int[] dp=new int[target+1];
dp[i]代表着 和为i的组合总数
1
2

求解dp[i]值为i的组合数

for(int i=0 ; i<nums.length ; i++){
    for(int j=target ; j>=nums[i] ; j--){
        dp[j]+=dp[j-nums[i]];
    }
}
1
2
3
4
5

可以优化加快时间

for(int i=0 ; i<nums.length ; i++){
    for(int j=target ; j>=nums[i] ; j--){
        dp[j]+=dp[j-nums[i]];
        if(dp[target]!=0) break;
    }
    if(dp[target]!=0) break;
}
1
2
3
4
5
6
7

494目标和

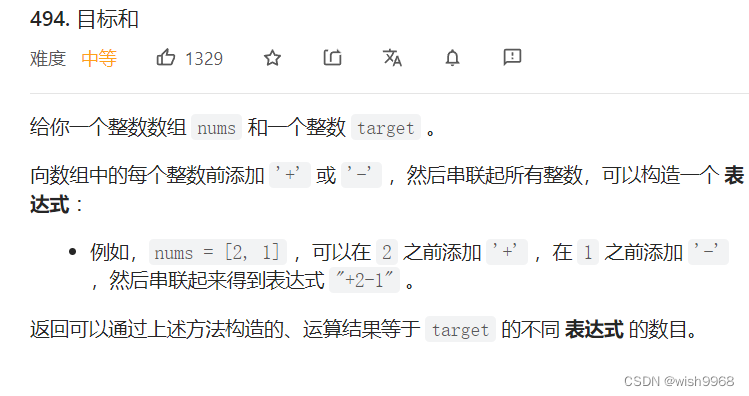
回溯法：

一增一减 回溯寻找到合适的值 count++  但是时间复杂度大
private void dfs(int[] nums,int target,int index){
    if(index==nums.length){
        if(res==target) count++;
        return;
    }
        //一个前置+号 
        res+=nums[index];
        dfs(nums,target,index+1);
        res-=nums[index];
        //一个前置-号 
        res-=nums[index];
        dfs(nums,target,index+1);
        res+=nums[index];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

动态规划解法
思路：

nums之和拆为s1和s2，总和为sum
那么s1+s2=sum;
且如果能与target匹配
必有s1-s2=target;（或者反过来 这不重要）

二者结合s1-s2+s1+s2=2*s1=sum+target;
s1=(sum+target)/2;
1
2
3
4
5
6
7

题意转化为背包问题：数组中值之和等于target

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum=0;
        for(int n : nums){
            sum+=n;
        }
        if((sum+target)%2!=0) return 0;
        int tar=(sum+target)/2;
        //求数组中  组合数 和为tar的数目
        int[] dp=new int[Math.abs(tar)+1];
        dp[0]=1;//和值为0时必有一种组合 即空值
        for(int i=0 ; i<nums.length ; i++){
            for(int j=tar ; j>=nums[i] ; j--){
                dp[j]+=dp[j-nums[i]];
            }
        }
        return dp[Math.abs(tar)];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

474——较难

这题稍有难理解
在于双 01 背包

//双 01背包
int[][] dp=new int[m+1][n+1];
for(String s : strs){
    int zeros=0,one=0;
    for(char ch : s.toCharArray()){
        if(ch=='0') zeros++;
        else one++;
    }
    //获取了当前字符01情况   在之前的基础上 0 1 数目小于 m 和 n的情况
    for(int i=m ; i>=zeros ; i--){
        for(int j=n ;j>=one ; j--){
            dp[i][j]=Math.max(dp[i][j] , dp[i-zeros][j-one]+1);
        }
    }
}
return dp[m][n];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

1049

题意：石头之间互相碰撞抵消

将其转换为  一个背包最多存储mid=sum/2的问题
stones中能存储背包的值v，说明如果再加一块石头i就会超出背包容量，
如果v小于背包容量，说明第二个背包也能存放v的容量，因为v小于mid值
说明两个背包可以抵消  即最后剩余的就是新石头
1
2
3
4

int sum=0;
 for(int n :stones) sum+=n;
 int mid=sum/2;

 int[] dp=new int[mid+1];
 //dp[0]=0;//背包容量为0  时  能存放的值也为0

 for(int i=0 ; i<stones.length ; i++){
     for(int j=mid ; j>=stones[i] ; j--){
         dp[j]=Math.max(dp[j] , dp[j-stones[i]]+stones[i]);
     }
 }

 return sum-dp[mid]*2;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

879

双背包问题 较难
集团员工人数上限 n，以及工作产生的利润下限 minProfit。

1230

完全背包

322

币的数量无限（先遍历目标值，再从头开始遍历数组），求组合为target的最少数目。

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp=new int[amount+1];
        Arrays.fill(dp, amount+1);
        dp[0]=0;
        for(int j=1 ; j<=amount ; j++){
            for(int i=0 ; i<coins.length ; i++){
                if(j>=coins[i]) dp[j]=Math.min(dp[j] , dp[j-coins[i]]+1);
            }
        }
        return dp[amount]==amount+1 ? -1 : dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

377

币的数量无限（先遍历目标值，再从头开始遍历数组），，组合数为target的总组合数目

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp=new int[target+1];
        //组合数
        dp[0]=1;

        for(int i=1 ; i<=target ; i++){
            for(int j=0 ; j<nums.length ; j++){
                if(i>=nums[j]) dp[i]+=dp[i-nums[j]];
            }
        }

        return dp[target];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

518

币的数目有限（先遍历钱包，再以钱包值为起点遍历目标值），求组合数目为target的情况

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp=new int[amount+1];
        dp[0]=1;
        for(int i=0 ; i<coins.length ; i++){
            for(int j=coins[i] ; j<=amount; j++){
                dp[j]+=dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

279

币无限 求组合为target的完全背包问题

class Solution {
    public int numSquares(int n) {
        int res=(int)Math.sqrt(n);
        if(res*res==n) return 1;

        //转化为完全背包
        //目标值为n   币的数量无限 存放到容量为n的包中  求最小装满值
        int[] dp=new int[n+1];
        Arrays.fill(dp , n+1);
        dp[0]=0;
        int mid=(int)n/2;
        int[] coin=new int[mid];
        for(int i=0 ; i<mid ; i++) coin[i]=(i+1)*(i+1);
        //如何构造数组呢
        for(int i=1 ; i<=n ; i++){
            for(int j=0 ; j<coin.length ; j++){
                if(i >= coin[j]) dp[i]=Math.min(dp[i] , dp[i-coin[j]]+1);
            }
        }

        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

1449

暂时不能理解

后续搞懂并查集