DP-Laplace Mechanism

差分隐私概念回顾

定义

• 需要注意的是，根据上述定义，当delta=0时，我们通常直接说机制M是满足ε-DP的。
• 一个形象化的展示就是**将相邻数据集的查询结果概率化，**使得两个查询的概率分布比较相近。通过这种方式，我们来保护数据隐私同时使得对数据的查询结果尽量可靠。
  

Laplace分布

• Laplace分布是统计学中的概念**，是一种连续的概率分布**。如果随机变量的概率密度函数分布为
  
• 那么它就是拉普拉斯分布。其中，μ （一般取值为0）是位置参数，b > 0 是尺度参数。画出来就是长这样：
• 使用python- matplotlib来绘制概率分布图：
  

import matplotlib.pyplot as plt
import numpy as np
def laplace_function(x, lambda_):
    return (1/(2*lambda_)) * np.e**(-1*(np.abs(x)/lambda_))
x = np.linspace(-5,5,10000)
y1 = [laplace_function(x_,1) for x_ in x]
y2 = [laplace_function(x_,2) for x_ in x]
y3 = [laplace_function(x_,0.5) for x_ in x]

plt.plot(x, y1, color='r', label="lambda:1")
plt.plot(x, y2, color='g', label="lambda:2")
plt.plot(x, y3, color='b', label="lambda:0.5")

plt.title("Laplace distribution")
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

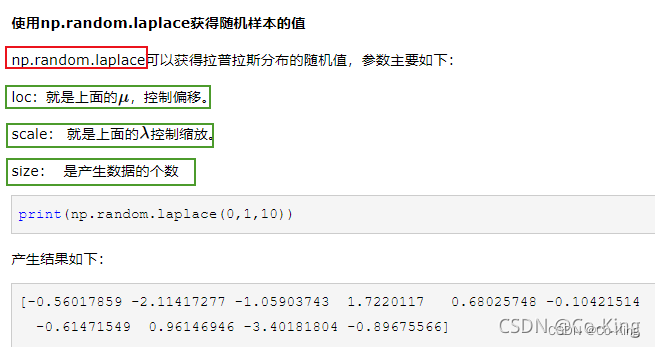
Laplace的应用

• 我们之前提到过，保护数据隐私的方法就是将原有的单一查询结果概率化。
• Laplace噪声就给我们提供了一个很好的概率化的方法。
• 举例：假如查询为“查询数据集中年龄小于20的人数”，并且查询结果为“50”，在传统模式下，输出就是50；**在差分隐私模式下，**会以比较大概率输出50左右的结果，也会以比较小的概率输出和50差别比较大的结果。但是，我们需要保证输出的期望为50（保证数据有效性）。
• **那么这个概率怎么用Laplace分布来呢？**我们可以直接在输出结果50上加均值为0的噪声。直观上来说，我们通过Laplace将查询结果概率化了。**那么是否Laplace噪声就满足差分隐私了呢？**我们慢慢道来。

Laplace噪声与DP

• 如何利用Laplace噪声产生符合DP的机制就成了我们主要研究的问题。
• 我们依然想一下DP的设计目标：“有你和没有你查询结果相差不大”。那么现在问题就来了，这个“有你”和“没有你”在真实情况下相差多少呢？

研究这个问题是因为我们不限定用户对数据集做出什么样的查询，直观上来说，如果查询的是人数，那么“有你”和“没有你”相差不大（只会相差1），只需要加一个小一点的噪声即可造成两个结果的混淆；那如果我们查询的是人的工资呢，加一个很小的噪声显然是无法满足应用需求的（因为数据相差太大，稍微对数据的改变依然可以看出数据差别很大）。由此可见，如何设计DP机制是和查询紧密相关的。所以我们需要对查询有一个简单的了解：

也因此，科学家们提出了**“敏感度”**的概念，我们先来看一下定义（f 就是我们的查询）：

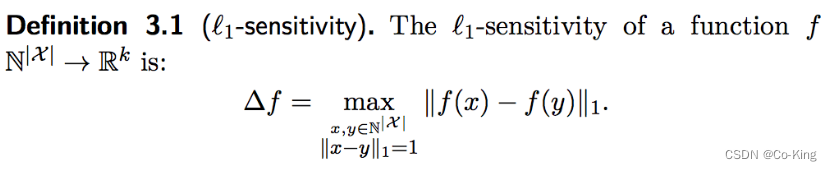
由于数据集中少一条记录就会对数据查询f的结果结果造成一定的影响，我们自然想知道，这个影响最大是多少呢？也就是上述定义中给出的敏感度的值Δf了。

有了Δf 之后，我们自然想：Δf 越大，噪声应该越大，Δf 越小，噪声应该越小。这就给我们设计接下来的机制给了一定的启发。

差分隐私机制

• 这里的Lap(Δf/ε) 即表示我们上面提到的拉普拉斯噪声中μ=0，b=Δf/ε.
• 同时上面的k表示的实际上是查询的维度。ε是人为定义的参数。
  
  上面这个简单的Laplace机制就满足ε-DP。 证明过程如下
  

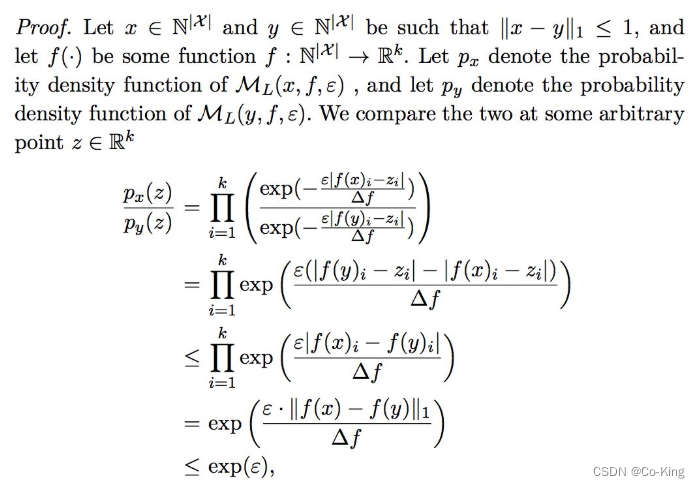
Laplace机制应用

案例一：Counting Queries（统计查询）
一般来说统计查询形如这样：“How many elements in the dataset satisfy property P”。即查询数据集中有多少条记录满足给定的条件。根据敏感度的定义，Counting Queries中敏感度为1。所以直接在查询结果上加Lap(0, 1/ε) 的噪声即可。

案例二：案例二：Histogram Queries（直方图查询）
在直方图查询中，首先作出数据的直方图，每一个直方图中的数据表示当前块（cell）中有多少记录。直方图查询即查询每一个cell中有多少记录。由于每个cell是独立的，改变数据集中一条记录只会影响到一个cell，因此敏感度为1。在这个模式下，和Counting Queries一样，只需要加上 Lap(0, 1/ε) 的噪声。