-
知识表示学习(二):TransH
一.摘要
我们处理将由实体和关系组成的大规模知识图谱嵌入到连续向量空间中。 TransE 是最近提出的一种很有前途的方法,它非常有效,同时实现了最先进的预测性能。我们讨论了嵌入中应该考虑的一些关系映射属性,例如自反、一对多、多对一和多对多。我们注意到 TransE 在处理这些属性方面做得不好。一些复杂的模型能够保留这些映射属性,但会牺牲过程中的效率。为了在模型容量和效率之间做出良好的权衡,在本文中,我们提出了 TransH,它将关系建模为超平面以及对其进行平移操作。这样,我们就可以很好地保留上述关系的映射属性,与TransE的模型复杂度几乎相同。另外,作为一个实际的知识图谱往往还远远没有完成,如何在训练中构造负样本来减少假负标签是非常重要的。利用关系的一对多/多对一映射属性,我们提出了一个简单的技巧来减少假阴性标记的可能性。我们在 WordNet 和 Freebase 等基准数据集上对链接预测、三元组分类和事实提取进行了广泛的实验。实验表明,与 TransE 相比,TransH 在预测准确性方面具有显着改进,并且具有可比的扩展能力。
二.背景介绍
Freebase 、WordNet 和 GeneOntology 等知识图谱已经成为支持许多 AI 相关应用程序的非常重要的资源,例如网络/移动搜索、问答等。 知识图谱是由作为节点的实体和作为不同类型边的关系组成的多关系图。 边的实例是事实的三元组(头实体、关系、尾实体)(表示为 (h, r, t))。在过去的十年中,构建大规模知识图谱取得了巨大成就,但支持计算的通用范式仍不清楚。 两个主要困难是:(1)知识图谱是一个符号和逻辑系统,而应用程序通常涉及连续空间中的数值计算; (2) 很难在图上聚合全局知识。传统的形式逻辑推理方法在处理真正的大规模知识图谱上的远程推理时既不易于处理也不鲁棒。 最近有人提出了一种新的方法来处理这个问题,它试图将知识图嵌入到一个连续的向量空间中,同时保留原始图的某些属性。例如,每个实体 h(或 t)表示为向量空间中的一个点 h(或 t),而每个关系 r 被建模为空间中的一个操作,该操作由一个向量 r 表征,例如平移、投影 等。通过最小化涉及所有实体和关系的全局损失函数来获得实体和关系的表示。 结果,即使是单个实体/关系的嵌入表示也会对来自整个知识图谱的全局信息进行编码。 然后嵌入表示可用于服务于各种应用程序。 一个简单的方法是在知识图中完成缺失的边。 对于任何候选三元组 (h, r, t),我们可以简单地通过检查表示 h 和 t 在以 r 为特征的操作下的兼容性来确认正确性。
通常,知识图嵌入将一个实体表示为一个 k 维向量 h(或 t),并定义一个评分函数 fr(h, t) 来衡量嵌入空间中三元组 (h, r, t) 的合理性。 得分函数意味着对表征关系 r 的实体对的变换 r。 对于不同的评分函数,隐含的变换在简单差异、平移、仿射、一般线性、 双线性和非线性变换。 因此,模型的复杂性(就参数数量而言)差异很大。
在以前的方法中,TransE是一种很有前途的方法,因为它简单高效,同时实现了最先进的预测性能。 然而,我们发现 TransE 在处理具有自反/一对多/多对一/多对多映射属性的关系时存在缺陷。
以前很少有工作讨论这些映射属性在嵌入中的作用。 一些具有更多自由参数的高级模型能够保留这些映射属性,但是模型复杂度和运行时间相应显着增加。 此外,高级模型的整体预测性能甚至比 TransE 还要差。 这促使我们提出一种方法,在模型复杂性和效率之间进行良好的权衡,以便在继承效率的同时克服 TransE 的缺陷。
在本文中,我们首先分析 TransE 在自反/一对多/多对一/多对多关系上的问题。 因此,我们提出了一种称为超平面平移(TransH)的方法,它将关系解释为超平面上的平移操作。 在 TransH 中,每个关系由两个向量表征,超平面的范数向量 (wr) 和超平面上的平移向量 (dr)。对于一个正确三元组 (h, r, t),它在世俗事实方面是正确的,h 和 t 在超平面上的投影预计通过平移向量 dr 连接,误差很小。 这种简单的方法克服了 TransE 在处理自反/一对多/多对一/多对多关系方面的缺陷,同时保持模型复杂度与 TransE 几乎相同。 关于模型训练,我们指出仔细构建负标签在知识嵌入中很重要。 通过依次利用关系的映射属性,我们提出了一个简单的技巧来减少假阴性标记的机会。 我们在 WordNet 和 Freebase 等基准数据集上对链接预测、三元组分类和事实提取任务进行了广泛的实验,在预测准确性的不同指标上显示出令人印象深刻的改进。 我们还表明 TransH 的运行时间与 TransE 相当。
三.在超平面上的变换(TransH)
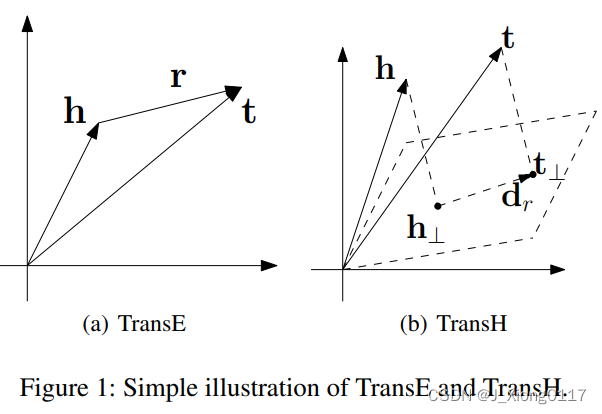
为了克服 TransE 在建模自反/一对多/多对一/多对多关系中的问题,我们提出了一个模型,该模型使实体能够在涉及不同关系时具有分布式表示。如下图所示,对于关系 r,我们将关系特定的平移向量 dr 定位在关系特定的超平面 wr(法线向量)中,而不是实体嵌入的同一空间中。 具体来说,对于三元组 (h, r, t),嵌入 h 和 t 首先投影到超平面 wr。 投影分别表示为 h⊥ 和 t⊥。 如果 (h, r, t) 是黄金三元组,我们期望 h⊥ 和 t⊥ 可以通过超平面上的平移向量 dr 以低误差连接。 因此,我们定义了一个评分函数 ||h⊥ + dr − t⊥k||2 来衡量三元组不正确的合理性。
通过限制||wr||2 = 1,很容易得到:
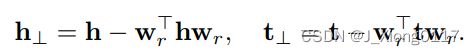
评分函数如下:
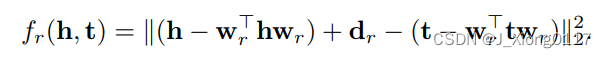
黄金三元组的分数预计会较低,而不正确的三元组的分数会更高,我们将此模型命名为 TransH。模型参数是所有实体的嵌入以及所有关系的超平面和平移向量。
在 TransH 中,通过引入投影到特定关系超平面的机制,它可以在不同的关系/三元组中实现实体的不同角色。训练
为了鼓励区分黄金(正确)三元组和不正确的三元组,我们使用以下基于边际的排名损失:
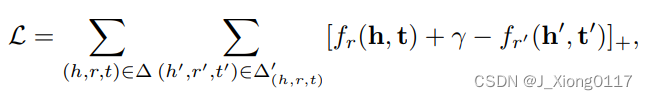
当我们最小化损失 L 时,考虑以下约束:

其中约束 (2) 保证平移向量 dr 在超平面中。 我们没有直接使用约束优化损失函数,而是通过软约束将其转换为以下无约束损失:
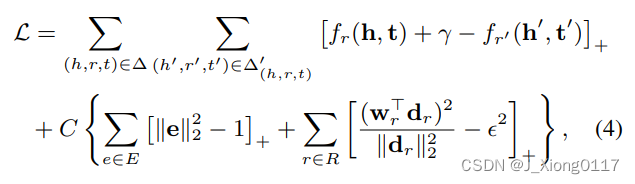
我们采用随机梯度下降(SGD)来最小化上述损失函数。 黄金(正确)三元组(知识图谱中的三元组)随机遍历多次。 当访问一个黄金(正确)三元组时,会随机构建一个负三元组, 在小批量之后,计算梯度并更新模型参数。
减少假阴性标签
训练涉及为黄金三元组构建负三元组。 以前的方法只是通过随机破坏黄金三元组来获得负三元组。 例如,在 TransE 中,对于一个黄金三元组 (h, r, t),通过从 E 中随机抽样一对实体 (h’, t’) 得到一个负三元组 (h’, r, t’)。然而 ,由于真正的知识图谱往往还远未完成,这种随机抽样的方式可能会在训练中引入许多假阴性标签。
我们对 TransH 采用不同的方法。 基本上,我们在破坏三元组时设置不同的替换头部或尾部实体的概率,这取决于关系的映射属性,即一对多、多对一或多对多。 如果关系是一对多的,我们倾向于给替换头部实体更多的机会,如果关系是多对一的,我们倾向于给替换尾部实体更多的机会。这样就减少了产生假阴性标签的机会。 具体来说,在关系 r 的所有三元组中,我们首先得到以下两个统计数据: (1) 每个头部实体的平均尾部实体数,记为 tph; (2) 每个尾部实体的平均头部实体数,记为 hpt。 然后我们定义一个带有参数 tph/(tph+hpt) 的伯努利分布进行采样:给定关系 r 的黄金三元组 (h, r, t),我们以 tph/(tph+hpt) 的概率破坏三元组,通过替换 头部,并且以概率 hpt/(tph+hpt) 我们通过替换尾部来破坏三元组。四.总结
在本文中,我们介绍了 TransH,这是一种将知识图嵌入连续向量空间的新模型。 TransH在继承其效率的同时克服了TransE关于自反/一对多/多对一/多对多关系的缺陷。 对链接预测、三元组分类和关系事实提取任务的大量实验表明,TransH 为 TransE 带来了有希望的改进。 本文提出的减少假阴性标签的技巧也被证明是有效的。
由于TransE模型只能处理一对一的关系,不适合自反/一对多/多对一/多对多关系,例如,有两个知识,(skytree, location, tokyo)和(gundam, location, tokyo),经过训练,“sky tree”实体向量将非常接近“gundam”实体向量,但实际上它们没有这样的相似性。为了解决这一问题并且不增加模式的复杂性和训练难度,TransH被提出,其基本思想是将关系解释为超平面上的转换操作。每个关系都有两个向量,超平面的范数向量Wr和超平面上的平移向量dr,把每个head向量(h)和tail向量(t)投影到超平面上,得到新的向量(h⊥和t⊥)。在这个超平面中存在一个关系(d_r),可以像TransE模型一样训练它。
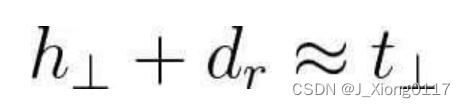
对应得分函数:
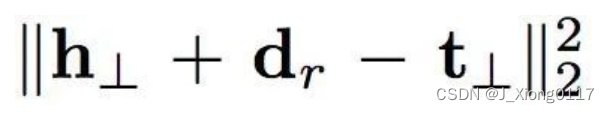
-
相关阅读:
超火的低代码平台长什么样
多模态相关论文笔记
cmmi3级和5级之间的区别是什么?
混合SDN中的安全性问题研究
执行Hive查询时出现OOM
Anycast CLB 如何支持多地&动态加速的负载均衡服务,高速互联转发!
[附源码]计算机毕业设计JAVAjava航班资源车管理系统
大一新生必备电脑软件&插件有哪些?
【LeetCode】53. 最大子数组和
跨境物流美国专线的注意事项是哪些
- 原文地址:https://blog.csdn.net/u013010473/article/details/126309245