扩展欧几里得

扩展欧几里得，常用于计算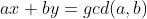的一组可行解

设,

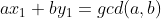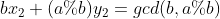
由欧几里得可知

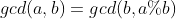
因此

又因为a mod b = 

所以

可得

因为a=a,b=b，所以,

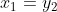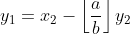
将不断代入递归求解直至gcd为0递归x=1，y=0回去求解

[NOIP2012 提高组] 同余方程 - 洛谷

求解方程最小正整数解，先把题目的方程分解来看，然后因为x和y的符号都是由我们决定的，所以可以得到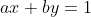,题面指出输入数据一定有解，因此从扩展欧几里得可知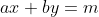，中如果有解，那么一定存在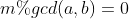,因此可得出题目中a和b一定互素，该题不能直接费马小定理求在mod b下的逆元，因为并没有保证b是质数

AC代码：

#include 
#define rep(i,a,n) for(int i=a;i
using namespace std;
using LL = long long;
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    int a, b, x, y;
    cin >> a >> b;
    function<int(int, int, int&, int&)> exgcd = [&](int a, int b, int &x, int &y) {
        if (!b) {
            x = 1;
            y = 0;
            return a;
        }
        int d = exgcd(b, a % b, x, y);
        int t = x;
        x = y;
        y = t - (a / b) * y;
        return d;
    };
    int g = exgcd(a, b, x, y);
    cout << (x + b) % b << '\n';
 
    return 0;
}