金仓数据库 KingbaseGIS 使用手册（6.16. 聚类函数）

6.16. 聚类函数

6.16.1. ST_ClusterDBSCAN

ST_ClusterDBSCAN — 基于 2D 空间中的 Density-based spatial clustering of applications with noise (DBSCAN) 算法返回每个输入几何对象的聚类号。 与 ST_ClusterKMeans 函数不同，该算法不需要预先指定聚类数，而是基于期望距离（eps）和密度（minpoints）参数来生成每个聚类。

用法

integer ST_ClusterDBSCAN(geometry winset geom, float8 eps, integer minpoints);

描述

基于 2D 空间中的 Density-based spatial clustering of applications with noise (DBSCAN) 算法返回每个输入几何对象的聚类号。 与 ST_ClusterKMeans 函数不同，该算法不需要预先指定聚类数，而是基于期望距离（eps）和密度（minpoints）参数来生成每个聚类。

一个输入的几何对象满足下列条件之一时，将会被加入一个聚类：

• 它距离至少 minpoints 个输入几何对象（包括它自己）的距离小于 eps，会被作为“核心对象 ”加入；

• 它距离一个“核心对象” 的距离小于 eps，会被作为一个“边界对象”加入；

需要注意的是，边界对象可能位于多个聚类的核心对象的 eps 距离内。在这种情况下，无论分到哪个类别下都是正确的，并且边界对象会被分配到其中任意一个类别下。 这有可能使得生成的正确类别所包含的几何对象数小于 minpoints。 当边界对象的分类存在歧义时， 如果在窗口定义中包含 Order By 子句，反复调用ST_ClusterDBSCAN 将能产生一致的结果，但可能与同一算法的其他实现返回的结果不同。

注意

无法满足聚类条件的输入几何对象，其聚类号将为 NULL。

样例

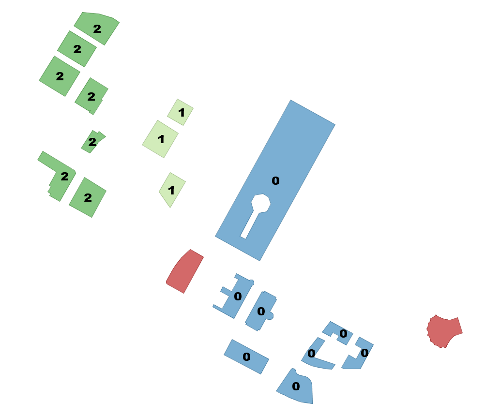
每个类别至少 包含 2 个对象，且对象间距在 50m 以内，孤立对象的 cid 为 NULL

SELECT name, ST_ClusterDBSCAN(geom, eps := 50, minpoints := 2) over () AS cid
FROM boston_polys
WHERE name > '' AND building > ''
   AND ST_DWithin(geom,
      ST_Transform(
            ST_GeomFromText('POINT(-71.04054 42.35141)', 4326), 26986),
         500);

               name                 | bucket
-------------------------------------+--------
Manulife Tower                      |      0
Park Lane Seaport I                 |      0
Park Lane Seaport II                |      0
Renaissance Boston Waterfront Hotel |      0
Seaport Boston Hotel                |      0
Seaport Hotel & World Trade Center  |      0
Waterside Place                     |      0
World Trade Center East             |      0
100 Northern Avenue                 |      1
100 Pier 4                          |      1
The Institute of Contemporary Art   |      1
101 Seaport                         |      2
District Hall                       |      2
One Marina Park Drive               |      2
Twenty Two Liberty                  |      2
Vertex                              |      2
Vertex                              |      2
Watermark Seaport                   |      2
Blue Hills Bank Pavilion            |   NULL
World Trade Center West             |   NULL
(20 rows)

使用命名参数绑定的方式调用，将同一类别中的几何对象合并成一个图块。

SELECT cid, ST_Collect(geom) AS cluster_geom, array_agg(parcel_id) AS ids_in_cluster FROM (
   SELECT parcel_id, ST_ClusterDBSCAN(geom, eps := 0.5, minpoints := 5) over () AS cid, geom
   FROM parcels) sq
GROUP BY cid;

参考

ST_DWithin, ST_ClusterKMeans, ST_ClusterIntersecting, ST_ClusterWithin

6.16.2. ST_ClusterIntersecting

ST_ClusterIntersecting — 将给定几何对象集合中相互之间存在交集的对象聚合成一类，返回一个由几何对象集合组成的数组。 每个数组元素代表一个类别。

用法

geometry[] ST_ClusterIntersecting(geometry set g);

描述

ST_ClusterIntersecting 是一个聚合函数。它返回一个由几何对象集合组成的数组，每个 几何对象集合代表一组相互之间有交集的几何对象。

样例

WITH testdata AS
(SELECT unnest(ARRAY['LINESTRING (0 0, 1 1)'::geometry,
            'LINESTRING (5 5, 4 4)'::geometry,
            'LINESTRING (6 6, 7 7)'::geometry,
            'LINESTRING (0 0, -1 -1)'::geometry,
            'POLYGON ((0 0, 4 0, 4 4, 0 4, 0 0))'::geometry]) AS geom)

SELECT ST_AsText(unnest(ST_ClusterIntersecting(geom))) FROM testdata;

--result

st_astext
---------
GEOMETRYCOLLECTION(LINESTRING(0 0,1 1),LINESTRING(5 5,4 4),LINESTRING(0 0,-1 -1),POLYGON((0 0,4 0,4 4,0 4,0 0)))
GEOMETRYCOLLECTION(LINESTRING(6 6,7 7))

参考

ST_ClusterDBSCAN, ST_ClusterKMeans, ST_ClusterWithin

6.16.3. ST_ClusterKMeans

ST_ClusterKMeans — 根据给定的聚类数，采用 K-Means 算法进行聚类，返回每个输入的几何对象到聚类中心的距离。

用法

integer ST_ClusterKMeans(geometry winset geom, integer number_of_clusters);

描述

基于 K-Means 聚类数，返回每个输入几何对象到聚类中心的距离。 对于 2D 几何对象， 返回的是其几何中心到所属类别中心的距离；对于 3D 几何对象， 返回的是其边界盒中心到所属类别中心的距离。 对于输入的 POINT 对象， M 坐标被视为权重值， 因此必须大于 0。

样例

CREATE TABLE parcels AS
SELECT lpad((row_number() over())::text,3,'0') As parcel_id, geom,
('{residential, commercial}'::text[])[1 + mod(row_number()OVER(),2)] As type
FROM
   ST_Subdivide(ST_Buffer('SRID=3857;LINESTRING(40 100, 98 100, 100 150, 60 90)'::geometry,
   40, 'endcap=square'),12) As geom;

原始图块

基于聚类号（cid）作颜色编码后的图块

SELECT ST_ClusterKMeans(geom, 5) OVER() AS cid, parcel_id, geom
FROM parcels;
-- result
cid | parcel_id |   geom
-----+-----------+---------------
   0 | 001       | 0103000000...
   0 | 002       | 0103000000...
   1 | 003       | 0103000000...
   0 | 004       | 0103000000...
   1 | 005       | 0103000000...
   2 | 006       | 0103000000...
   2 | 007       | 0103000000...
(7 rows)

-- Partitioning parcel clusters by type
SELECT ST_ClusterKMeans(geom,3) over (PARTITION BY type) AS cid, parcel_id, type
FROM parcels;
-- result
cid | parcel_id |    type
-----+-----------+-------------
   1 | 005       | commercial
   1 | 003       | commercial
   2 | 007       | commercial
   0 | 001       | commercial
   1 | 004       | residential
   0 | 002       | residential
   2 | 006       | residential
(7 rows)
-- Clustering points around antimeridian can be done in 3D XYZ CRS, EPSG:4978:

SELECT ST_ClusterKMeans(ST_Transform(ST_Force3D(geom), 4978), 3) over () AS cid, parcel_id, type
FROM parcels;
-- result
┌─────┬───────────┬─────────────┐
│ cid │ parcel_id │    type     │
├─────┼───────────┼─────────────┤
│   1 │ 001       │ commercial  │
│   2 │ 002       │ residential │
│   0 │ 003       │ commercial  │
│   1 │ 004       │ residential │
│   0 │ 005       │ commercial  │
│   2 │ 006       │ residential │
│   0 │ 007       │ commercial  │
└─────┴───────────┴─────────────┘
(7 rows)

参考

ST_ClusterDBSCAN, ST_ClusterIntersecting, ST_ClusterWithin, ST_Subdivide

6.16.4. ST_ClusterWithin

ST_ClusterWithin — 返回一个几何对象集合数组，每个集合都由一组相距不超过指定距离几何对象构成。 （距离采用 SRID 指定的坐标系中的笛卡儿距离）

用法

geometry[] ST_ClusterWithin(geometry set g, float8 distance);

描述

ST_ClusterWithin 是一个聚合函数。它返回一个几何对象集合数组，每个集合都由一组相距不超过指定距离几何对象构成。（距离采用 SRID 指定的坐标系中的笛卡儿距离）。

样例

WITH testdata AS
(SELECT unnest(ARRAY['LINESTRING (0 0, 1 1)'::geometry,
            'LINESTRING (5 5, 4 4)'::geometry,
            'LINESTRING (6 6, 7 7)'::geometry,
            'LINESTRING (0 0, -1 -1)'::geometry,
            'POLYGON ((0 0, 4 0, 4 4, 0 4, 0 0))'::geometry]) AS geom)

SELECT ST_AsText(unnest(ST_ClusterWithin(geom, 1.4))) FROM testdata;

--result

st_astext
---------
GEOMETRYCOLLECTION(LINESTRING(0 0,1 1),LINESTRING(5 5,4 4),LINESTRING(0 0,-1 -1),POLYGON((0 0,4 0,4 4,0 4,0 0)))
GEOMETRYCOLLECTION(LINESTRING(6 6,7 7))

参考

ST_ClusterDBSCAN, ST_ClusterKMeans, ST_ClusterIntersecting