PR控制器

PR控制器原理

系统在双闭环控制过程中通常使用传统的 PI 控制器,但是电网在基波处的增益是有限值,PI 控制器能够实现对直流信号的无静差追踪,却并不能在正弦信号的追踪过程中实现无静差,相应产生的稳态误差会造成追踪电流 在有效值幅值和相位上的误差。电流有效值幅值上的误差,可以通过增大控制器的比例系数,相应的增大基波频 率的增益来实现,但是并不能完全的消除误差,仍是有差调节。在幅值误差得到有效改善的情况下,系统的误差主要表现为相位误差,需要通过控制器的改进来减小相位的误差值。
根据 PR 控制器在跟踪控制方面的优势,用PR控制器替代 PI 控制器,在系统加载冲击性负载时,可以有很好的响应速度,保证了系统良好的动态稳定性。
下面给出 PR 控制器的传递函数以及对应的基波 频率处的增益:

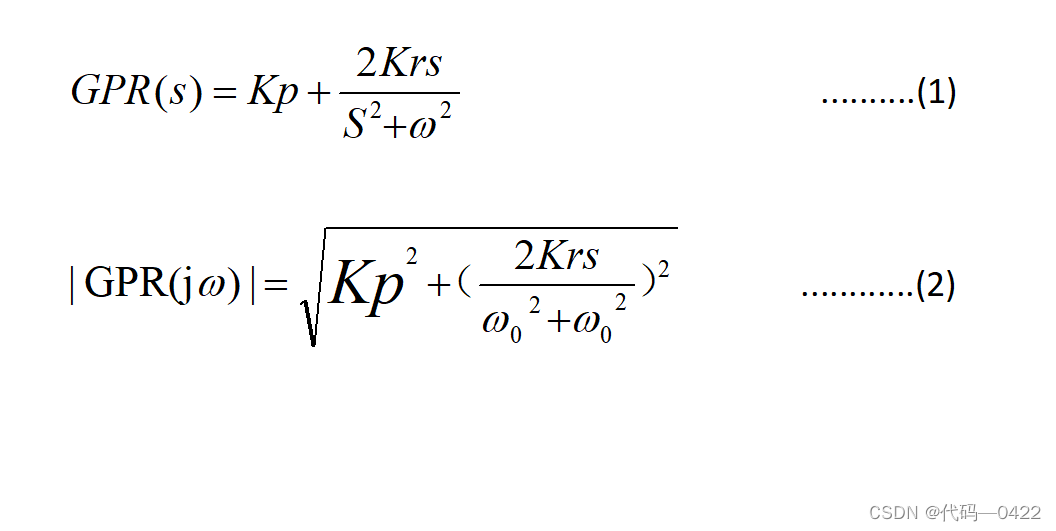
根据式(1)(2)可以看出,由于基波频率处的增益趋于无穷大,使系统在追踪固定频率正弦信号时能够实现无静差追踪。

在实际应用中,虽然 PR 控制在基波频率处拥有较高 的增益,但是相角裕度较小,带宽较窄,引起系统发生振 荡,容易造成控制器谐振频率的偏移,影响系统稳定。为了增大相角裕度和带宽宽度,可通过添加增益较高的低通 滤波器实现,从而构成了准比例谐振(PR)控制,准 PR 控 制器的传递函数如式(3)所示:

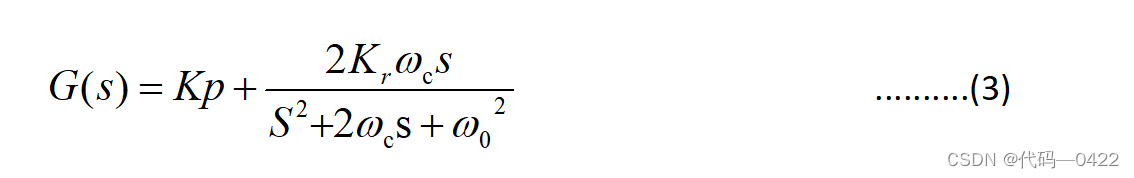
式中:Kp ,Kr,ωc 为控制器参数,ω0=314 rad/s。
PI 控制PR 控制和准 PR 控制的频率特性如图所示。
kp=10 ， ki =kr=100；

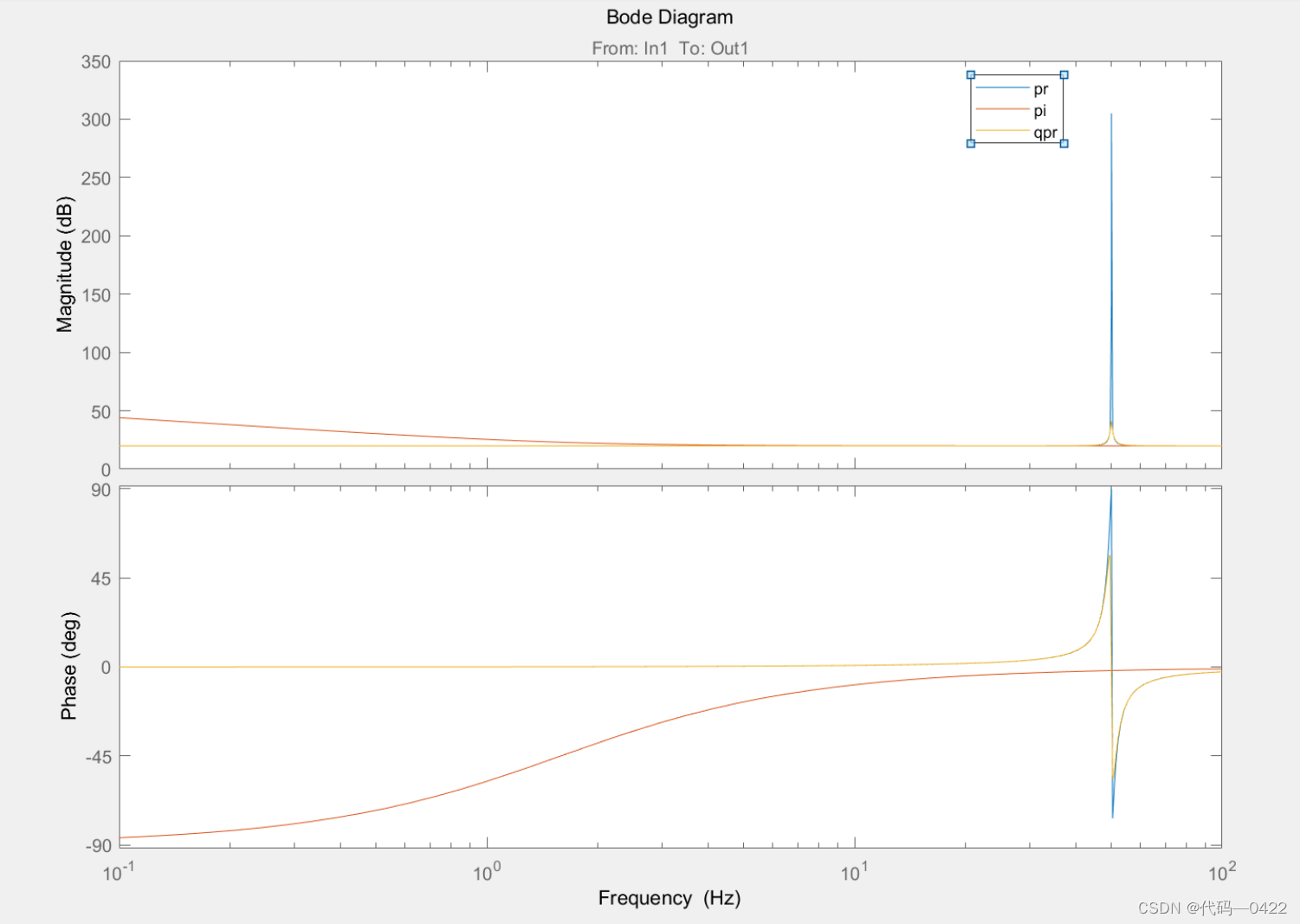
图中,PI 控制器在基波频率处的增益几乎为零,而PR控制器与准PR 控制器在基波频率处的增益却很大, 且具有相似的频率特性,可以在指定的频率下对稳态误差 进行有效的消除,故可利用准PR控制器来代替PI控制器,从而在消除幅值误差的同时消除相位误差,做到对指 定信号的准确追踪,消除了稳态误差。

准 PR 控制器的设计

通过对准PR控制器的传递函数的分析,可以明确在 控制器参数的设计过程中,主要是对 Kp ,Kr,ωc 进行选 择,所以本文首先使用控制变量的方法来对各个参数的作用进行分析。

首先令 K p 2 =0,ωc =1,同时使 Kr 不断变化,对应的频 率特性如图 4 所示。
Kr1=10
Kr2=100
Kr3=1000
Kr4=10000

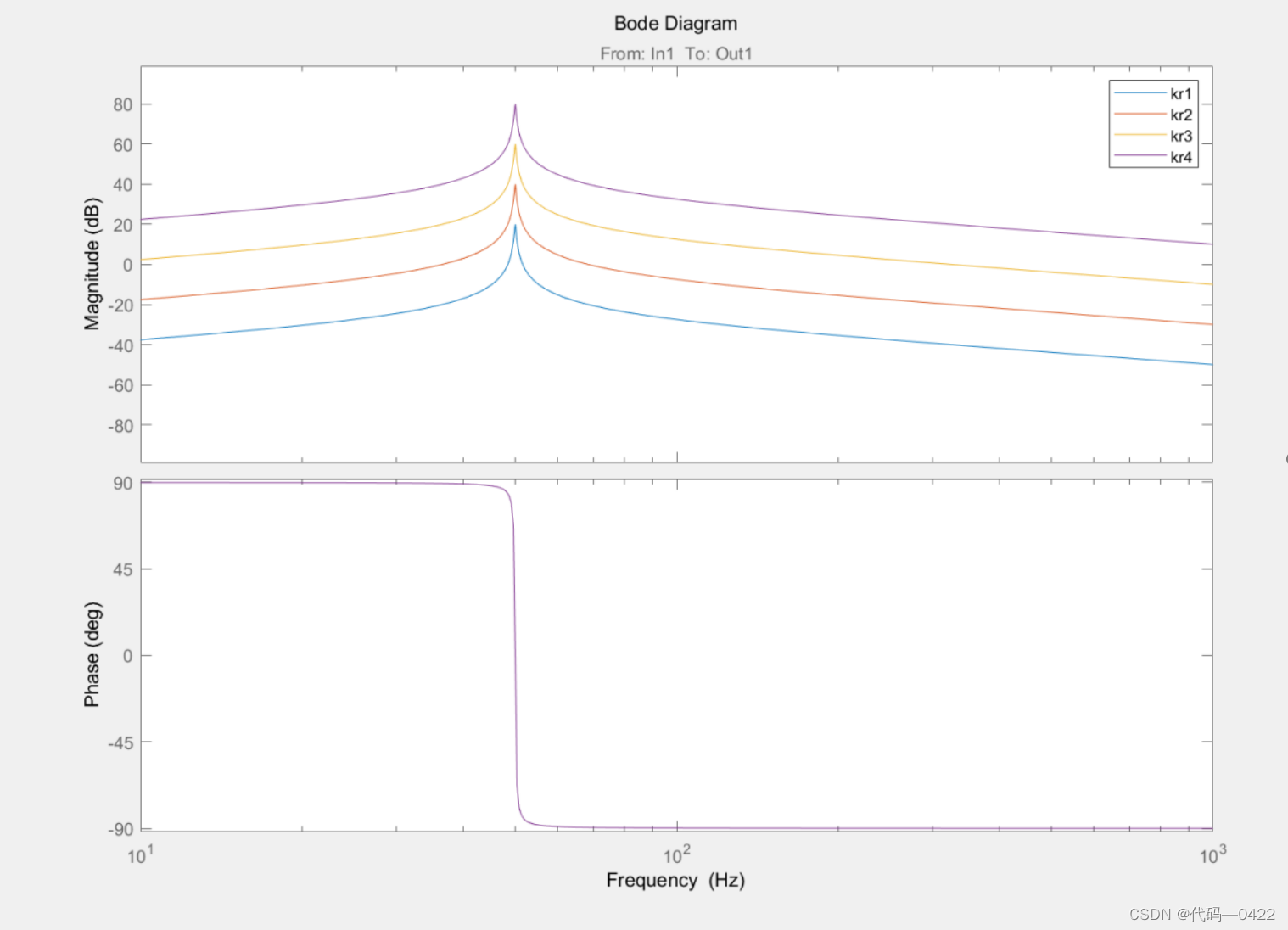
由图 可知,在参数 Kr 的变化过程中,只有控制器的增益相应的进行变化,并且随着 Kr 的增大,控制器的增益 增大的同时,稳定性不断加强,但却不会对控制器的带宽 造成影响。然而 Kr 增大到一定程度就会引起谐波分量的放大,所以要合理的选择参数 Kr,既满足基波频率处有较 大的增益,又能具有一定的衰减性。

令 Kp=0,Kr=1,ωc 进行不断变化,对应的频率特性如图所示。
Wc =1,
Wc =5,
Wc =15，
Wc =30,
Wc =50，

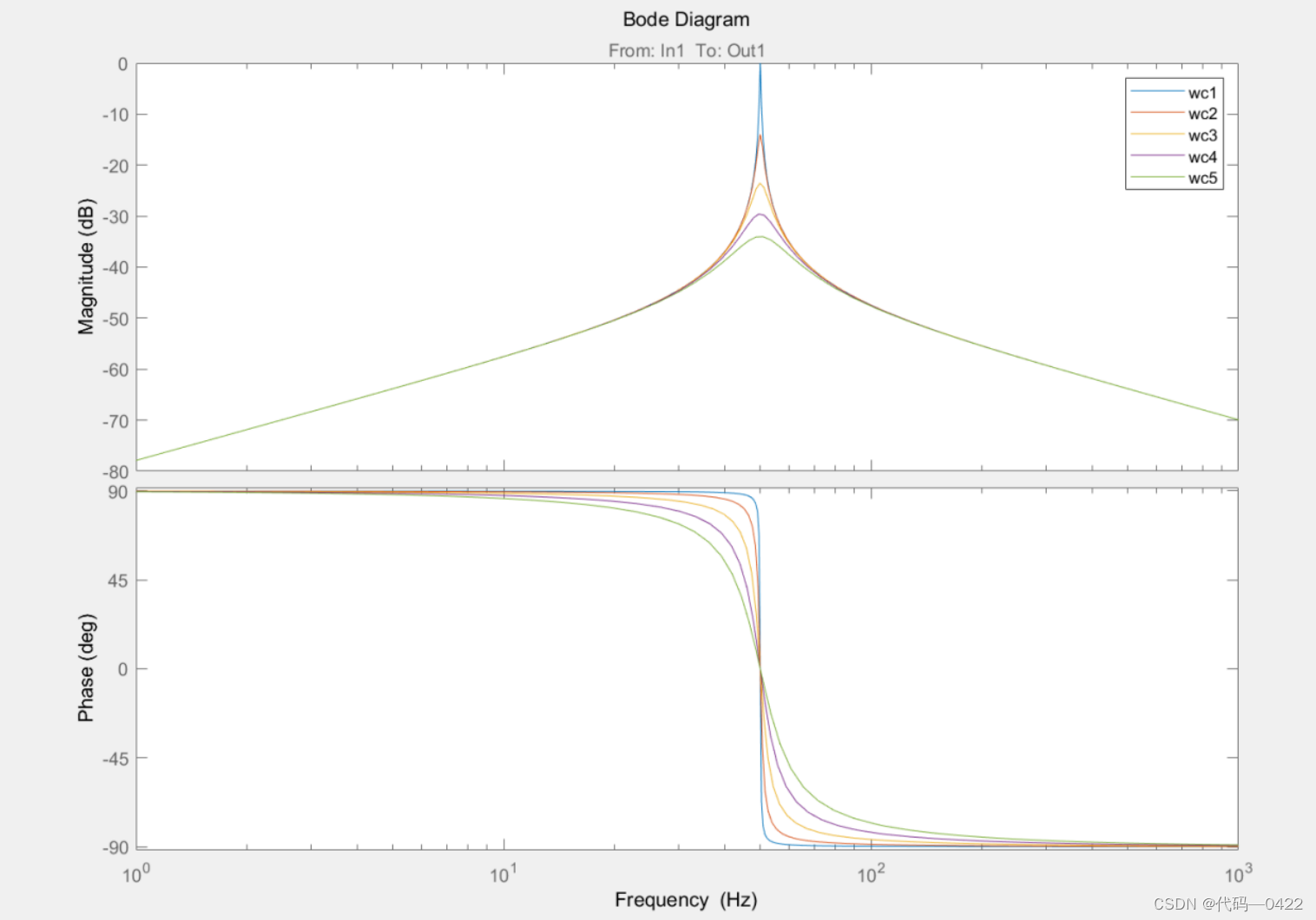
从图 5 中可得,在参数ωc 变化过程中,控制器的增益 与带宽同时发生变化,说明ωc 对两者都存在相关性,虽然 随着ωc 的增大,控制器基波频率处的增益未发生改变,但 控制器非基波频率处的增益和带宽却同时变大,所以参数 ωc 的选择需要根据频率的波动和控制器带宽的需求共同 决定。

在分析 Kp变化之前,先令 Kp =0,并将 jω=s 带入到（3）中,得到

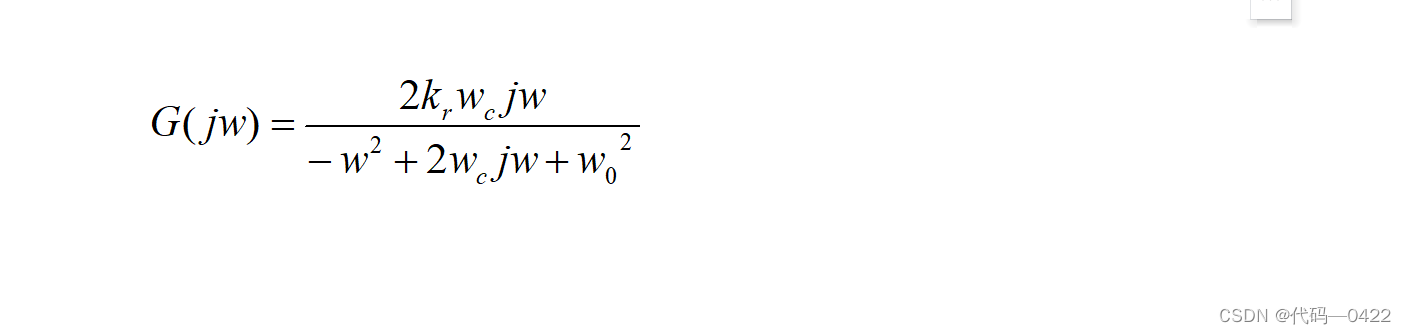
令上式中的ω0/2ωc=Q,则 Q 看作 PR 控制器谐振环节 的品质系数。
设电网允许的频率波动是±0.5 Hz,此时的控制器带 宽为 d=1 Hz，
,在 |Q （ω/ω0 -ω0/ ω） | =1 时可得频率之间相差带宽为 d = ωc /2πQ = ωc/ π,对应的ωc =3.14。

最后令 Kr=100,ωc =3.14,K p 进行变化,对应的频率特性如图 所示
kp= 0.1 ，
kp= 1 ，
kp= 10，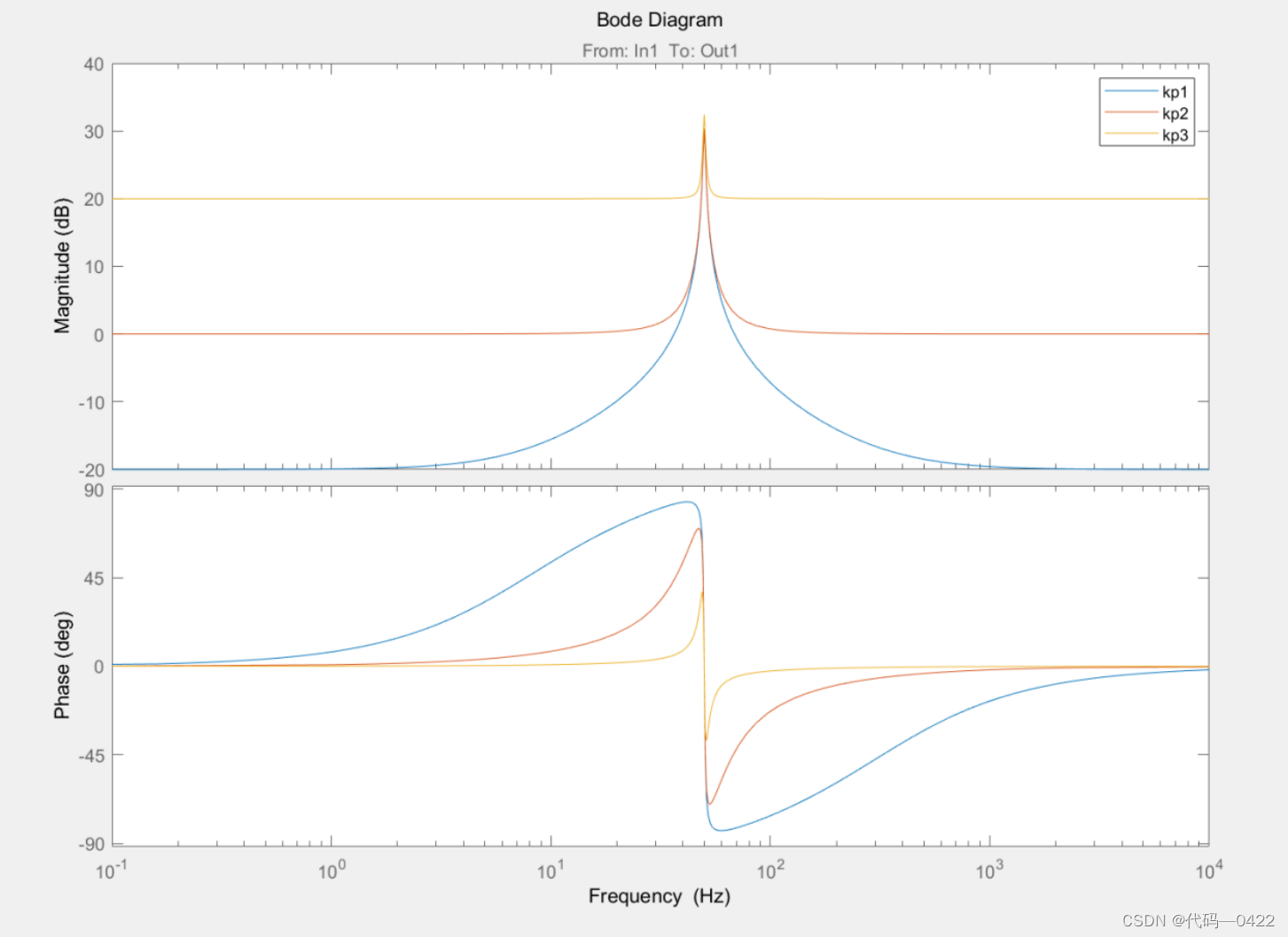

根据上图 的变化,控制器的增益与带宽都受到 Kp变化的影响,但是随着 Kp 的增大,控制器增益在基波频率 处的增益并未发生改变,只在非基波频率处增益相应的增 大,对应的带宽随着 Kp的增大而减小。所以随着 Kp 的 不断增大,使系统的抗干扰能力不断增强,但是并不能无 限增大,若 K p 2 过大会造成系统的振荡而影响其稳定性。计根据对控制器各个参数的分析,准 PR 控制参数的设 一般需要按照以下步骤设计[1 3]:
1)ωc 值的确定,此值主要与系统截止频率的带宽需求有关;
2)Kr 值的确定,此值主要根据系统所需的峰值增益 的大小来进行取值;
3)Kp值的确定,此值主要根据系统对比例增益的要求来选择最佳的Kp 值。
按照上述步骤设计的控制器参数,使准 PR 控制器系 统具有很强的稳定性与抗干扰性,系统的控制效果达到最佳。根据本系统实际实验过程的需要,选择的准 PR 控制 参数如下:Kp=6.5,Kr =120,ωc=8,得到的准PR控制器 Bode 图如图 所示。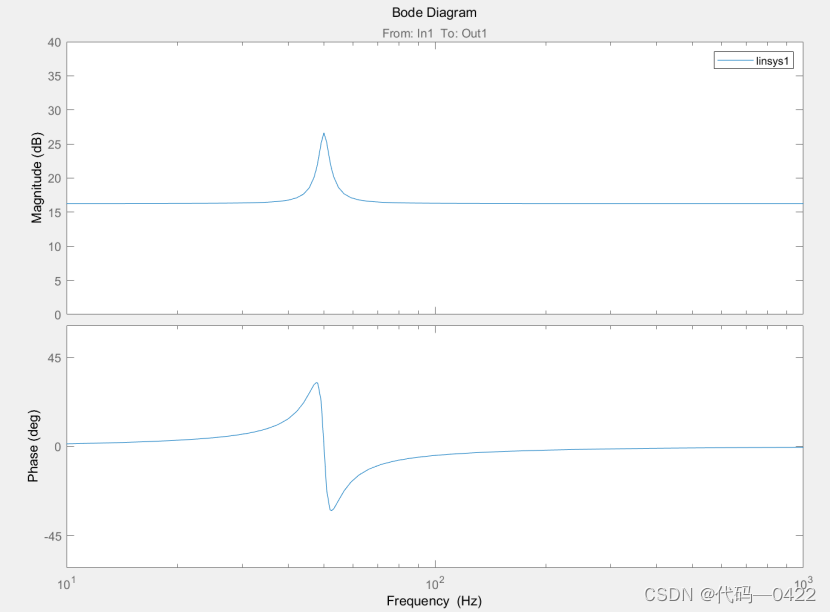

准 PR 控制的谐波补偿环

为了增强系统的抗干扰能力,在准 PR 控制器中增加 各个主要频次谐波的谐振补偿环,使系统在谐波频率点处产生较大的增益,同时保证系统有足够的相角裕度和良好的动态性能。根据实际中谐振补偿方式的需要合理进行选择,谐振补偿环的传递函数为:

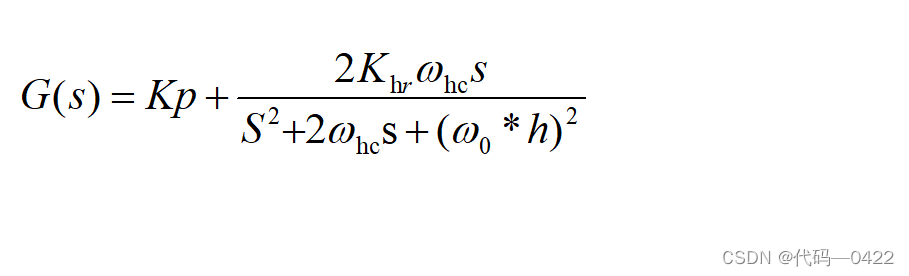
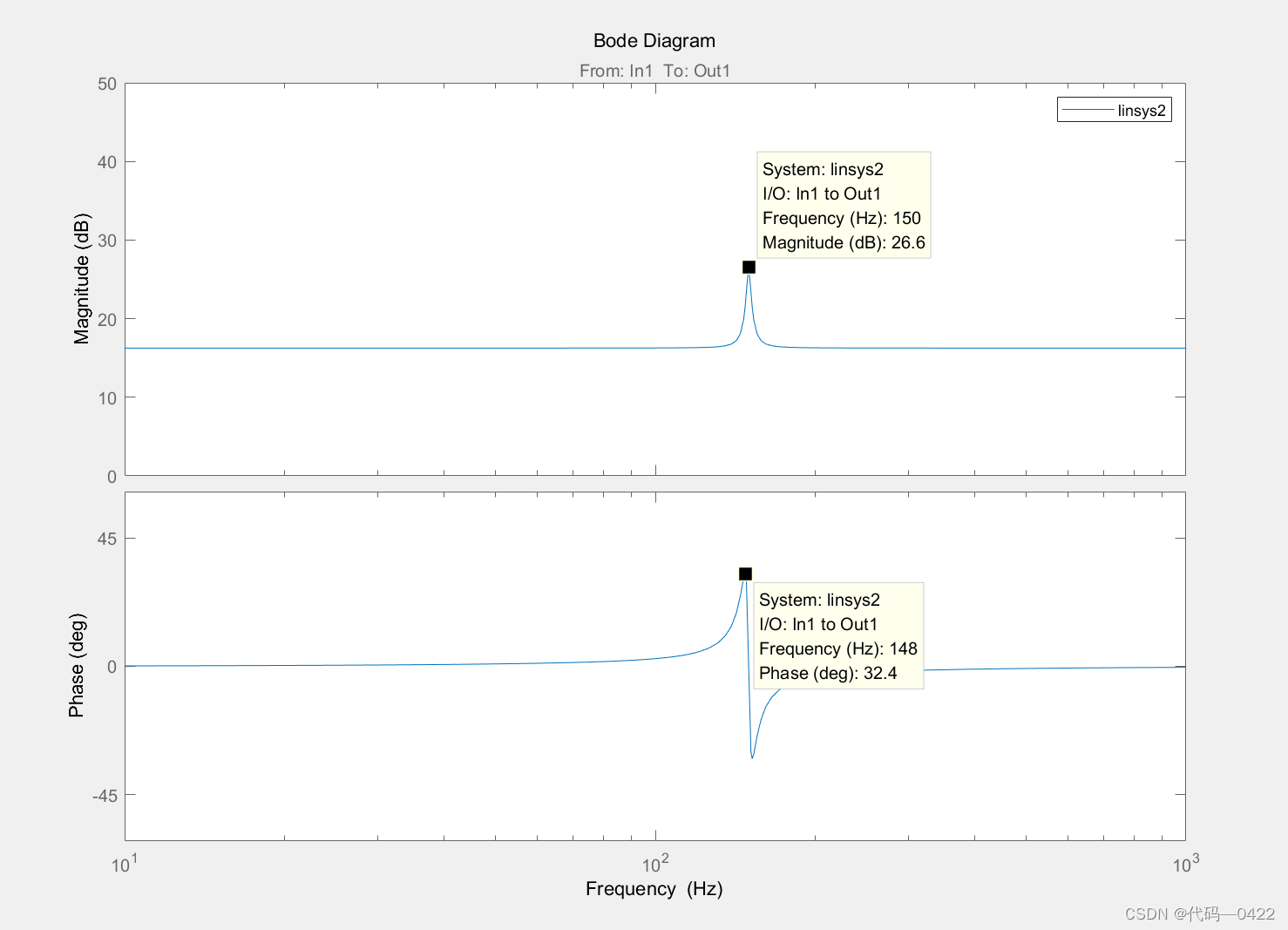
下面以 3 次谐波为例,如图所示。在准 PR 控制器 中添加 3 次谐波补偿环,并画出对应的 Bode 图。添加了谐波补偿环后,对应的谐波频率处产生了很大增益,实现了对应谐波的无静差追踪,同时抑制了谐波对系统电能质 量的影响。一般情况下,通过添加特定次数的谐波补偿 环,在实现对基波成分跟踪的同时,还能对特定次数的谐 波成分进行跟踪,实现对特定次数谐波的消除,从而减小了谐波造成的污染,提高了逆变器系统的电能质量。