【无人机】基于A星算法解决无人机二维路径规划问题含matlab代码

1 内容介绍

无人机路径规划一直是一个比较热门的话题,A星算法以及其扩展性算法被广范地应用于求解无人机的最优路径.该文在研究无人机路径规划算法中,详细阐述了传统A星算法的基本原理,并通过栅格法分割了机器人路径规划区域,利用MATLAB仿真平台生成了无人机二维路径仿真地图对其进行仿真实验,并对结果进行分析和研究,为今后进一步的研究提供经验.​

2 仿真代码

%%%%%%%****Astar算法

clc;

clear all;

close all

MAX_X=30;

MAX_Y=10;

MAX_VAL=20;

MAP=2*(ones(MAX_X,MAX_Y));

%初始化地图

j=0;

x_val = 1;

y_val = 1;

axis([1 MAX_X 1 MAX_Y])

% set(gca,'XTick',0:1:30);

hold on;

%%%%%%%%%%%%%%%%%%%%%%%二维地图生成完毕%%%%%%%%%%%%%

xStart=2;%起始地点

yStart=3;

MAP(xStart,yStart)=1;

 plot(xStart+0.5,yStart+0.5,'go');

text(xStart+1,yStart+.5,'起始点')

%设置障碍

for xval=1:30;

    for yval=8:10;   

    

    MAP(xval,yval)=-1;%

    rectangle('Position',[xval,yval,1,1],'facecolor',[0.1,0.2,0.3])

    end

end

for xval=1:30;

    for yval=1:2;   

    

    MAP(xval,yval)=-1;%

    rectangle('Position',[xval,yval,1,1],'facecolor',[0.1,0.2,0.3])

    end

end

%设置障碍的长度、高度

for xval=8:18;

    for yval=3:5;   

    

    MAP(xval,yval)=-1;%

    rectangle('Position',[xval,yval,1,1],'facecolor',[0.1,0.2,0.3])

    end

end

%设定目的坐标

xTarget=29;%

yTarget=3;

 plot(xTarget+0.5,yTarget+0.5,'ro');

text(xTarget+1,yTarget+.5,'结束点')

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%开始执行A*算法计算最优化路径%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

OPEN=[];

CLOSED=[];

%载入地图数据

k=1;

for i=1:MAX_X

    for j=1:MAX_Y

        if(MAP(i,j) == -1)

            CLOSED(k,1)=i; 

            CLOSED(k,2)=j; 

            k=k+1;

        end

    end

end

CLOSED_COUNT=size(CLOSED,1);

%设置出发位置

xNode=xStart;

yNode=yStart;

OPEN_COUNT=1;

path_cost=0;

goal_distance=distance(xNode,yNode,xTarget,yTarget);

OPEN(OPEN_COUNT,:)=insert_open(xNode,yNode,xNode,yNode,path_cost,goal_distance,goal_distance);

OPEN(OPEN_COUNT,1)=0;

CLOSED_COUNT=CLOSED_COUNT+1;

CLOSED(CLOSED_COUNT,1)=xNode;

CLOSED(CLOSED_COUNT,2)=yNode;

NoPath=1;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 算法开始计算

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

while((xNode ~= xTarget || yNode ~= yTarget) && NoPath == 1)

 exp_array=expand_array(xNode,yNode,path_cost,xTarget,yTarget,CLOSED,MAX_X,MAX_Y);

 exp_count=size(exp_array,1);

 %更新数据

 for i=1:exp_count

    flag=0;

    for j=1:OPEN_COUNT

        if(exp_array(i,1) == OPEN(j,2) && exp_array(i,2) == OPEN(j,3) )

            OPEN(j,8)=min(OPEN(j,8),exp_array(i,5));

            if OPEN(j,8)== exp_array(i,5)

                

                OPEN(j,4)=xNode;

                OPEN(j,5)=yNode;

                OPEN(j,6)=exp_array(i,3);

                OPEN(j,7)=exp_array(i,4);

            end;

            flag=1;

        end;

    end;

    if flag == 0

        OPEN_COUNT = OPEN_COUNT+1;

        OPEN(OPEN_COUNT,:)=insert_open(exp_array(i,1),exp_array(i,2),xNode,yNode,exp_array(i,3),exp_array(i,4),exp_array(i,5));

     end;%

 end;

  index_min_node = min_fn(OPEN,OPEN_COUNT,xTarget,yTarget);

  if (index_min_node ~= -1)    

   

   xNode=OPEN(index_min_node,2);

   yNode=OPEN(index_min_node,3);

   path_cost=OPEN(index_min_node,6);%更新路径代价值

  

  CLOSED_COUNT=CLOSED_COUNT+1;

  CLOSED(CLOSED_COUNT,1)=xNode;

  CLOSED(CLOSED_COUNT,2)=yNode;

  OPEN(index_min_node,1)=0;

  else

      

      NoPath=0;

  end;

end;

%%%%%%输出最优化路径坐标

i=size(CLOSED,1);

Optimal_path=[];

xval=CLOSED(i,1);

yval=CLOSED(i,2);

i=1;

Optimal_path(i,1)=xval;

Optimal_path(i,2)=yval;

i=i+1;

if ( (xval == xTarget) && (yval == yTarget))

    inode=0;

   

   parent_x=OPEN(node_index(OPEN,xval,yval),4);

   parent_y=OPEN(node_index(OPEN,xval,yval),5);

   

   while( parent_x ~= xStart || parent_y ~= yStart)

           Optimal_path(i,1) = parent_x;

           Optimal_path(i,2) = parent_y;

          

           inode=node_index(OPEN,parent_x,parent_y);

           parent_x=OPEN(inode,4);

           parent_y=OPEN(inode,5);

           i=i+1;

    end;

    

    

else

    

    path_cost=1000000;%不存在最优化路径

end

  

 j=size(Optimal_path,1);

 Optimal_path(j,1)=xStart;

 Optimal_path(j,2)=yStart;

  

 x=Optimal_path(:,1)+0.5;

 y=Optimal_path(:,2)+0.5;

 for i=2:length(y)-1;

     if y(i)>yTarget+0.5;

            y(i)=y(i)+0.5;

     end

 end

 xi=Optimal_path(end,1)+0.5:0.1:Optimal_path(1,1)+0.5;  

yi=spline(x,y,xi);

plot(xi,yi,'r','LineWidth',1);

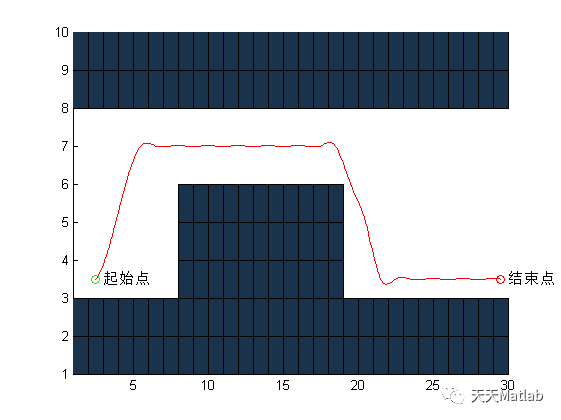
3 运行结果

4 参考文献

[1]董箭, 初宏晟, 卢杬樟,等. 基于A星算法的无人机路径规划优化模型研究[J]. 海洋测绘, 2021, 41(3):5.

[2]周宇杭, 王文明, 李泽彬,等. 基于A星算法的移动机器人路径规划应用研究[J]. 电脑知识与技术：学术版, 2020, 16(13):4.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。