静态优化

动态优化解决的问题是传统的拉格朗日函数方法（静态等式约束问题）以及Kuhn-tucker方法（静态不等式约束问题）无法解决的动态问题，在宏观经济学中主要是涉及离散和连续的涉及时间的变化的问题

动态优化

HJB方程是连续时间最优控制的充分必要条件。

Hamilton函数 无约束最优控制

有约束：内点法

最近邻向量量化器 Nearest Neighbor Vector Quantizer

给定一个可数的（不一定是有限的）非相等向量集B={b1,b2,...}⊂RnB" role="presentation" style="position: relative;">B={b1,b2,...}⊂RnB$B=\left\{b_1,b_2,...\right\}\subset {\mathbb{R}}^{n_B}$，最近邻向量量化器定义为一个映射qB" role="presentation" style="position: relative;">qB$q_B$

使用NNVQ得到的最优控制律是时变非线性的状态反馈控制律 

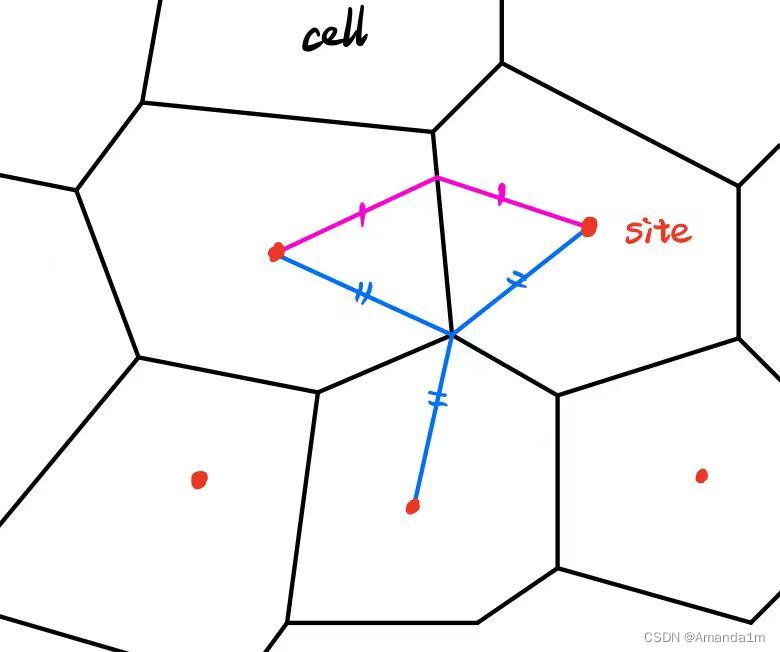
沃罗诺伊图 Voronoi partition

放大多个圆相交得到的晶胞（cell）有以下性质：

1. 每一条边到最近的两个圆心（site）的距离相等（边是两sites构成线段的中垂线）
2. 每条边相交的点到最近的三个圆心（site）距离相等

饱和约束 Saturation constraints

输入饱和是定义在l∞" role="presentation" style="position: relative;">l∞$l_{\mathrm{\infty }}$范数上的凸问题，状态空间被划分为多面体，其中滚动时域控制器在状态上是分段仿射的。

l∞" role="presentation" style="position: relative;">l∞$l{}_{\mathrm{\infty }}$约束的最优解u~⋆(x(k))" role="presentation" style="position: relative;">u~⋆(x(k))${\tilde{u}}^{\star }\left(x\left(k\right)\right)$和无约束的最优解u~uc⋆(x(k))" role="presentation" style="position: relative;">u~⋆uc(x(k))${\tilde{u}}_{uc}^{\star }\left(x\left(k\right)\right)$是由最小欧式距离投影得到的。

稳定性

为了建立具有离散控制集的MPC控制的LTI系统的实际稳定性，我们将(二次)MPC代价函数作为一个候选的实际-李雅普诺夫函数，并利用代数Riccati方程设计终端代价。基于凸控制集设计了相应的终端区域。原始的离散输入字母集成为该凸集的量化。选择局部控制器为一步最优解。因此，我们可以通过将所提出的局部控制器产生的量化误差视为有界扰动来刻画一个最终有界的不变量集Dδ" role="presentation" style="position: relative;">Dδ$D_{\delta }$。此外，我们建立了充分的条件来保证这个最终有界不变集是终端区域的子集。这加上精心设计的终端成本，使我们能够建立渐近实际稳定的预测策略。

K-函数 K-function

“practical" role="presentation" style="position: relative;">practical$practical$”一词用来强调只研究原点邻域的稳定性。后者的性质有时也被称为终极有界性

正不变集 Positively Invariant Set

一致实际渐近稳定 Uniformly practically Asymptotically Stable

Practical-Lyapunov函数

Theorem 1

如果系统(1)在A中找到一个实际的lLyapunov函数，那么在A中它就是UpAS的。

Matlab求解离散黎卡提方程

 ATPA−P−ATPB(BTPB+R)−1BTPA+Q=0" role="presentation" style="position: relative;">ATPA−P−ATPB(BTPB+R)−1BTPA+Q=0$A^{T}PA-P-A^{T}PB{\left(B^{T}PB+R\right)}^{-1}{B}^{T}PA+Q=0$

 等价于

(A−BK)TP(A−BK)+Q+KTRK−P=0" role="presentation" style="position: relative;">(A−BK)TP(A−BK)+Q+KTRK−P=0${\left(A-BK\right)}^{T}P\left(A-BK\right)+Q+K^{T}RK-P=0$

其中： 

 K=(BTPB+R)−1BTPA" role="presentation" style="position: relative;">K=(BTPB+R)−1BTPA$K={\left(B^{T}PB+R\right)}^{-1}{B}^{T}PA$

u(x)=−Kx" role="presentation" style="position: relative;">u(x)=−Kx$u\left(x\right)=-Kx$

Matlab函数求解：

[P,K,L] = idare(A,B,Q,R,[],[]);