题目：

Description

小J有很多空白的球和一个袋子。最初，袋子是空的。

小J将会作出Q个操作，具体如下：

操作1 在白球上写一个数字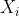然后扔进袋子里；

操作2 将袋子里所有球的数字都加上；

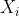操作3 输出袋子里最小的数字并把它从袋子里取出。

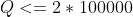
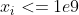
Format

Input

见样例

Output

针对每个操作3，输出结果

Samples

输入数据 1

5
1 3
1 5
3
2 2
3
 

输出数据 1

3
7
 

思路：

从”操作1“和 “操作3”不难看出，这道题要用堆来储存元素

但是第二个操作就有些棘手了

思路1：如果我们用每次将堆里存的元素取出来，再统一加上一个数,在全部装进堆里：

假设有堆里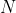个元素

每次操作的时间复杂度大概是

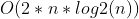
（注：堆的删除与插入的时间复杂度都是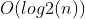的）

结合数据范围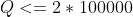，这种方法是绝对过不了的

 当时我们队里的人都懵B了，以为教练出错题了

思路2：这时我们的教练告诉了我们一个时间复杂度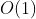的操作：

在上一个算法的基础上我们可以开一个懒标记，

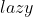针对每个“操作2”，我们可以在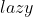加一个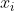

等到执行“操作3”时，再在弹出的堆顶加上一个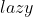就行了

可是这样做连后面进来的元素也会被打上标记

这时我们可以这样做：
针对每个“操作1”：将每个读入的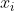，先减去一个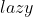，再打入堆中，这样就可以将前面的标记抵消掉。

Code：

#include
using namespace std;
//小根堆，每次弹出堆中最小值 
priority_queue<long long, vector<long long>, greater<long long> >a;
//操作 
int operate;
//懒标记 
long long lazy = 0;
long long num;
long long ans = 0;
int n;
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &operate);
		if (operate == 1)
		{
			scanf("%lld", &num);
			//插入 num-lazy 抵消前面的操作 
			a.push(num - lazy);
		}
		if (operate == 2)
		{
			scanf("%lld", &num);
			//标记加上num 
			lazy += num;
		}
		if (operate == 3)
		{
			//输出别忘了加上标记 
			printf("%lld\n", a.top() + lazy);
			a.pop();
		}
	}
	return 0;
}