LeetCode220811_81、柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

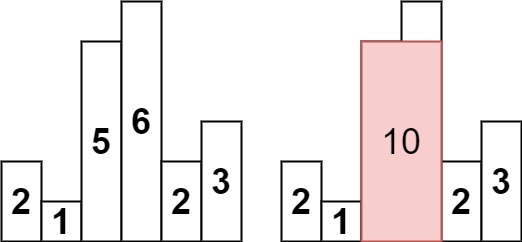
图1 柱状图中最大的矩形示例图

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/largest-rectangle-in-histogram
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解、矩形面积 = 底 * 高，底不好确定，高为各个元素的值，是确定的，根据高找到对应的最大的底，为其中一个元素的最大面积，所有的高度均找过最大面积，再从中选择最大即为题目所求。

使用哨兵，数组首尾各添加1个0元素，前面的0可保证按栈存储数据时，根据遍历元素小于栈顶元素才弹出栈顶元素的规则，栈必定不为空，后面的0可保证前面的数据能够全部弹出。

class Solution{
    public int largestRectangleArea(int[] heights){
        int len = heights.length;
        if(len == 0) return 0;
        if(len == 1) return heights[0];
        int[] newHeights = new int[len + 2];
        System.arraycopy(heights, 0, newHeights, 1, len);
        Deque stack = new ArrayDeque<>();
        stack.push(0);
        int res = 0;
        len += 2;
        heights = newHeights;
        for(int i = 1; i < len; i++){
            while(heights[i] < heights[stack.peek()]){
                int height = heights[stack.pop()];
                int width = i - stack.peek() - 1;
                res = Math.max(res, height * width);
            }
            stack.push(i);
        }
        return res;
    }
}