网络流中反向边作用

网络流常用算法 EK,Dinic 中都有一个重要的概念 反向边，指的是原本的网络中不存在的，为了求解 最大流、最小割问题 而虚拟出来的边，这样的边有一个重要作用，就是提供了 反悔 机制。

反悔机制的具体解释

首先我们来看这样的一个流量网络

在这样一个网络中，我们可以找到的一个 可行流 方案(1 -> 2 -> 4 -> 6)是这样的：

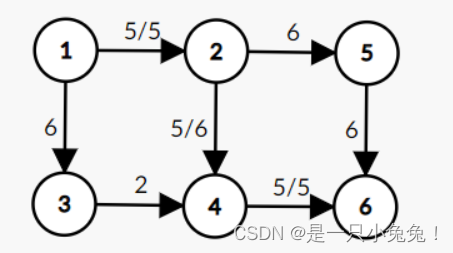
（注：图中斜杠/左边的数字为从该边实际流过的流量，右边的数字为该边允许通过的最大流量）

可以看到，按照该方案，可以证明我们在这样一个流量网络中，找不到更大的一个流量了，因为如果 按照该方案 做，已经无法找到新的任何一条路径，使得从 源点1 到 汇点6 的流量更大。

而增加了反向边后，即使我们按照该方案对流量网络进行操作，操作后我们将会得到这样的一个 残余网络

(注：图中斜杠左边的数字为从2到4的允许通过的最大流量为1，斜杠右边表示允许通过的从4到2的最大流量为5，流量为0的边不再画出)

有了反向边后，我们就可以从 1 出发，沿着 1-> 3 -> 4 -> 2 - > 5 -> 6的路径，从 源点1 出发走到 汇点6 ，并且该路径的最大可行流为 2。

于是，我们找到了一条新的从 源点1 出发走到 汇点6 的路径 1-> 3 -> 4 -> 2 - > 5 -> 6，路径的流量为 2。

再加上我们第一次选择的路径1 -> 2 -> 4 -> 6的流量5，可得最大流为7，并且可以证明，7就是这个流量网络的最大流。

有没有觉得很玄学？但其实，我们可以这样理解：

首先，我们先看一个最大流的可行方案：

（注：该图中做法为：一条路径从1 -> 3 -> 4 一条路从 1 -> 2 ，在2处发生分流，一条以2的流量从2走向5，再走向6，另外一条以3的流量，在4处与另外一条路上的流量汇合，以3 + 2 = 5的流量走向6）

接下来我们来解释一下，为什么反向边起到了 反悔 的作用

第一次我们选择的路径1 -> 2 -> 4 -> 6，流量为5，但是其实这个路径不够“好”，因为如果我们完全按照这个路径流5的流量的话，那么其实他“阻塞”了另外一条路（1-> 3 -> 4 -> 2 -> 5 -> 6）。这里的阻塞只是一个形象的说法，因为从4 -> 2的路径在原本的流量网络中是不存在的。

但是由于我们选择的路径一定是从 源点1 出发走到 汇点6 的一条路径，换言之这是一个可行流，因此我们知道这个流量网络的 最大流一定严格大于等于该可行流的流量。

因此，我们首先不妨假设，我们就走这条路，走完这条路之后，接下来我们开始找 新的一条路，如果没有反向边，我们此时是无法找到新的路径的，但是有了反向边，我们在4这个点，就可以 借助 反向边来到2，再沿着2走到5，再走到6。

我们“借助”反向边，究竟干了什么？再回来看我们最开始选择的路径（1 -> 2 -> 4 -> 6），在2 -> 4的路径上，我们以流量5流过这条路。但是，这样的方案是一种错误的方案（见图，一个好的方案是在2 -> 4中流3的流量），因此，我们要修正这个错误，如何修正？那就是我们在搜索新路径的时候，尝试用现有的流量去冲击，或者说抵消 原本的流量。

具体来说，在这个例子里，原本从2->4的流量是5，我们现在有2的流量，我们尝试用2的流量去“抵消”，于是从2 -> 4的流量就变成了3；我们最大能抵消多少流量呢？我们最大能抵消的流量，自然就是我们上一步选择的方案中从2 -> 4的流量和我们现有的流量的最小值。

再换个角度，我们在2 -> 4上抵消了一部分流量，就相当于把一部分流量从4还给了2，因此，就相当于从2号点，我们就进行了分流！这样，我们就成功修正了错误。也因此，在算法中，我们就得到了一条虚拟的路径（1-> 3 -> 4 -> 2 -> 5 -> 6），但是实际上这样的路径是不存在的，我们只不过借助反向边，将错误路径进行修正。其实如果仔细观察会发现，最大流7的两条路径分别为：1 -> 3 -> 4 -> 6，1 -> 2，接着分流到4和5，再到6，而我们的错误做法在算法运行时会产生的路径为：1 -> 2 -> 4 -> 6和1-> 3 -> 4 -> 2 -> 5 -> 6，而当我们在错误处（2 -> 4）进行修正后，我们就把算法产生的路径，修改成了正确的路径，关于这一点，可以仔细思考，或者模拟一下。

反向边的权值是多少？

显然，反向边的存在，是为了消除错误的方案的选择，因此反向边的权值，就应当是上一步方案中，流过该边的流量。

因此，按照算法得到的最大流方案为什么也长成这个样子，就呼之欲出了，因为在2 -> 4的路径上，他反悔了。