学习笔记17--汽车运动控制理论之现代控制理论

本系列博客包括6个专栏，分别为：《自动驾驶技术概览》、《自动驾驶汽车平台技术基础》、《自动驾驶汽车定位技术》、《自动驾驶汽车环境感知》、《自动驾驶汽车决策与控制》、《自动驾驶系统设计及应用》。
此专栏是关于《自动驾驶汽车决策与控制》书籍的笔记.

---

---

1.汽车运动控制理论

1.2 现代控制理论

1.2.1 线性二次型最优控制

1. 基本内容

   • 线性二次型最优控制亦称线性二次型调节器(Linear Quadratic Regulator，LQR)，应用线性二次型最优控制原理设计的控制器；
   • 作用是当系统状态因为某种原因导致偏离了平衡点时，在不消耗多余能量的情况下，使系统状态仍然保持在平衡点附近；
   • 线性二次型最优控制的控制对象是具有线性或可线性化特点的，且性能指标是状态变量和控制变量的二次型函数的积分；
   • 典型LQR调节器结构如下图所示：

2. 无限时间状态的LQR调节器的设计过程

   设线性系统的状态空间描述为：
   { x ˙ ( t ) = A x ( t ) + B u ( t ) y = C x ( t ) (3) {˙x(t)=Ax(t)+Bu(t)y=Cx(t)

   \tag{3} {​x˙(t)=Ax(t)+Bu(t)y=Cx(t)​(3)
   最优控制的关键是如何求得一组反馈控制序列$u$，在时间段$[t_0,\infty ]$内，该控制序列作为控制系统的输入，可以将控制系统由非平衡状态调节到零点(平衡状态)附近，同时能够使性能指标函数的值最小；

   性能指标函数表示为$J$，有：
   $$J=\frac{1}{2}\sum _{-\infty }^{\infty }(x^{T}Qx+u^{T}Ru)dt\text{\hspace{1em}(4)}$$
   其中：$u$不受限制，$Q$是半正定对称加权常数矩阵，$R$是正定对称加权常数矩阵；

   一般来说，$Q$越大，系统达到稳态的时间越短，最优控制律为：
   $$u^{\ast }=-R^{-1}{B}^{T}Px\text{\hspace{1em}(5)}$$
   其中：$P$为正定对称常数矩阵，且满足下列Riccati方程：
   $$PA+A^{T}P-PB{R}^{-1}{B}^T+Q=0\text{\hspace{1em}(6)}$$
   利用MATLAB求解即可；

1.2.2 模糊控制

1. 基本内容

   • 模糊控制器(Fuzzy Controller，FC)亦称模糊逻辑控制器(Fuzzy Logic Controller，FLC)；
   • 模糊控制器使用的模糊控制规则，是由模糊集合论中的模糊条件语句构成；模糊控制器属于语言型控制器，常被称为模糊语言控制器(Fuzzy Language Controller，FLC)；
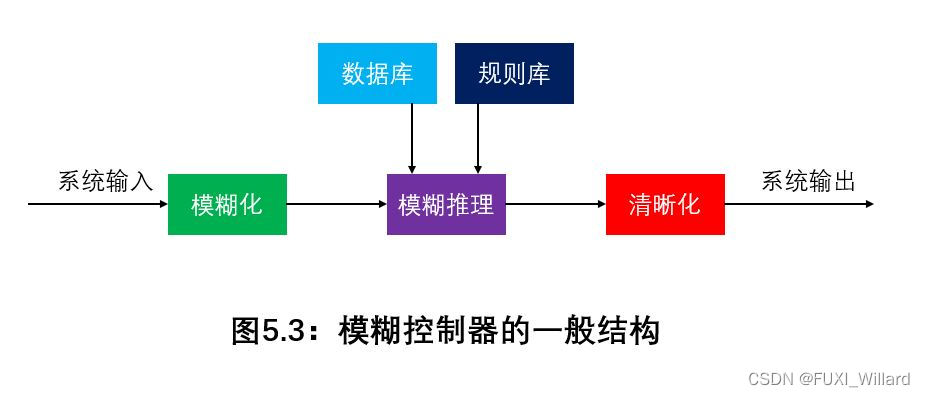
   • 模糊控制器的一般结构如下图所示：

2. 模糊控制器各主要环节的功能

   • 模糊化环节：将系统中的所有精确量(包括：系统的外界参考输入、系统输出和系统状态等)转换为模糊量，使其变成符合模糊控制器要求的输入量，然后进行尺度变换，把其变换到各自的论域范围内，再进行模糊化处理，使原来精确的输入量变为模糊量，并用相应的模糊集合表示；
   • 数据库和规则库环节：包含控制系统具体应用过程中的知识和控制要求，通常由专家数据库和模糊控制规则库组成；专家数据库包括变量的隶属函数、尺度变换因子和模糊空间的分级数等；模糊规则库包括用模糊变量表示的一系列控制规则，能够反映控制专家的经验和知识；
   • 模糊推理环节：能够模拟人基于模糊概念的推理过程，其推理过程是基于模糊逻辑中的蕴含关系和推理规则的；
   • 清晰化环节：将模糊推理过程所得的控制量转换为用于控制的清晰量，包含两个过程：第一，将模糊控制量经清晰化处理，先变换为表示在其论域范围内的清晰量；第二，将第一步得到的清晰量经过尺度变换，转换成实际的控制量；

1.2.3 自适应控制

1. 基本内容

   • 自适应控制系统需要不断地测量系统本身的状态、性能、参数，并对系统当前数据和期望数据进行比较，再做出改变控制器结构、参数或控制方法等的最优决策；
   • 系统不断测量输入和扰动，与参考输入对比，根据需要不断地调节自适应机构，既要保证系统输出满足要求，还要保证系统的稳定；

2. 自适应控制系统的设计过程

   设可控系统的受控对象数学模型为：
   { x ˙ p = A p x p + B p u p y p = C x p (7) {˙xp=Apxp+Bpupyp=Cxp

   \tag{7} {​x˙p​=Ap​xp​+Bp​up​yp​=Cxp​​(7)
   其中：$x_p$为状态向量，$u_p$为控制向量，$y_p$为输出向量，$A_p、B_p、C$分别为相同维数的系数矩阵；

   选定参考模型时，通常使其具有与被控对象相同的结构形式，参数根据系统设计要求确定，参考模型表示为：
   { x ˙ m = A m x m + B m r m y m = C x m (8) {˙xm=Amxm+Bmrmym=Cxm

   \tag{8} {​x˙m​=Am​xm​+Bm​rm​ym​=Cxm​​(8)
   其中：$x_m$为参考模型的状态向量，$y_m$为参考模型的输出向量，$r_m$为参考模型的输入向量，$A_m、B_m$分别是有相同维数的表示期望性能的系数矩阵；

   系统的广义输出误差方程为：
   $$\epsilon =y_m-y_p\text{\hspace{1em}(9)}$$
   其中：$y_m$为模型的输出量，$y_p$为可调系统的输出量；

   系统的广义状态误差方程为：
   $$e=x_m-x_p\text{\hspace{1em}(10)}$$
   广义误差运动方程为：
   $$\dot{e}(t)=A_{m}e+(A_m-A_p)x_p+B_m{r}_m-B_p{u}_p\text{\hspace{1em}(11)}$$
   自适应控制需要使等效误差的解$\epsilon$和$e$尽可能小；

1.2.4 模型预测控制

1. 基本内容
   • 模型预测控制(Model Predictive Control，MPC)，在每一个采样周期，通过求解一个有限时域开环最优控制问题来获得当前的控制序列；
   • 模型预测控制是一种与时间相关的、利用系统当前状态和当前的控制量，来实现对系统未来状态的控制；
   • 模型预测控制致力于将更长时间跨度甚至无穷时间的最优化控制问题，分解为若干更短时间跨度或有限时间跨度的最优化控制问题，且在一定程度上仍然追求最优解；本质上模型预测控制是要求解一个开环最优控制问题，思想与具体的模型无关，实现的过程与模型有关；
2. 模型预测控制的三个组成部分
   • 第一部分，预测模型；预测模型应该能够结合系统的现在的控制输入及过程的历史信息，来预测控制系统未来的输出值，因此，需要一个系统动态行为的模型作为预测模型；在预测控制中的各种不同算法中，常采用不同的预测模型，如：模型算法控制(Model Algorithm Control，MAC)，采用的是系统的单位脉冲响应曲线；动态矩阵控制(Dynamic Matrix Control，DMC)，采用的是系统的阶跃响应曲线；
   • 第二部分：反馈校正；利用预测模型进行预估系统的输出值，是一种理想情况；实际过程中，因为存在模型失配和干扰等不确定因素，使得基于模型预测结果不能与实际情况切合；需要在预测过程中，增加对系统输出值的测量，并与模型预估值进行比较，得出模型的预测误差，利用预测误差对模型的预测值作修正；预测控制是基于模型的，还增加了反馈控制，属于闭环优化控制；
   • 第三部分：滚动优化；预测控制需要通过某一性能指标的最优求解来确定未来的控制动作，这一性能指标与控制系统未来的行为有关，由未来的控制策略决定；优化过程不是单次离线完成的，而是多次在线进行的；在任意采样时刻，优化性能指标只应用在自该时刻起到未来的有限时间区间，当进行到下一采样时刻，该优化区间同时向前；

1.2.5 神经网络控制

• 神经网络控制：指应用神经网络技术，对控制系统中难以精确建模的复杂非线性对象进行神经网络模型辨识，可以作为控制器，可以对参数进行优化设计，可以进行推理，可以进行故障诊断；

• 通常神经网络直接作为误差闭环系统的反馈控制器，神经网络控制器先利用其已有的控制样本离线训练，后以系统误差的均方差为评价函数进行在线学习；

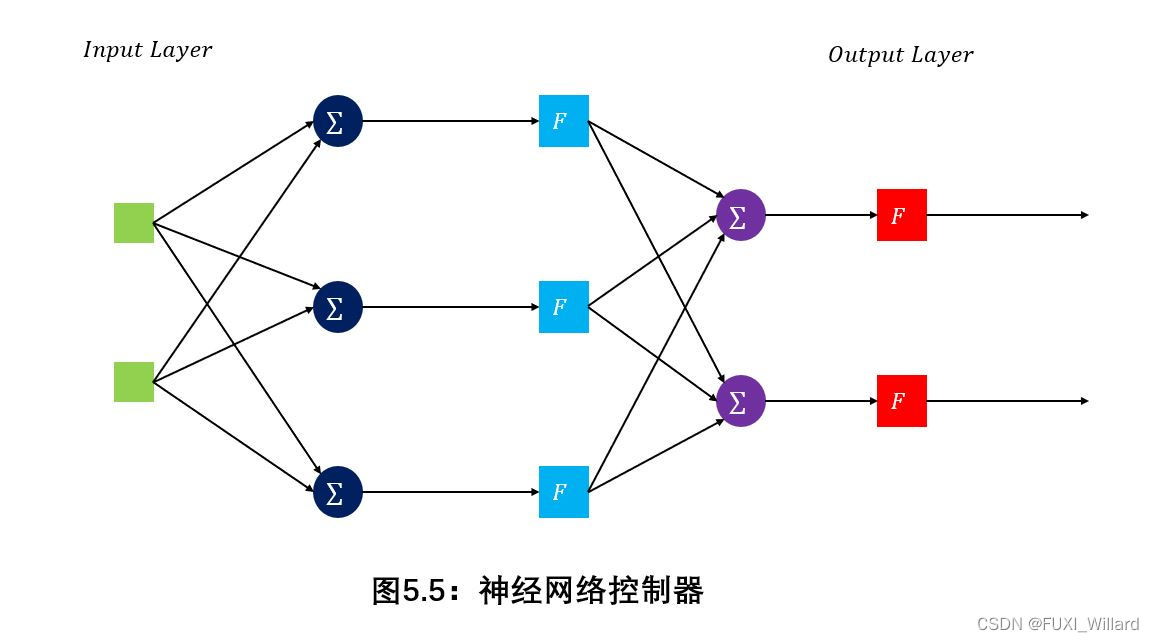
• 神经网络控制器如下图所示：
  

• 常见的神经网络控制结构：

  • 参数估计自适应控制系统；
  • 内模控制系统；
  • 预测控制系统；
  • 模型参考自适应系统；
  • 变结构控制系统；