• 有关栈和队列的三道OJ题【C语言】

    目录

    1.认识栈和队列

    概念

    栈和队列是两个逻辑不同的数据结构

    栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
    队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列遵循先进先出FIFO(First In First Out) 的原则。入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头

    🔎在C语言中，为了运用栈和队列来解决OJ题和实际问题，我们必须先自己写出来这两种数据结构才能用。因此我们先实现栈和队列，并用其来解决后面的问题。

    实现

    🌲栈的实现

    //Stack.h
//顺序表实现栈
#pragma once
#include 
#include 
#include 
#include 

#define InitCapacity 4 //栈的初始容量
#define MUL 2 //栈每次扩容的倍数

typedef int StackDataType;
typedef struct
{
	StackDataType* arr;//栈主体
	int top;//栈顶(实际上是栈顶元素的下一个位置)
	size_t capacity;//容量
}Stack;

void StackInit(Stack* pst);//栈的初始化
void StackDestroy(Stack* pst);//栈的销毁
void StackPrint(Stack* pst);//打印
bool StackIsEmpty(Stack* pst);//判断栈是否为空
void StackPush(Stack* pst, StackDataType data);//压栈
void StackPop(Stack* pst);//出栈
StackDataType StackTop(Stack* pst);//获取栈顶元素
size_t StackSize(Stack* pst);//获取栈中有效元素的个数

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    //Stack.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"

void CheckCapacity(Stack* pst)//检查并扩容
{
	assert(pst);
	if (pst->capacity == pst->top)
	{
		size_t newcapacity = (pst->capacity == 0 ? InitCapacity : MUL * pst->capacity);
		StackDataType* tmp = (StackDataType*)realloc(pst->arr, sizeof(StackDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		//
		pst->arr = tmp;
		pst->capacity = newcapacity;
	}
}

void StackInit(Stack* pst)//栈的初始化
{
	assert(pst);
	pst->capacity = pst->top = 0;
	pst->arr = NULL;
}

void StackDestroy(Stack* pst)//栈的销毁
{
	assert(pst);
	//
	free(pst->arr);
	pst->arr = NULL;
	//
	pst->capacity = pst->top = 0;
}

void StackPrint(Stack* pst)//打印
{
	assert(pst);
	//
	if (StackIsEmpty(pst))
	{
		printf("NULL\n");
	}
	//
	for (int i = 0;i < pst->top;i++)
	{
		printf("%d ", pst->arr[i]);
	}
	printf("\n");
}

bool StackIsEmpty(Stack* pst)//判断栈是否为空
{
	assert(pst);
	//
	return pst->top == 0;
}

void StackPush(Stack* pst, StackDataType data)//压栈
{
	assert(pst);
	//
	CheckCapacity(pst);//检查容量
	//
	pst->arr[pst->top] = data;
	pst->top++;
}

void StackPop(Stack* pst)//出栈
{
	assert(pst);
	assert(!StackIsEmpty(pst));//判断栈是否为空，为空则无法出栈
	//
	pst->top--;
}

StackDataType StackTop(Stack* pst)//获取栈顶元素
{
	assert(pst);
	assert(!StackIsEmpty(pst));
	//
	return pst->arr[pst->top - 1];
}

size_t StackSize(Stack* pst)//获取栈中有效元素的个数
{
	assert(pst);
	return pst->top;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93

    🌲队列的实现

    //Queue.h
//链表实现队列
#pragma once
#include 
#include 
#include 
#include 

typedef int QueueDataType;
//队列的结点
typedef struct QueueNode
{
	QueueDataType data;
	struct QueueNode* next;
}QueueNode;

typedef struct
{
	QueueNode* front;//队头指针
	QueueNode* rear;//队尾指针
	int size;//队列的长度
}Queue;

void QueueInit(Queue* pqe);//队列初始化
void QueueDestroy(Queue* pqe);//队列销毁
void QueuePrint(Queue* pqe);//打印队列
bool QueueIsEmpty(Queue* pqe);//判断队列是否为空
void QueuePush(Queue* pqe, QueueDataType data);//队尾入元素
void QueuePop(Queue* pqe);//队头出元素
QueueDataType QueueFront(Queue* pqe);//获取队头元素
QueueDataType QueueRear(Queue* pqe);//获取队尾元素
int QueueSize(Queue* pqe);//获取队列中有效元素个数

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    //Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"

void QueueInit(Queue* pqe)//队列初始化
{
	assert(pqe);
	//
	pqe->front = pqe->rear = NULL;
	pqe->size = 0;
}

void QueueDestroy(Queue* pqe)//队列销毁
{
	assert(pqe);
	//
	QueueNode* cur = pqe->front;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	//
	pqe->front = pqe->rear = NULL;
}

void QueuePrint(Queue* pqe)//打印队列
{
	assert(pqe);
	//
	QueueNode* cur = pqe->front;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}

bool QueueIsEmpty(Queue* pqe)//判断队列是否为空
{
	assert(pqe);
	//
	return pqe->front == NULL && pqe->rear == NULL;
}

void QueuePush(Queue* pqe, QueueDataType data)//队尾入元素
{
	assert(pqe);
	//创建新结点
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->data = data;
	newnode->next = NULL;
	//链接
	if (pqe->front == NULL)
	{
		pqe->front = pqe->rear = newnode;
	}
	else
	{
		pqe->rear->next = newnode;
		pqe->rear = pqe->rear->next;
	}
	//
	pqe->size++;
}

void QueuePop(Queue* pqe)//队头出元素
{
	assert(pqe);
	assert(!QueueIsEmpty(pqe));
	//出列
	QueueNode* next = pqe->front->next;
	free(pqe->front);
	pqe->front = next;
	//如果删的是最后一个，删完front会变为NULL，此时rear也应该置为NULL
	if (pqe->front == NULL)
	{
		pqe->rear = NULL;
	}
	//
	pqe->size--;
}

QueueDataType QueueFront(Queue* pqe)//获取队头元素
{
	assert(pqe);
	assert(!QueueIsEmpty(pqe));
	//
	return pqe->front->data;
}

QueueDataType QueueRear(Queue* pqe)//获取队尾元素
{
	assert(pqe);
	assert(!QueueIsEmpty(pqe));
	//
	return pqe->rear->data;
}

int QueueSize(Queue* pqe)//获取队列中有效元素个数
{
	assert(pqe);
	return pqe->size;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111

    2.用队列实现栈

    🍉题目

    在这里插入图片描述

    🍎思路

    🎈用两个队列实现后入先出的栈，我们的结构大概是这样的：
    在这里插入图片描述
    🎈因为栈的后入先出的特点和队列的先入先出的特点大不相同，因此我们在Pop（出栈）之前需要将先入的数据挪到另外一个队列。就像这样
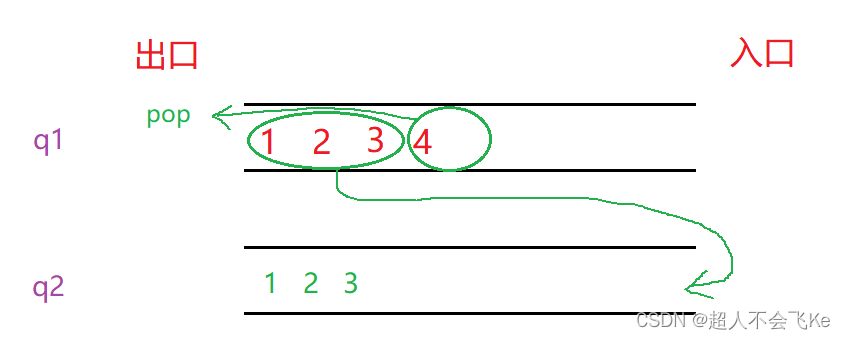
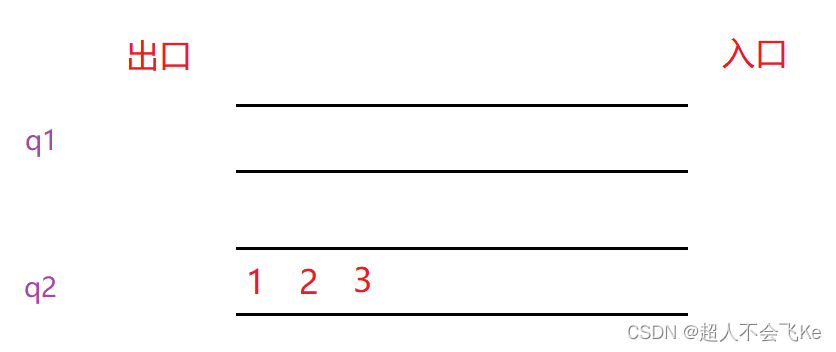
    在这里插入图片描述
    在这里插入图片描述

    因为4是后进入的数据，在栈的角度看它是栈顶，出栈时需要出的数据便是栈顶4。
    另外需要注意的是，我们要保证至少有一个队列为空，在出栈挪动数据时将非空队列的所有数据挪动到空队列中。否则，会混乱模拟栈的顺序。

    ⭕综上所述，我们用队列模拟栈是这样实现的
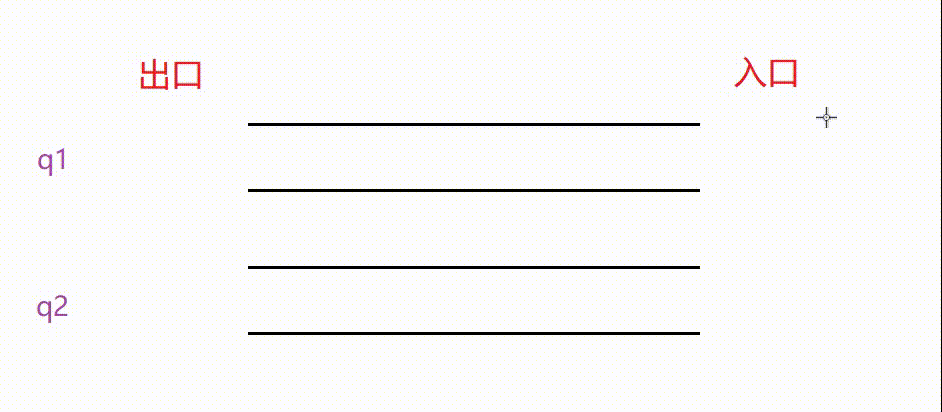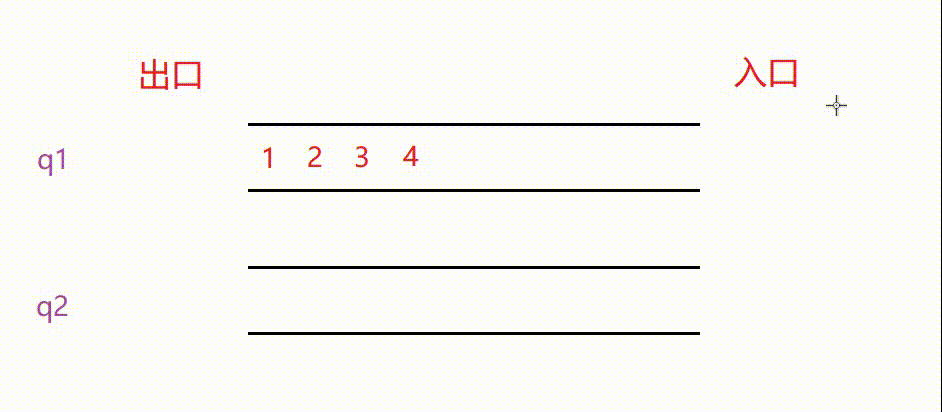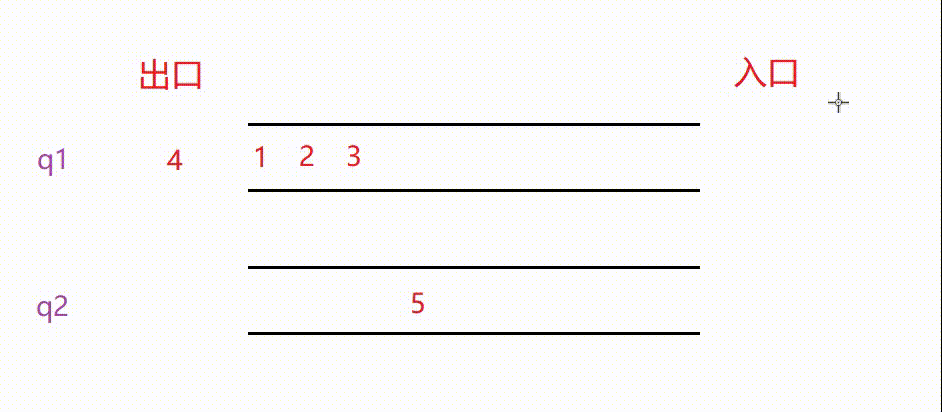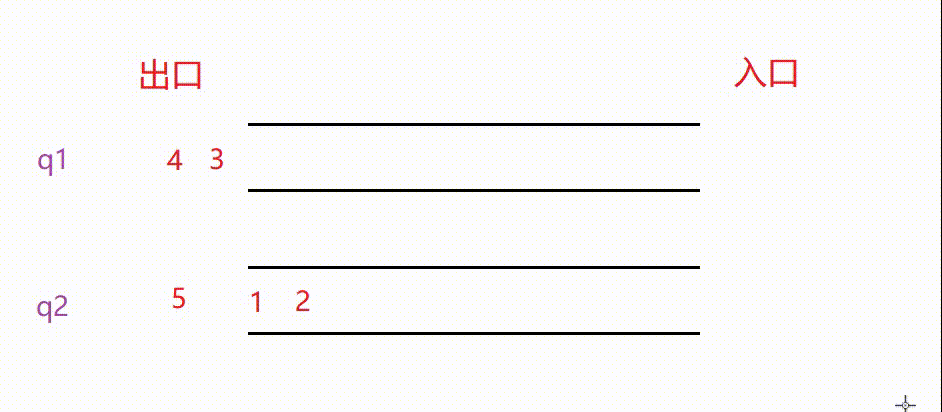
    在这里插入图片描述

    从图中可以清晰地看到：
    入栈：当两个队列皆为空时，我们可以选取任意的队列入数据。当两个队列一个为空一个不为空时，我们要选择不为空的队列入数据。
    出栈： 每次出栈，我们关注不为空的队列，该队列的队尾既为模拟栈的栈顶。要想弹出这个队尾的数据，应该先将队尾前面的所有数据挪动到另外一个空队列，这样队尾便成了队头，直接从队头出数据即可。
    取栈顶和判空： 而取栈顶元素就是取不为空的队列的队尾元素，判断栈是否为空只需要判断两个队列是否都为空即可，这两个接口相对容易实现。

    🍑实现

    //引用第一目我们实现的队列以及各种接口
//模拟栈的结构（由两个队列构成）
typedef struct {
    Queue q1;
    Queue q2;
} MyStack;

//创建一个模拟栈
MyStack* myStackCreate() {
    MyStack* tmp = (MyStack*)malloc(sizeof(MyStack));
    if(tmp == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
    //
    QueueInit(&tmp->q1);
    QueueInit(&tmp->q2);
    return tmp;
}

//入栈,找到不为空的队列
void myStackPush(MyStack* obj, int x) {
    assert(obj);
    if(QueueIsEmpty(&obj->q1))//q1空q2不空 或 q1q2都空
    {
        QueuePush(&obj->q2,x);
    }
    else//q1不空q2空
    {
        QueuePush(&obj->q1,x);
    }
}

//出栈，要挪动数据
int myStackPop(MyStack* obj) {
    assert(obj);
    //找出空队列和非空队列(先默认q1为空q2为非空，再纠错)
    Queue* empty = &obj->q1;
    Queue* nonempty = &obj->q2;
    if(!QueueIsEmpty(&obj->q1))
    {
        empty = &obj->q2;
        nonempty = &obj->q1;
    }
    //挪动非空队列的数据到空队列,留下队尾
    while(QueueSize(nonempty)>1)
    {
        QueuePush(empty,QueueFront(nonempty));
        QueuePop(nonempty);
    }
    int ret = QueueFront(nonempty);
    QueuePop(nonempty);
    return ret;
}

//取栈顶元素
int myStackTop(MyStack* obj) {
    assert(obj);
    Queue* empty = &obj->q1;
    Queue* nonempty = &obj->q2;
    if(!QueueIsEmpty(&obj->q1))
    {
        empty = &obj->q2;
        nonempty = &obj->q1;
    }
    //
    return QueueRear(nonempty);
}

//判空
bool myStackEmpty(MyStack* obj) {
    assert(obj);
    return QueueIsEmpty(&obj->q1) && QueueIsEmpty(&obj->q2);
}

//释放空间
void myStackFree(MyStack* obj) {
    assert(obj);
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83

    3.用栈实现队列

    🍉题目

    在这里插入图片描述

    🍎原理

    🎈用栈模拟实现队列的结构是这样的，两个栈，一个用于入数据，一个用于出数据。
    在这里插入图片描述

    由于栈先入后出的特性，我们将pushST中的数据挪到popST中后，数据的顺序恰好会发生改变，这时先前的栈底（pushST的栈底）会变成栈顶（pushST的栈顶），这个栈顶就是模拟队列的队头，此时便可以通过popST出去。

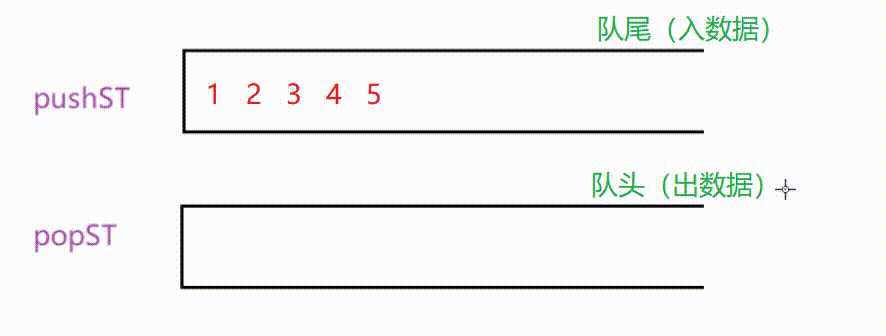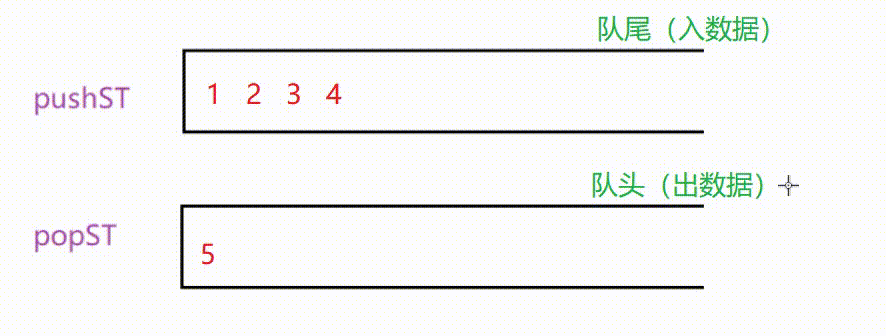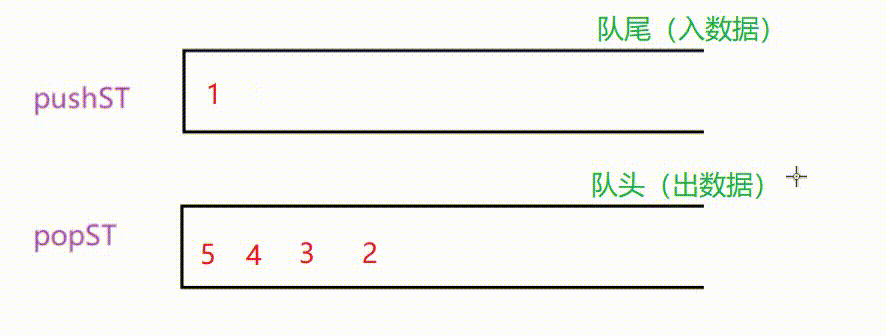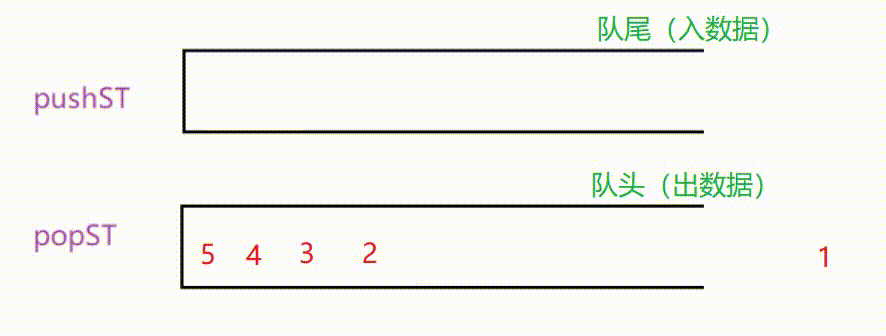
    在这里插入图片描述

    🎈需要注意的是，每次我们要pop数据时，要检查popST中是否有数据。如果有就直接pop其中的数据，如果没有才需要将pushST中的数据挪动过来。否则也会导致队列的顺序混乱

    ⭕如下图：
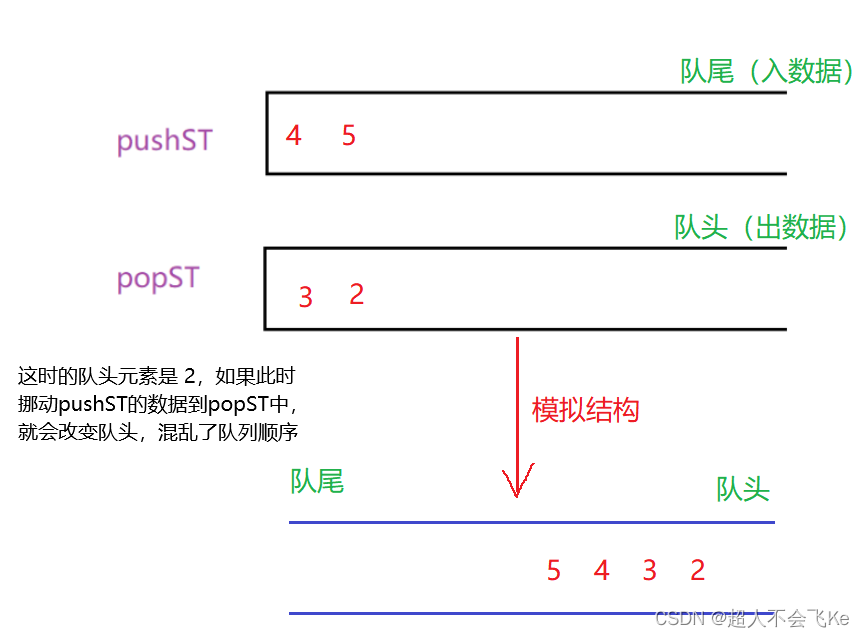
    在这里插入图片描述

    🍑实现

    typedef struct {
    Stack pushST;
    Stack popST;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* tmp = (MyQueue*)malloc(sizeof(MyQueue));
    if(tmp == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
    //
    StackInit(&tmp->pushST);
    StackInit(&tmp->popST);
    //
    return tmp;
}

bool myQueueEmpty(MyQueue* obj) {
    assert(obj);
    return StackIsEmpty(&obj->pushST) && StackIsEmpty(&obj->popST);
}

void myQueuePush(MyQueue* obj, int x) {
    assert(obj);
    StackPush(&obj->pushST,x);
}

int myQueuePop(MyQueue* obj) {
    assert(obj);
    //如果popST为空，则将pushST中所有元素转移到popST中
    if(StackIsEmpty(&obj->popST))
    {
            while(!StackIsEmpty(&obj->pushST))
            {
                StackPush(&obj->popST,StackTop(&obj->pushST));
                StackPop(&obj->pushST);
            }
    }
    //popST出栈
    int ret = StackTop(&obj->popST);
    StackPop(&obj->popST);
    return ret;
}

int myQueuePeek(MyQueue* obj) {
    assert(obj);
    assert(!myQueueEmpty(obj));//控制队列不为空，才能取队头
    if(!StackIsEmpty(&obj->popST))
    {
        return StackTop(&obj->popST);
    }
    else
    {
        while(!StackIsEmpty(&obj->pushST))
        {
            StackPush(&obj->popST,StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
        return StackTop(&obj->popST);
    }
}

void myQueueFree(MyQueue* obj) {
    assert(obj);
    StackDestroy(&obj->pushST);
    StackDestroy(&obj->popST);
    free(obj);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71

    4.设计循环队列

    🍉题目

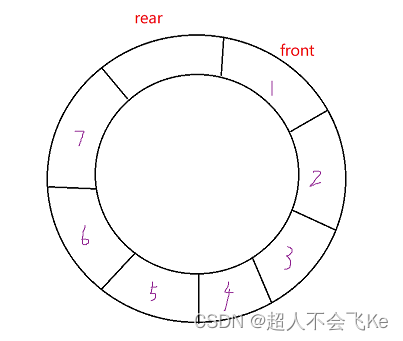
    在这里插入图片描述

    🍎思路

    在这里插入图片描述

    💡循环队列的逻辑结构是这样的：队头与队尾相连接，并用front和rear两个指针分别控制队头和队尾，front和rear之间的空间为循环队列的有效空间。出入数据时，空间可以重复利用，提高的空间的使用率。

    ⭕这里其实用链表和数组（顺序表）都能实现循环队列，但是考虑到rear是队尾元素的下一个位置，使用单链表无法访问到队尾元素。为了结构的简洁性，这里我们用顺序表实现循环队列。

    假设我们要设计一个长度为5的队列，那按正常思路我们开辟一个长度为5的数组应该是能够解决问题的，但当我们实际操作时，会遇到以下问题。
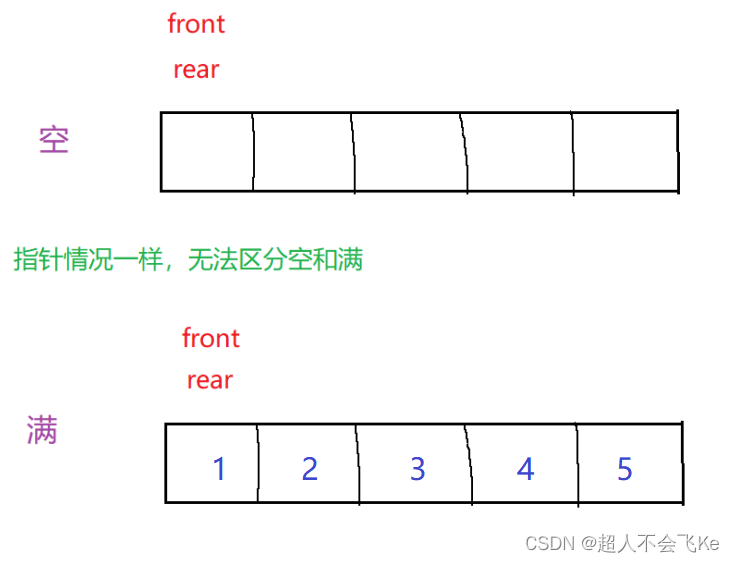
    在这里插入图片描述

    ⭕无法区分队列的空和满该如何解决呢？有两种思路：
    1.多开辟一个空间，这个空间不存储数据
    2.利用变量Size记录队列的有效长度

    我们用第一种思路，也是比较常见的一种思路，解决如下：
    在这里插入图片描述

    🎈我们可以看到，现在无论是哪种情况的满，rear的下一个位置是front，很好区分空和满，而且rear指向的空间永远没有值，这个空间是为了区分队列空和满而开辟的。

    🔎我们还需要注意一种情况，当front和rear在队中时，移动时只需要+1即可。那么，如果他们在队尾应该怎么移动呢？根据循环队列的逻辑结构，我们知道当rear(或front)在队尾时，移动到下一个位置肯定是下标为0的位置，直接+1可能就越界了。粗暴一点解决就是直接加一个判断条件，如果rear(或front)在队尾便归回0。而巧妙运用一点数学，你会发现这其实非常简单。
    假设队列的长度为N(有效长度为N-1)，那么在往后移动rear(或front)的时候，我们有一个公式：
    rear = (rear+1)%N - - - (移动front就把rear换成front)

    同理，在往前移动rear(或front)的时候，也有一个公式：
    rear = (rear-1+N)%N - - - (移动front就把rear换成front)

    这是一个通式，不管rear(或front)在队中还是队尾，都能正确的移动以达成我们想要的结果。

    🔎相同道理，若要计算循环队列的有效长度Len，也有一个公式：
    Len = (rear-front+N)%N

    这个公式无论rear和front谁大谁小都是适用的
    %N：确保了rear>front情况的准确性，可理解为此时rear-front是 有效长度
    +N：确保了rear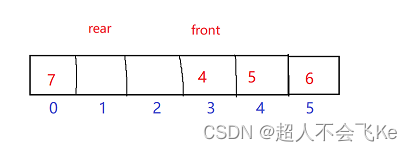

    在这里插入图片描述
    例如这种情况，(rear-front+N)%N = (1-3+6)%6 = 4
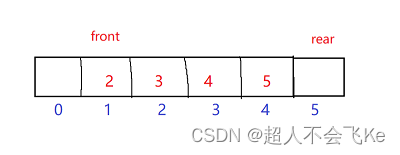
    在这里插入图片描述
    又如这种情况，(rear-front+N)%N = (5-1+6)%6 = 4

    🍑实现

    typedef struct {
    int* a;
    int front;
    int rear;
    int N;//队列的长度
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    int* pa = (int*)malloc(sizeof(int)*(k+1));
    //
    obj->a = pa;
    obj->front = obj->rear = 0;
    obj->N = k+1;//多开一块空间，用于判空满
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    assert(obj);
    return obj->front == obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    assert(obj);
    return obj->front == (obj->rear+1) % (obj->N);//运用公式，算得上rear的下一个位置的下标值
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    assert(obj);
    if(!myCircularQueueIsFull(obj))
    {
        obj->a[obj->rear] = value;
        obj->rear = (obj->rear+1) % (obj->N);//运用公式
        return true;
    }
    return false;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    assert(obj);
    if(!myCircularQueueIsEmpty(obj))
    {
        obj->front = (obj->front+1) % (obj->N);//运用公式
        return true;
    }
    return false;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    assert(obj);
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    {
        return obj->a[obj->front];
    }
}

int myCircularQueueRear(MyCircularQueue* obj) {
    assert(obj);
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    {
        return obj->a[(obj->rear-1+obj->N)% obj->N];//运用公式
    }
}

void myCircularQueueFree(MyCircularQueue* obj) {
    assert(obj);
    free(obj->a);
    obj->a = NULL;
    free(obj);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79

    🌝Good Night

  • 相关阅读:
    MYSQL CONCAT函数
    day22集合01
    使用fastapi和pulumi搭建基于Azure云的IAC Restful API服务 — 对外发布
    java-常用正则操作
    随笔-服务器运维常用的命令
    QML绘图系统
    具有计算功能的模拟信号平均值采集隔离放大器
    [发送AT指令配置a7670C模块上网]
    Leetcode739. 每日温度
    基于Python实现种差值方法
  • 原文地址：https://blog.csdn.net/C0631xjn_/article/details/126273083