活动地址：CSDN21天学习挑战赛

📚“九层之台，起于垒土”。学习技术须脚踏实地。

☀️你要做冲出的黑马，而不是坠落的星星。
📖这里推荐一款刷题、模拟面试神器，可助你斩获心仪大厂offer：点我免费刷题、模拟面试

折半查找的概念

现代计算机和网络使我们能够访问海量的信息。高效 查找（检索） 这些信息的能力是处理它们的重要前提。

最简单的查找就是顺序查找，顺序查找就是对数据结构进行线性扫描，来查找满足要求的元素。

虽然顺序查找比较简单，但是它的时间复杂度是$O(n)$。如果元素是在有序的前提下继续使用顺序查找就会显得得不偿失了，因为还有一种折半查找的算法专一应用于有序序列。

折半查找： 也叫二分查找，每次搜索都会将搜索的目标区间缩小一半，所以可以保证在$O(lo{g}_{2}n)$的时间复杂度内完成查找。

1、折半查找

1.1 算法流程

• 输入

  • n 个数的有序序列 a，默认升序；
  • 待查找元素key。

• 开始查找，每次循环确定待查找区间的中点索引 mid，将 key 与 a[mid] 进行比较。

  • 若 key 与 a[mid] 相等：直接返回 mid；
  • 若 key 大于 a[mid]：待查找区间变为当前查找区间的左侧半区间；
  • 若 key 小于 a[mid]：待查找区间变为当前查找区间的右侧侧半区间。

• 如果查找过程中未返回 mid，则查找失败，返回 -1。

过程演示：

要查找的 key = 19


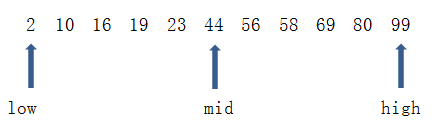
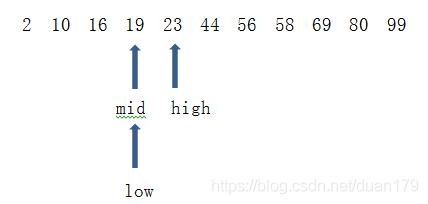
图片来源

1.2 C++实现

template<typename T>
int BinarySearch(T* a, int size, T key){
    int lo = 0, hi = size - 1;
    while(lo <= hi){
        int mid = lo + (hi - lo) / 2;
        if(key < a[mid]) hi = mid - 1;
        else if(key > a[mid]) lo = mid + 1;
        else return mid;
    }
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11

循环控制条件解释：当lo = hi时，此处的元素还未与key进行比较，所以要设为 <=。

2、查找元素第一次与最后一次出现的位置

2.1 改进部分

首次出现：

• hi = mid找到下标时不返回，存入 hi， 逐步收缩右边界，找不到时则按照一般二分计算。

• 循环结束条件。

  退出前一步可能 mid = lo 或mid = (hi - lo) / 2 。

  mid = (hi - lo) / 2 时：

  • 如果 a[mid] = key，hi = mid，也就是下一种情况（mid = lo ）。
  • 如果 a[mid] < key，lo = hi，退出循环。
    
    

  mid = lo 时：

  • 如果 a[mid] = key，hi = mid = lo，退出循环。
  • 如果 a[mid] < key，lo = hi，退出循环。
  
  综上，退出循环时总有 `lo = hi`，所以，循环结束条件如果设置成 <= 将会无限循环。

• 循环退出时还未判断 hi 处的值，所以 if (a[hi] == key)用来判断上面循环未判断的 hi 处的值是否等于 key。因为 lo = hi 所以此处也可换为 if (a[lo] == key)。

最后出现：

• 利用**对称性（便于理解），类比上面的算法，很容易想到将else hi = mid;换成else lo = mid;，将下标存入 lo，收缩左边界。

• 但此时有一点不对称，就是计算 mid 时是取整计算，去掉小数点后的数，如果要对称的话就要在原始 mid 的基础上加 1。即 int mid = lo + (hi - lo) / 2 + 1;

2.2 C++实现

template<typename T>
int left(T* a, int size, T key) {
        int lo = 0;
        int hi = size - 1;
        while (lo < hi) {
            int mid = lo + (hi - lo) / 2;
            if (key < a[mid]) hi = mid - 1;
            else if (key > a[mid]) lo = mid + 1;
            else hi = mid;
        }
        if (a[hi] == key) 
            return hi;
        return -1;
    }
    
template<typename T>
int right(T* a, int size, T key) {
        int lo = 0;
        int hi = size - 1;
        while (lo < hi) {
            int mid = lo + (hi - lo) / 2 + 1;
            if (key < a[mid]) hi = mid - 1;
            else if (key > a[mid]) lo = mid + 1;
            else lo = mid;
        }
        if (a[lo] == key) //或 hi
            return lo;
        return -1;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3、复杂度分析

1. 时间复杂度：每次循环将查找范围缩小一半，所以时间复杂度为O(n)。
2. 空间复杂度：只需要维护一个索引变量，所以为O(1)。