一、二进制（机器数）

各种数值在计算机中表示的形式称为机器数，其特点是采用二进制计数制，数的符号用0和1表示，小数点则隐含，表示不占位置。机器数对于的实际数值称为数的真值，例如：

机器数： 1010
真值： 10
1
2

机器数有无符号和有符号之分，无符号数表示正数，在机器数中没有符号位；对于无符号数：

• 若约定小数点的位置在机器数的最低位之后，则是纯整数；
• 若约定小数点的位置在机器数的最高位之前，则是纯小数；

对于有符号数，机器数的最高位表示正、负的符号位（0为正，1为负），其余位则表示数值，例如：

机器数：1010
有符号数真值：-2
无符号数真值：10
1
2
3

十进制转二进制计算

• 整数
  

• 小数
  

---

二、原码、反码、补码和移码

码制：为了便于运算，带符号的机器数可采用原码、反码和补码等不同的编码方法；

2.1 原码表示法

数值X的原码记为[X]_原，如果机器字长为n（即采用n个二进制位表述数据），则原码的定义如下：

• 若X是纯整数
  
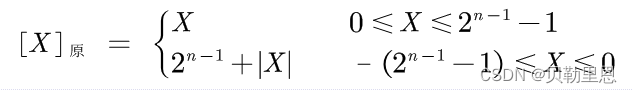
• 若X是纯小数
  

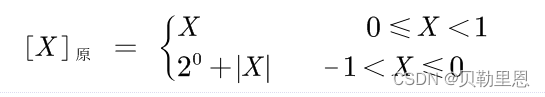
例如：若机器字长等于8,分别给出+1、-1，+127、-127、+45、-45、+0.5、-0.5的原码表示
1

[+1]_原 = 0 0000001
[-1]_原 = 1 0000001
[+127]_原 = 0 1111111
[-127]_原 = 1 1111111
[+45]_原 = 0 0101101
[-45]_原 = 1 0101101
[+0.5]_原 = 0 ◇1000000 注：◇是小数点的位置
[-0.5]_原 = 1 ◇1000000

在原码表示法中，最高位是符号位，0表示正号，1表示负号，其余的n-1位表示数值的绝对值。
数值0的原码表示有两种形式：[+0]_原 = 0 0000000，[-0]_原 = 1 0000000

---

2.2 反码表示法

数值X的反码记作[X]_反，如果机器字长为n，则反码的定义如下：

• 若X是纯整数
  
• 若X是纯小数
  

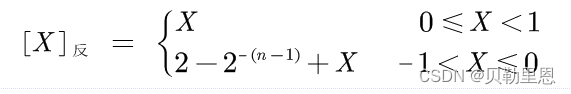
例如：若机器字长等于8,分别给出+1、-1，+127、-127、+45、-45、+0.5、-0.5的反码表示
1

[+1]_反 = 0 0000001
[-1]_反 = 1 1111110
[+127]_反 = 0 1111111
[-127]_反 = 1 0000000
[+45]_反 = 0 0101101
[-45]_反 = 1 1010010
[+0.5]_反 = 0 ◇1000000 注：◇是小数点的位置
[-0.5]_反 = 1 ◇0111111

在反码表示中，最高位是符号位，0表示正号，1表示负号，正数的反码和原码相同，负数的反码则是其绝对值按位求反。
数值0的反码表示有两种形式：[+0]_反 = 0 0000000，[-0]_反 = 1 1111111

---

2.3 补码表示法

数值X的补码记作[X]_补，如果机器字长为n，则补码的定义如下：

• 若X是纯整数
  
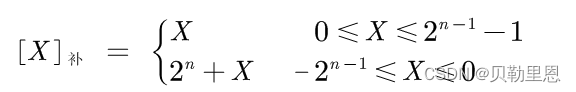
• 若X是纯小数
  

例如：若机器字长等于8,分别给出+1、-1，+127、-127、+45、-45、+0.5、-0.5的补码表示
1

[+1]_补 = 0 0000001
[-1]_补 = 1 1111111
[+127]_补 = 0 1111111
[-127]_补 = 1 0000001
[+45]_补 = 0 0101101
[-45]_补 = 1 1010011
[+0.5]_补 = 0 ◇1000000 注：◇是小数点的位置
[-0.5]_补 = 1 ◇1000000

在补码表示中，最高位为符号位，0表示正号，1表示负号，正数的补码与其原码和反码相同，负数的补码则在其反码的末位加1。
数值0的补码有唯一的编码：[+0]_补 = 0 0000000，[-0]_补 = 00000000

---

2.4 移码表示法

移码表示法是在数X上增加一个偏移量来定义的，常用于表示浮点数中的阶码。如果机器字长为n，规定偏移量为2^n-1，则移码的定义如下：

• 若X是纯整数
  
• 若X是纯小数
  

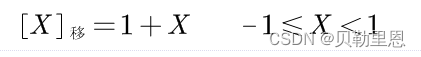
例如：若机器字长等于8,分别给出+1、-1，+127、-127、+45、-45、+0.5、-0.5的补码表示
1

[+1]_移 = 1 0000001
[-1]_移 = 0 1111111
[+127]_移 = 1 1111111
[-127]_移 = 0 0000001
[+45]_移 = 1 0101101
[-45]_移 = 0 1010011
[+0.5]_移 = 1 ◇0000000 注：◇是小数点的位置
[-0.5]_移 = 10000000

实际上，在偏移2^n-1的情况下，只要将补码的符号位取反便可获得相应的移码表示。

---

三、定点数和浮点数

3.1 定点数

所谓定点数，就是小数点的位置固定不变的数。小数点的位置通常有两种约定方式：定点整数（纯整数，小数点在最低有效数值位之后）和定点小数（纯小数，小数点在最高有效数值位之前）。
设机器字长为n，各种码制下带负号数的范围如下表所示：

---

3.2 浮点数

当机器字长为n时，定点数的补码和移码可表示2ⁿ个数，而其原码和反码只能表示2ⁿ-1个数（0的表示占用了两个编码），因此，定点数所能表示的数值范围比较小，在运算中很容易超出范围而溢出。浮点数是小数点位置不固定的数，它能表示更大范围的数。

在十进制中，一个数可以写成多种表示形式，例如，83.125可以写成10³x0.083125或10⁴x0.0083125等；
同样，一个二进制数也可以写成多种表示形式，例如，二进制数1011.10101可以写成2⁴x0.101110101、2⁵x0.0101110101或2⁶x0.00101110101等；
由此可知，一个二进制数N可以表示为更一般的形式：N=2^ExF（其中E称为阶码，F称为尾数），用阶码和尾数表示的数称为浮点数，这种表示数的方法称为浮点表示法。

在浮点表示法中，阶码为带符号的纯整数，尾数为带符号的纯小数，浮点数的表示格式如下：

很明显，一个数的浮点表示不是唯一的。当小数点的位置改变时，阶码也随着相应改变，因此可以用多个浮点形式表示一个数。

浮点数所能表示的数值范围主要由阶码决定，所表示数值的精度则由尾数决定。为了充分利用尾数来表示更多的有效数字，通常采用规格化浮点数。规格化就是将尾数的绝对值限定在区间[0.5,1]；

当尾数用补码表示时，需要注意：

• 若尾数M>=0，则其规格化的尾数形式为M=0.1 XXX…X，其中，X可为0，也可为1，即将尾数限定在区间[0.5,1]；
• 若尾数M<0，则其规格化的尾数形式为M=1.0XXX…X，其中，X可为0，也可为1，即将尾数限定在区间[-1,-0.5]；

如果浮点数的阶码（包括1位阶符）用R位的移码表示，尾数（包括1位数符）用M位的补码表示，则这种浮点数所能表示的数值范围如下：

• 最大的正数
  
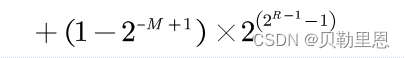
• 最小的负数
  

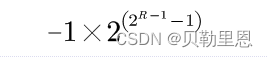
3.3 工业标准IEEE 754

IEEE 754是由IEEE制定的有关浮点数的工业标准，被广泛采用，该标准的表示形式如下：

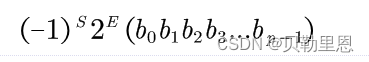
其中，

• (-1)^S为该浮点数的数符，当S为0时表示正数，当S为1时表示负数；
• E为指数（阶码），用移码表示；
• (b₀b₁b₂b₃…b_p-1)为尾数，其长度为p位，用原码表示；

目前，计算机中主要使用3种形式的IEEE 754浮点数，如下表所示：

根据IEEE 754标准，被编码的值分为3种不同的情况：规格化的值、非规格化的值和特殊值，规格化的值为最普遍的情形；

① 规格化的值
当阶码部分的二进制值不全为0也不全为1时，所表示的是规格化的值。例如，在单精度浮点格式下，阶码为10110011时，偏移量为+127（01111111），则其表示的真值为：10110011-01111111=00110100，转换为十进制后为52。
对于尾数部分，由于越大小数点左边隐含有一位，通常这位数就是1，因此单精度浮点数尾数的有效位数为24位，即尾数为1.xx…x，也就是说，不溢出的情况下，尾数M的值在1<=M<2之中，这是一种获得一个额外精度位的表示技巧。
例如：单精度浮点数格式下，b₀b₁…b₂₂ = 0100 1001 1000 1000 1001 011时，其对应的尾数真值为1+2^-2+2^-5+2^-8+2^-9+2^-13+2^-17+2^-20+2^-22+2^-23，即尾数的真值为1.28724038600921630859375（在程序中以十进制方式输出时，由于精度的原因不能完全给出此值）。

例：利用IEEE 754标准将数176.0625表示为单精度浮点数
1

解：

• 1、首先将该十进制转换成二进制数：
  (176.0625)₁₀ = (10110000.0001)₂
• 2、对二进制数进行规格化处理：
  10110000.0001 = 1 ◇ 01100000001x2⁷
  这就保证了使b₀为1，而且小数点应当在◇位置上。
• 3、将b₀去掉并扩展为单精度浮点数所规定的23位尾数
  01100000001 --> 01100000001000000000000
• 4、求阶码，上述表示中的指数为7，而单精度浮点数规定指数的偏移量为127（注意：不是前面移码描述中所提到的128），即在指数7上加127，那么E=7+127=134，则指数的移码表示为10000110
• 5、最后，可得到(176.0625)₁₀的单精度浮点数表示形式：
  0 10000110 01100000001000000000000

---

② 非规格化的值
当阶码部分的二进制值全为0时，所表示的数是非规格化的。在这种情况下，指数的真值为1-偏移量（对于单精度浮点数为-126，双精度浮点数为-1022），尾数的值就是二进制形式对应的小孙，不包含隐含的1。

非规格化数有两个用途，一是用来表示数值0，二是表示那些非常接近于0的数。因为在规格化表示方式下，必须使尾数大于等于1，因此不能表示出0.实际上，+0.0的浮点表示时符号、阶码和尾数的二进制表示都全为0.需要注意的是，符号位为1而阶码和尾数部分全为0时表示-0.0，也就是说，+0.0和-0.1在浮点表示时有所不同。

---

③ 特殊值
当阶码部分的二进制值全为1时，表示特殊值。当尾数部分全部为0时表示无穷大，，符号位为0时表示+∞，符号位为1是表示-∞；当浮点运算溢出时，用无穷来表示；当尾数部分不全为0时，称为“NaN”，即“不是一个数”。当运算结果不是实数或者无穷，就表示为NaN。

---

3.4 浮点数的运算

设有浮点数X = Mx2ⁱ，Y = Nx2^j，求X+Y（X-Y）的运算过程要经过对阶、求尾数和（差）、结果规格化并判移除、舍入处理和溢出判断等步骤。

• 对阶：使两个数的阶码相同。令K=|i-j|，把阶码小的数的尾数右移K位，使其阶码加上K；
• 求尾数和（差）；
• 结果规格化并判溢出：若运算结果所得的尾数不是规格化的数，则需要进行规格化处理。若尾数溢出时，需要调整阶码；
• 舍入处理：在对结果右规时，尾数的最低位将因移出而丢掉。另外，在对阶过程中也会将尾数右移使最低位丢掉，这就需要进行舍入处理，以求得最小的运算误差；
• 溢出判别：以阶码为准，若阶码溢出，则运算结果溢出；若阶码下溢（小于最小值），则结果为0；否则结果正确，无溢出；

浮点数相乘，其积的阶码等于两乘数的阶码相加，积的尾数等于两乘数的尾数相乘。

浮点数相除，其商的阶码等于被除数的阶码减去除数的阶码，商的尾数等于被除数的尾数除以除数的尾数。

注意：乘除运算的结果都需要进行规格化处理并判断阶码是否溢出