目录

​一、算法介绍

1.算法思想

2.算法流程

二、算法实现

1.代码实现

2.测试用例及结果

三、性能分析

1.时间复杂度

2.空间复杂度

---

​一、算法介绍

1.算法思想

折半插入排序的思想是借用了折半查找的思路，通过在已经有序的序列（默认序列第一个元素为有序序列）中利用二分查找快速定位插入位置，这样经过n-1趟插入就能完成排序，当元素较多时，折半插入排序效率更优于直接插入排序。

2.算法流程

默认序列第一个元素是已经有序序列，每次从无序序列中拿取一个元素，通过折半查找快速找到在有序序列中的插入位置，然后插入元素，经过n-1趟插入完成排序。默认排升序。

示例：

待排序序列：4，2，8，9，5，6，1，3，7

​

二、算法实现

1.代码实现

#include
using namespace std;
 
void BinarySearch(int* arr, int size) {//折半插入排序
	for (int i = 1; i < size; i++) {//默认第一个元素为有序序列，所以从1开始循环
		if (arr[i] < arr[i - 1]) {//如果当前元素大于等于有序序列所有元素，不需要进行查找插入
			int  key = arr[i];//标记待插入元素
			int left = 0;
			int right = i - 1;
			while (left <= right) {
				int mid = (left + right) / 2;
				if (arr[mid] > key) {
					right = mid - 1;
				}
				else {
					left = mid + 1;
				}
			}
			for (int j = i - 1; j > right; j--) {//顺序后移
				arr[j + 1] = arr[j];
			}
			arr[right + 1] = key;//插入元素
		}
	}
}
 
void PrintArr(int* arr, int size) {//数组打印
	cout << endl;
	for (int i = 0; i < size; i++) {
		cout << arr[i] << ' ';
	}
}
 
void Test() {
	int arr[] = { 4,2,8,9,5,6,1,3,7 };
	//int arr[] = { 15,1,1,45,12,125,15,45,20,-3 };
	int size = sizeof(arr) / sizeof(arr[0]);
 
	cout << "排序前：";
	PrintArr(arr, size);
	BinarySearch(arr, size);
	cout << endl << "排序后：";
	PrintArr(arr, size);
}
 
int main() {
	Test();
	return 0;
}

2.测试用例及结果

测试用例1：4，2，8，9，5，6，1，3，7

测试结果：

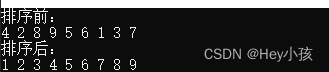
测试用例2：15，1，1，45，12，125，15，45，20，-3 

测试结果：

 

三、性能分析

1.时间复杂度

最坏情况：

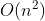根据算法思想可知，最坏情况即元素刚好与排序要求相反的情况，每次都需要进行位置折半查找，虽然利用折半查找提高了查找性能，但是移动元素的次数是固定的，所以最坏情况下的时间复杂度为。

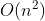最好情况：

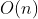最好情况自然就是元素本身已经有序的情况下，那么每个元素只需要在开始时的一次比较就确认已经处于对应位置，不再需要进行折半查找插入，因此最好情况下的时间复杂度为。

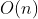平均情况  ：

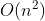综合两种情况，折半插入排序的时间复杂度为 。

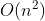2.空间复杂度

由于算法实现中只使用了几个临时变量作为标记，没有借助额外的辅助空间，所以空间复杂度为O(1)。

活动地址：CSDN21天学习挑战赛

​