---

一、基于密度的聚类DBSCAN算法

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。 该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

动画讲解DBSCAN算法的国外网站：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

1.1DBSCAN算法的基本概念

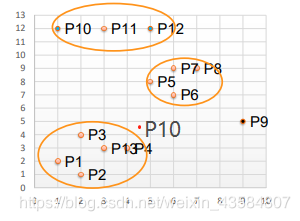
1.取半径为3，MinPts为3（圆圈能够圈住的最小的数目），则可以得到如下的分类结果，其中，P9为噪音点，P10为噪音点。

• MinPts:这个参数就是圆能够圈住的点的个数，也相当于是一个密度，一般这个值都是偏小一些，然后进行多次尝试

• （1）Eps邻域：给定对象半径Eps内的邻域称为该对象的Eps邻域。

• （2）核心点（core point）：如果对象的Eps邻域至少包含最小数目MinPts的对象，则称该对象为核心对象。

• （3）边界点（edge point）：边界点不是核心点，但落在某个核心点的邻域内。

• （4）噪音点（outlier point）：既不是核心点，也不是边界点的任何点。6，

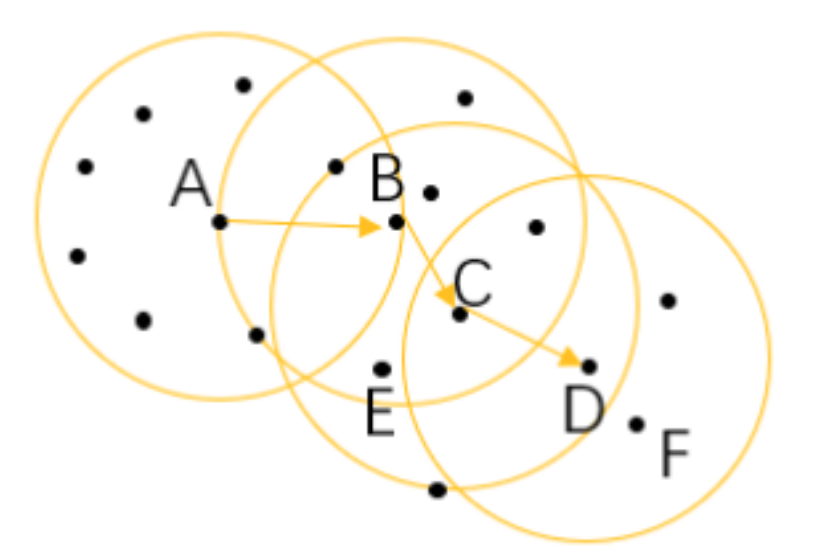
• 我们假设最小样本容量为6，A、B、C为核心对象：
  

• （5） 直接密度可达：给定一个对象集合D，如果p在q的Eps邻域内，而q是一个核心对象，则称对象p从对象q出发时是直接密度可达的，比如 上图中的 A 和 B 、B 和 C 等。

• （6）密度可达： 如果有一系列的点，都满足上一个点到这个点是密度直达，那么这个系列中不相邻的点就称为密度可达，比如 A 和 D。

• （7）密度相连： 如果存在对象O∈D，使对象p和q都是从O关于Eps和MinPts密度可达的，那么对象p到q是关于Eps和MinPts密度相连的，比如这 里的 E 和 F 点就是密度相连。

1.2DBSCAN算法参数选择

半径： 半径是最难指定的 ，大了，圈住的点就多了，簇的个数就少了；反之，圈住的点少了，簇的个数就多了，这对我们最后的结果是有影响的。我们这个时候K距离可以帮助我们来设定半径r，也就是要找到突变点，比如：

1.3DBSCAN算法原理

• （1）DBSCAN通过检查数据集中每点的Eps邻域来搜索簇，如果点p的Eps邻域包含的点多于MinPts个，则创建一个以p为核心对象的簇；
• （2）然后，DBSCAN迭代地聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并；
• （3）当没有新的点添加到任何簇时，该过程结束。

DBSCAN 算法的簇里面可以有一个或者多个核心点。如果只有一个核心点，则簇里其他的非核心点样本都在这个核心点的 Eps 邻域里。如果有多个核心点，则簇里的任意一个核心点的 Eps 邻域中一定有一个其他的核心点，否则这两个核心点无法密度可达。这些核心点的 Eps 邻域里所有的样本的集合组成一个 DBSCAN 聚类簇。

DBSCAN算法的描述如下。

输入：数据集，邻域半径 Eps，邻域中数据对象数目阈值 MinPts;
输出：密度联通簇。
处理流程如下。

• 1）从数据集中任意选取一个数据对象点 p；
• 2）如果对于参数 Eps 和 MinPts，所选取的数据对象点 p 为核心点，则找出所有从 p 密度可达的数据对象点，形成一个簇；
• 3）如果选取的数据对象点 p 是边缘点，选取另一个数据对象点；
• 4）重复（2）、（3）步，直到所有点被处理。

DBSCAN 算法的计算复杂的度为 O(n²)，n 为数据对象的数目。这种算法对于输入参数 Eps 和 MinPts 是敏感的。

1.4DBSCAN算法中dbscan()函数的说明

dbscan(X, eps=0.5, *, min_samples=5, metric='minkowski',
       metric_params=None, algorithm='auto', leaf_size=30,
       p=2, sample_weight=None, n_jobs=None)
1
2
3

参数说明：

• eps : float, optional
  两个样本之间的最大距离，一个被认为是另一个样本的邻域。这不是群集中点的距离的最大界限。这是为您的数据集和距离函数选择适当的最重要的DBSCAN参数。

• min_samples ： int，可选
  对于要被视为核心对象的点，邻域中的样本数（或总权重）。这包括点本身。

• metric：最近邻距离度量参数。默认的欧式距离（即p=2的闵可夫斯基距离），可以使用的距离度量参数有：欧式距离 “euclidean”，曼哈顿距离 “manhattan”，切比雪夫距离“chebyshev”，闵可夫斯基距离 “minkowski”，带权重闵可夫斯基距离 “wminkowski”，标准化欧式距离 “seuclidean”，马氏距离“mahalanobis”。

• metric_params : dict, optional
  度量函数的其他关键字参数。

• algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，可选
  NearestNeighbors模块用于计算逐点距离并找到最近邻居的算法。有关详细信息，请参阅NearestNeighbors模块文档。

• leaf_size ： int，optional（默认值= 30）
  叶子大小传递给BallTree或cKDTree。这可能会影响构造和查询的速度，以及存储树所需的内存。最佳值取决于问题的性质。

• p ： float，可选
  正确译法：用于计算点之间距离的Minkowski矩阵的幂。

• n_jobs ： int或None，可选（默认=无）
  要运行的并行作业数。 None除非在joblib.parallel_backend上下文中，否则表示1 。 -1表示使用所有处理器。

1.5DBSCAN算法的实现

import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.cluster import dbscan

#  make_moons 这个方法是生成两个交错的半圆环
data,_ = datasets.make_moons(500,noise = 0.1,random_state=1)   # 创建数据集
# print('数据集0，1', data)
df = pd.DataFrame(data,columns = ['feature1','feature2'])     # 将数据集转换为dataframe
# 可视化处理
# 绘制样本点，s为样本点大小，aplha为透明度，设置图形名称
# 看下面第1个图
df.plot.scatter('feature1','feature2', s = 100,alpha = 0.6, 
                title = 'dataset by make_moon')

# DBSCAN算法
core_samples,cluster_ids = dbscan(data, eps = 0.2, min_samples=20) # eps为邻域半径，min_samples为最少点数目
# cluster_id=k，k为非负整数时，表示对应的点属于第k簇，k为簇的编号，当k=-1时，表示对应的点为噪音点
# print('标签', cluster_ids)

# np.c_用于合并按行两个矩阵
#（要求两个矩阵行数相等，这里表示将样本数据特征与对应的簇编号连接）
df = pd.DataFrame(np.c_[data,cluster_ids],columns = ['feature1','feature2','cluster_id'])
# print('两个矩阵合并后的DataFrame', df)
# astype函数用于将pandas对象强制转换类型，这里将浮点数转换为整数类型
df['cluster_id'] = df['cluster_id'].astype('int')


# 绘图，c = list(df['cluster_id'])表示样本点颜色按其簇的编号绘制
# cmap=rainbow_r表示颜色从绿到黄
# colorbar = False表示删去显示色阶的颜色栏
# 看下面第2个图
df.plot.scatter('feature1','feature2', s = 100,
    c = list(df['cluster_id']),cmap = 'Reds',colorbar = False,
    alpha = 0.6,title = 'DBSCAN cluster result')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

图1：未运用DBSCAN算法进行处理的数据散点图

图2：运用DBSCAN算法进行处理的数据散点图

二、基于层次的聚类Birch算法

Birch聚类算法称为平衡迭代归约及聚类算法，它是一种常用的层次聚类算法。该算法通过聚类特征（Clustering Feature，CF）和聚类特征树（Clustering Feature Tree，CFT）两个概念描述聚类。聚类特征树用来概括聚类的有用信息，由于其占用空间小并且可以存放在内存中，从而提高了算法的聚类速度，产生了较高的聚类质量，并适用于大型数据集。层次聚类算法是讲数据样本组成一颗聚类树，根据层次分解是以自顶向下（分裂）还是自底向上（合并）方式进一步合并或分裂。

2.1Birch算法描述

Birch聚类算法具有能处理的数据规模大、算法效率高、更容易计算类簇的直径和类簇之间的距离等优点。

Birch聚类算法的聚类特征（CF）通过三元组结构描述了聚类类簇的基本信息，
三元结构公式为：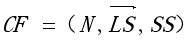

上述中N表示聚类数据点的个数，每个点用一个d维向量表示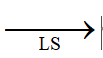；表示N个聚类数据点的线性和；SS表示N个聚类数据点的平方和。聚类特征通过线性和表示聚类的质心，通过平方和表示聚类的直径大小。

Birch算法主要包括以下三个阶段：

• 定初始阈值z并扫描整个数据集D，再根据该阈值建立一棵聚类特征树T。
• 通过提升阈值z重建该聚类特征树T，从而得到一棵压缩的CF树。
• 利用全局性聚类算法对CF树进行聚类，改进聚类质量以得到更好的聚类结果。

2.2Birch()函数使用

1. 在Sklearn机器学习包中，调用cluster聚类子库的Birch()函数即可进行Birch聚类运算，该算法要求输入聚类类簇数。Birch类构造方法如下：

Birch(branching_factor=50, compute_labels=True, 
      copy=True, n_clusters=3, threshold=0.5)
1
2

参数说明：

• branches_factor：每个节点中CF子集群的最大数量,默认为50。
• n_clusters ：聚类的目标个数（可选）。最重要的参数n_clusters=3表示该聚类类簇数为3，即聚集成3堆。
• threshold ：扫描半径（个人理解，官方说法比较绕口），设置小了分类就多。
• compute_labels布尔：默认值 =True，是否计算每个拟合的标签。
• copy：默认值 = Ture
  是否创建给定数据的副本。如果设置为 False，则初始数据将被覆盖。

2. 下面举个简单的实例，使用前面的例子中的6个点进行，设置聚类类簇数为2（n_clusters=2），调用Birch()函数聚类，通过clf.fit()装载数据训练模型。

from sklearn.cluster import Birch
X = [[1,1],[2,1],[1,3],[6,6],[8,5],[7,8]]
y = [0,0,0,1,1,1]
clf = Birch(n_clusters=2) # 聚类模型
clf.fit(X,y)             # 训练
print(clf.labels_)      # 聚类后的类标 , 从0开始的数字
1
2
3
4
5
6

输出为：

[1 1 1 0 0 0]
1

clf.labels_表示输出聚类后的类标。由于聚类类簇设置为2，故类标为0或1，其中X[1,1]、X[2,1]、X[1,3]聚类后属于1类，X[6,6]、X[8,5]、X[7,8]聚类后属于0类。

2.3Brich算法的使用

氧化物数据下载：http://archive.ics.uci.edu/ml/machine-learning-databases/glass/
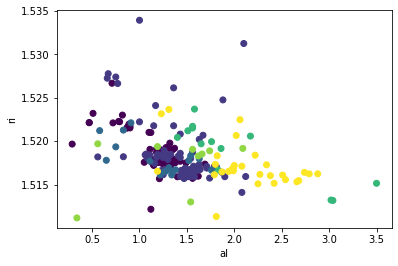
其中数据集共包含9个特征变量，分别为ri、na、mg、al、si、k、ca、ba、fe，1个类别变量glass_type，共有214个样本。其中类别变量glass_type包括7个值，分别是：1 表示浮动处理的窗口类型、2表示非浮动处理的窗口类型、3表示浮动处理的加工窗口类型、4表示非浮动处理的加工窗口类型（该类型在该数据集中不存在）、5表示集装箱类型、6表示餐具类型、7表示头灯类型。

1. 散点图的简单实现

import pandas as pd
import matplotlib.pyplot as plt

glass = pd.read_csv("glass1.csv") # 读取glass1.csv文件
# 不同类别glass_type绘制为不同颜色的点（共7个类别）
plt.scatter(glass.al, glass.ri, c=glass.glass_type)
plt.xlabel('al')
plt.ylabel('ri')
plt.show()
1
2
3
4
5
6
7
8
9

散点图为：

• Brich算法的实现
  主要步骤为：
• 调用Pandas扩展包的read_csv导入玻璃数据集，注意获取两列数据，需要转换为二维数组X。
• 从sklearn.cluster包中导入Birch()聚类函数，并设置聚类类簇数。 调用clf.fit(X, y)函数训练模型。
• 用训练得到的模型进行预测分析，调用predict()函数预测数据集。 分别获取三类数据集对应类的点。
• 调用plot()函数绘制散点图，不同类别的数据集设置为不同样式。

代码为：

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import Birch

# 数据获取
glass=pd.read_csv("glass1.csv")
X1 = glass.al                  # 获取第五列数据
X2 = glass.ri                  # 获取第二列数据
T = dict(zip(X1,X2))           # 生成二维数组   
X = list(map(lambda x,y: (x,y), T.keys(),T.values())) # dict类型转换为list 
y = glass.glass_type           # 获取第11列数据

# 聚类
clf = Birch(n_clusters=3)# n_clusters=3表示该聚类类簇数为3，即聚集成3堆
clf.fit(X, y)            # 训练
y_pred = clf.predict(X)  # 预测
print('预测结果=', y_pred)

# 分别获取不同类别数据点 
x1, y1 = [], []   
x2, y2 = [], [] 
x3, y3 = [], []

# 分布获取类标为0、1、2的数据并赋值给(x1,y1) (x2,y2) (x3,y3) 
i = 0  
while i < len(X):  
    if y_pred[i]==0:  
        x1.append(X[i][0])  
        y1.append(X[i][1])  
    elif y_pred[i]==1:  
        x2.append(X[i][0])  
        y2.append(X[i][1])  
    elif y_pred[i]==2:  
        x3.append(X[i][0])  
        y3.append(X[i][1])  
    i = i + 1  
  
# 三种颜色 红 绿 蓝，marker='x'表示类型，o表示圆点 *表示星型 x表示点   
plot1, = plt.plot(x1, y1, 'or', marker="x")    
plot2, = plt.plot(x2, y2, 'og', marker="o")    
plot3, = plt.plot(x3, y3, 'ob', marker="*")
plt.xlabel('al')
plt.ylabel('ri')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

输出为：

预测结果= [2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 0 2 2 0 2 0
 0 0 2 2 2 0 2 2 0 2 2 2 2 2 1 1 2 1 2 2 1 2 2 2 2 2 2 0 0 1 1 2 0 0 0 0 2
 2 2 2 2 2 2 2 2 2 0 2 0 2 1 2 2 2 1 1 1 2 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 2 2 1 1 1 1]
1
2
3
4

散点图：

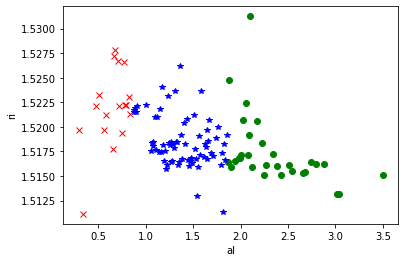
从图中可以看到，右下角红色x形点聚集在一起，其al含量较高、ri含量较低；中间绿色o点聚集在一起，其al、ri含量均匀；右部蓝色*星形点聚集在一起，其al含量较低、ri含量较高。可以看出Birch算法将数据集划分为三部分。

---

总结

DBSCAN算法优缺点

优点

• 1）不需要划分个数。 跟 K-means 比起来，DBSCAN 不需要人为地制定划分的类别个数，而可以通 过计算过程自动分出。
• 2）可以处理噪声点。 经过 DBSCAN 的计算，那些距离较远的数据不会被记入到任何一个簇中，从而成为噪声点，这个特色也可以用来寻找异常点。
• 3）可以处理任意形状的空间聚类问题。 从我们的例子就可以看出来，与 K-means不同，DBSCAN 可以处理各种奇怪的形状，只要这些数据够稠密就可以了。

缺点

• 1）需要指定最小样本量和半径两个参数。 这对于开发人员极其困难，要对数据非常了解并进行很好的数据分析。而且根据整个算法的过程可以看出，DBSCAN 对这两个参数十分敏感，如果这两个参数设定得不准确，最终的效果也会受到很大的影响。
• 2）数据量大时开销也很大。在计算过程中，需要对每个簇的关系进行管理。所以当数据量大的话， 内存的消耗也非常严重。
• 3）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差。

Birch算法优缺点

优点

• 1)节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针。
• 2)聚类速度快，只需要一遍扫描训练集就可以建立CFTree，CF Tree的增删改都很快。
• 3)可以识别噪音点，还可以对数据集进行初步分类的预处理 。
• 4)可以不用输入类别数K值。如果不输入K值，则最后的CF元组的组数即为最终的K，否则会按照输入的K值对CF元组按距离大小进行合并。

缺点

• 1)由于CFTree对每个节点的CF个数有限制，导致聚类的结果可能和真实的类别分布不同，一个CF数节点并不总是对应于用户所考虑的一个自然簇 。
• 2)对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means 。
• 3)因为其使用半径或者直径的概念来定义簇的边界，所以如果数据集的分布簇不是类似于超球体，或者说不是凸的，则聚类效果不好。
• 4)BIirch适合于处理需要数十上百小时聚类的数据，但在整个过程中算法一旦中断，一切必须从头再来。