PyTorch笔记 - Convolution卷积的原理 (2)

卷积操作示意图：

• 蓝色是input feature map = 5x5
• 深蓝色是kernel = 3x3
• 绿色是output feature map = 3x3
• stride是1，pad是0
• O = (I-K+2P)/S+1，即(5-3+0)/1+1 = 3

修改padding和stride：

• 将input feature map进行pad操作，左右+1，即padding=1，5x5 -> 7x7
• 将stride修改为2
• O = (I-K+2P)/S+1，即(5-3+2)/2+1 = 3

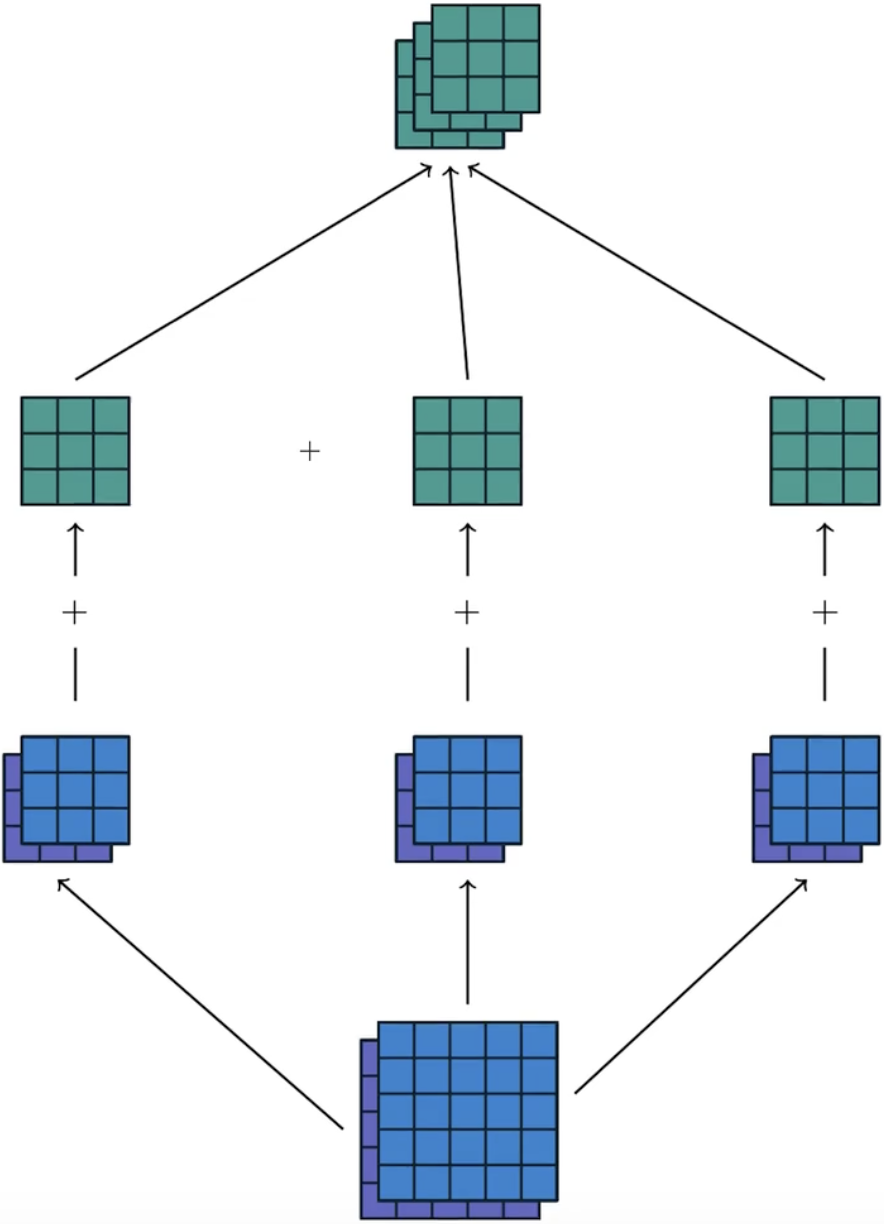
多通道卷积：

• in_channels = 2，out_channels = 3
• 从下向上，第2行是kernel，即2个3x3的kernel

Padding是{‘valid’, ‘same’}

• padding='valid' is the same as no padding.
• padding='same' pads the input so the output has the shape as the input. However, this mode doesn’t support any stride values other than 1. same不支持stride大于1

用原始的矩阵运算来实现二维卷积, 先不考虑batchsize维度和channel维度：

• 支持bias、stride、padding
• 验证 矩阵运算实现卷积的结果 = 调用PyTorch API的卷积实现结果

# step1 用原始的矩阵运算来实现二维卷积, 先不考虑batchsize维度和channel维度

input = torch.randn(5, 5)  # 卷积输入特征图
kernel = torch.randn(3, 3)  # 卷积核
bias = torch.randn(1)  # 卷积偏置，默认输出通道数是1

def matrix_multiplication_for_conv2d(input, kernel, bias=0, stride=1, padding=0):
    if padding > 0:
        input = F.pad(input, (padding, padding, padding, padding))
    input_h, input_w = input.shape
    kernel_h, kernel_w = kernel.shape
    # 向下取整floor, 直接pad到input，不用padding
    output_w = int((input_w - kernel_w) / stride + 1)  # 卷积输出的高度
    output_h = int((input_h - kernel_h) / stride + 1)  # 卷积输出的宽度
    
    output = torch.zeros(output_h, output_w)  # 初始化输出矩阵
    
    for i in range(0, input_h-kernel_h+1, stride):  # 对高度维进行遍历
        for j in range(0, input_w-kernel_w+1, stride):  # 对宽度度维进行遍历
            region = input[i:i+kernel_h, j:j+kernel_w]
            output[int(i/stride), int(j/stride)] = torch.sum(region * kernel) + bias  # 点乘，并且赋值输出位置的元素
    
    return output

# 矩阵运算实现卷积的结果
mat_mul_conv_output = matrix_multiplication_for_conv2d(input, kernel, bias=bias, padding=1)
print(f'mat_mul_conv_output: \n{mat_mul_conv_output}')

# 调用PyTorch API的卷积实现结果, padding=1, padding="same"
mat_mul_conv_output = F.conv2d(input.reshape((1,1,*input.shape)), kernel.reshape(1, 1, *kernel.shape), bias=bias, padding="same")
print(f'mat_mul_conv_output: \n{mat_mul_conv_output.reshape(mat_mul_conv_output.shape[2:])}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31