算法篇：查找算法

一、查找算法概述

1. 查找算法

• 查找：根据给定的值，在查找表中确定一个关键字等于给定值的元素
• 分类：
  • 静态查找和动态查找
    • 动态查找指查找表中有删除和插入的操作
  • 无序查找和有序查找
    • 无序查找：被查找数列有序无序均可
    • 有序查找：被查找数列必须有序

2. 常见查找算法

• 顺序查找
• 二分查找
• 插值查找
• 斐波那契查找

二、常见查找算法

1. 顺序查找

• 思路
  • 一种无序查找算法。从数据结构线性表一端开始，顺序扫描，将扫描得到的结点关键字与给定值进行比较
• 复杂度：
  • 时间复杂度：O(n)

public boolean sequenceSearch(List<Integer> list, int target){
	int size = list.size();
    for(int i = 0; i < size; i++){
    	if(target == list.get(i)){
    		return true;
    	}
    }
    return false;
}
1
2
3
4
5
6
7
8
9

2. 二分查找

• 思路
  • 一种有序查找算法。将给定值与中间结点的关键词比较，相等查找成功，不相等则根据比较结果确定查找那个子表，递归进行
• 时间复杂度
  • 时间复杂度：O(log2n)
• 特点
  • 适用于有序、静态查找，频繁插入和删除的数据集不适用

// list是升序列表
public boolean binarySearch(List<Integer> list, int target){
	int low = 0, high = list.size() - 1, mid;
	while(low <= high){
		mid = (low + high) / 2;
		if(target == list.get(mid)){
			return true;
		} else if(list.get(mid) < target){
			left = mid + 1;
		} else {
			right = mid - 1;
		}
	}
	return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

3. 插值查找

• 思路
  • 一种有序查找算法，是对二分查找算法的改进，根据关键字在有序表中所处的位置进行查找，而不是直接一般的位置
  • 二分查找：mid = low + 1/2(high - low)
  • 插值查找：mid = low + (key - a[low])/(a[high] - a[low])*(high - low)
• 时间复杂度
  • O(log2n)
• 特点
  • 对于表长较大，关键字分布均匀的查找表，插值查找的平均性能比二分查找好得多；反之则未必

// list是升序列表
public boolean interplotSearch(List<Integer> list, int target){
	if(list.isEmpty()){
		return false;
	}
	int low = 0, high = list.size() - 1, mid;
	while(low <= high){
		mid = low + (target - list.get(low)) / (list.get(high)- list.get(low)) * (high - low);
		if(target == list.get(mid)){
			return true;
		} else if(list.get(mid) < target){
			low = mid + 1;
		} else {
			high = mid - 1;
		}
	}
	return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

4. 斐波那契查找

• 思路：
  • 一种有序查找算法，也是对二分查找的改进，按照黄金分割比例进行查找
  • 声明斐波那契数列为F(n)
    • 数列为：1,1,2,3,5,8,13,21,34…，随着数列递增，前后两个数的比值越接近0.618
    • 数列满足：F(n) = F(n-1) + F(n-2)
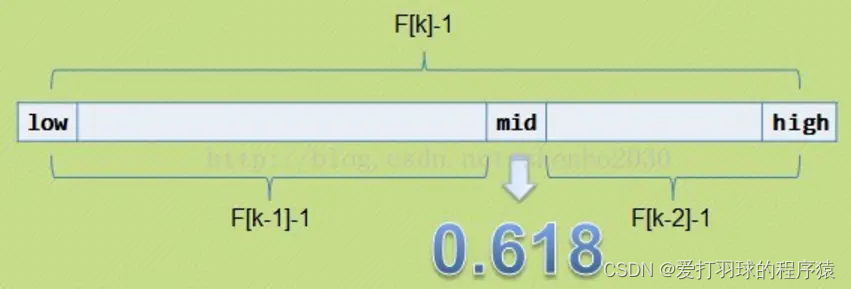
  • 要求查找序列的元素个数为某个斐波那契数 - 1，即n = F(k) - 1
  • 将给定值与F(k-1)位置的记录进行比较，mid = low + F(k-1) - 1
    • 相等即查找成功
    • 给定值大于mid位置的值，low = mid + 1，k = k - 2
    • 给定值小于mid位置的值，high = mid - 1, k = k - 1
      
• 时间复杂度
  • O(log2n)

// list是升序列表
public boolean fibonaccSearch(List<Integer> list, int target){
    if(list.isEmpty()){
        return false;
    }
    // 根据list的长度确定斐波那契数组
    int oldLen = list.size();
    List<Integer> fibs = getFibonacc(oldLen);
    // 根据fibs的最大值填充list
    int newLen = fibs.get(fibs.size() - 1) - 1;
    List<Integer> newList = new ArrayList<>(newLen);
    newList.addAll(list);
    for(int i = oldLen; i < newLen; i++){
        // 补充的元素值为list的最后一个元素的值
        newList.add(list.get(oldLen - 1));
    }
    // 开始查找
    int index = fibs.size() - 1, low = 0, high = newLen - 1, mid;
    while(low <= high){
        mid = low + fibs.get(index - 1) - 1;
        // 防止越界
        if(mid >= newLen){
            mid = newLen - 1;
        }
        if(target == newList.get(mid)){
            return true;
        } else if(newList.get(mid) < target){
            low = mid + 1;
            index -= 2;
        } else {
            high = mid - 1;
            index--;
        }
    }
    return false;
}

public List<Integer> getFibonacc(int len){
    List<Integer> fibs = new ArrayList<>();
    int tmp = 1, index = 0;
    while(len > tmp - 1){
        if(index == 0){
            tmp = 1;
        } else if(index == 1){
            tmp = 1;
        } else {
            tmp = fibs.get(index - 1) + fibs.get(index - 2);
        }
        fibs.add(tmp);
        index++;
    }
    return fibs;
}

public static void main(String[] args) {
    Search search = new Search();
    List<Integer> fibonacc = search.getFibonacc(0);
    search.fibonaccSearch(Arrays.asList(1), 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59