概念

问题1：保险柜中存放有10个人的共有财产，要从保险柜中取出物品，必须有半数以上的人在场才可取出，半数以下则不行。如何构造锁的设计方案?

问题2：导弹的发射控制、重要安保场所的通行检验，通常需要多人同时参与才能生效。因此，需要将秘密分给多人掌管，并且由一定掌管秘密的人数同时到场才能恢复秘密。方案如何设计?

这里我们就需要提出秘密共享的概念。

  秘密共享的思想是将秘密进行分割，并把秘密在$n$个参与者中分享，使得只有多于特定$t$个参与者合作才可以计算出或恢复出秘密，而少于$t$个参与者则不可以得到有关秘密。

  秘密共享的关键是怎样更好的设计 秘密拆分方式 和 恢复方式。

  秘密共享是一种将秘密分割存储的密码技术，目的是阻止秘密过于集中，以达到分散风险和容忍入侵的目的，是信息安全和数据保密中的重要手段。

注意：

1. 在对秘密进行拆分，拆分的方式不一定均匀。
2. $t$一定是小于等于$n$的。
   
   

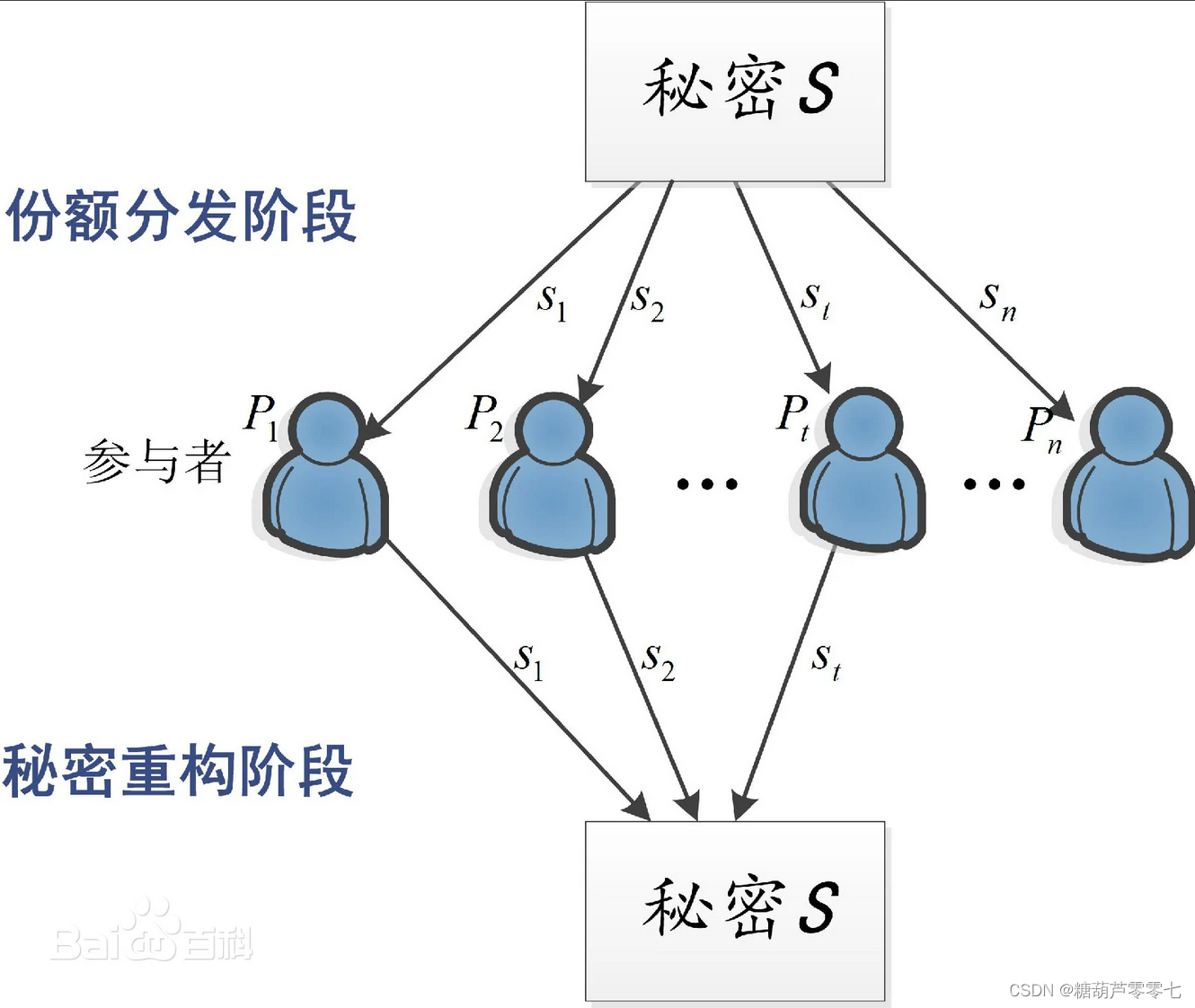
Shamir秘密共享方案

  一般的，设$\{(x_1,y_1),(x_2,y_2),......,(x_k,y_k)\}$是平面上$k$个不同的点构成的点集， 那么在平面上存在唯一的$k-1$次多项式$f(x)=a_0+a_{1}x+a_2{x}^2+.....+a_{k-1}{x}^{k-1}$通过这$k$个点。

  若把秘密$s$取做$f(0)$, $n$个份额取做$f(i)(i=1,2,....,n)$, 那么利用其中任意k个份额可以重构$f(x)$, 从而可以得到秘密$s$。

加密

  对于待加密的明文$s\in Z_p$($p$为大素数且$p>=n+1$)，在有限群$GF(p)$任取$k-1个$随机数$a_1,a_2,\dots ,a_{k-1}$并令$a_0=s$，从而构造如下的多项式：$$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+.....+a_{k-1}{x}^{k-1}mod(p)$$  对于这个多项式， 任取$n$个数$x_1,x_2,x_3,...,x_n$分别带入多项式得到$n$个密钥对$(x_i,y_i)$：$$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+.....+a_{k-1}{x}^{k-1}mod(p)$$  分发给$n$个持有者$P_1,P_2,...,P_n$。

解密

  假设得到了$k$个密钥对 { x 1 , y 1 } , { x 2 , y 2 } , . . … , { x k , y k } \{x_1, y_1\}, \{x_2, y_2\}, ..…,\{x_k,y_k\} {x1​,y1​},{x2​,y2​},..…,{xk​,yk​}，我们可以得到如下方程(运算均在$GF(p)$：$$a_0+a_1{x}_1+a_2{x}_1^2+.......+a_{k-1}{x}_1^{k-1}=y_1$$$$a_0+a_1{x}_2+a_2{x}_2^2+.......+a_{k-1}{x}_2^{k-1}=y_2$$$$a_0+a_1{x}_3+a_2{x}_3^2+.......+a_{k-1}{x}_3^{k-1}=y_3$$$$.............................................$$$$a_0+a_1{x}_k+a_2{x}_k^2+.......+a_{k-1}{x}_k^{k-1}=y_k$$  由Lagrange插值公式：$$f(x)=\sum _{i=1}^{k}f(x_i)\prod _{j=1,j\ne i}^k\frac{x-x_j}{x_i-x_j}(modp)$$  故$$f(0)=a_0=s=(-1{)}^{k-1}\sum _{i=1}^{k}f(x_i)\prod _{j=1,j\ne i}^k\frac{x_j}{x_i-x_j}(modp$$  可求的$a_0$即为明文$s$。

示例：$(3,5)$门限方案

  设 k = 3 , n = 5 , p = 19 , s = 11 , G F ( 19 ) = { 0 , 1 , 2 , 3 , 4 , . . . . , 18 } k = 3, n = 5, p = 19, s = 11, GF(19) = \{0, 1, 2, 3, 4, ...., 18\} k=3,n=5,p=19,s=11,GF(19)={0,1,2,3,4,....,18}, 随机选择系数 $a_1=2,a_2=7$.

则 $f(x)=11+2x+7x^{2}mod19$.

计算可知：$$f(1)=1$$$$f(2)=5$$$$f(3)=4$$$$f(4)=17$$$$f(5)=6$$

若已知 $f(2),f(3),f(5)$, 有拉格朗日插值公式可知：
$$f(x)=5\frac{(x-3)(x-5)}{(2-3)(2-5)}+4\frac{(x-2)(x-5)}{(3-2)(3-5)}+6\frac{(x-2)(x-3)}{(5-2)(5-3)}$$$$=11+2x+7x^2$$$$故，s=f(0)=11.$$

补充

当$k=n$的时候，Shamir算法就变成了$(n,n)$门限秘密共享。此种方式可以通过 异或运算 进行实现， 具体实现步骤如下：

1. 首先将秘密信息转成$01$字符串$s$。
2. 然后随机选取$n-1$个与$s$长度相同的01字符串$s_1,s_2,....,s_{n-1}$, 将$s$与$s_1,s_2,....,s_{n-1}$进行 异或操作，得到$s_n$。$$s_n=s\oplus s_1\oplus s_2\oplus .........\oplus s_{n-1}$$然后将$n$个秘密信息$s_1,s_2,....,s_{n-1},s_n$分配给$n$个人， 只有这n个人的时候才能解得秘密信息： $$s=s_1\oplus s_2\oplus .......\oplus s_{n-1}\oplus s_n$$

网页参考链接

1. 多方安全计算-秘密共享
2. 趣说密码学（五）秘密共享方案——shamir,中国剩余定理,Brickell和Blakley
3. MPC–秘密分享（Secret-Sharing）算法及使用Demo
4. Shamir秘密共享
5. Shamir密钥分享算法解析
6. 秘密共享算法