AcWing基础部分Class2：高精度加减乘除、前缀和与差分

1.3 高精度

C++考虑高精度，Java有大整数类，Python默认数的范围是无穷大

高精度考察的类型：

大整数相加 A和B的位数大概是10^6
大整数相减 A和B的位数大概是10^6
大整数乘以一个小整数 $len(A)\leq 10^6,a\leq10^9$
一个大整数除以一个小整数
【不常用】：大整数相除，大整数相乘

1.3.1 大整数的存储和计算

1.3.1.1 存储

将大整数的每个位存在数组里面去

存储：个位放在数组的第一个元素，原因是考虑到高位的进位，数据结构是数组时方便在末尾加上进位数。

1.3.1.2 列竖式计算

加法的列竖式

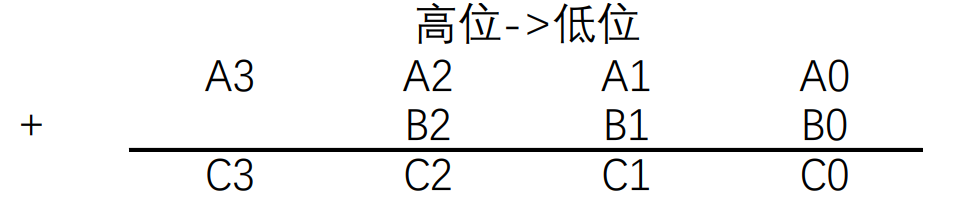
计算公式： $A_i+B_i+t=C_i$ ，其中 $t$ 代表进位，值为0或者1。

减法的列竖式

A_{i} - B_{i} - t = {\begin{cases} A_{i} - B_{i} - t, A_{i} - B_{i} - t \geq 0 \\ A_{i} - B_{i} + 10 - t, A_{i} - B_{i} - t \leq 0 \end{cases}

乘法的列竖式

     A2 A1 A0
   *        b
  ——————————————
     C2 C1 C0
1
2
3
4

{\begin{cases} t_{0} = 0 \\ C_{0} = (3 \times b + t_{0}) % 10, t_{1} = (3 \times b + t_{0}) / 10 \\ . . . \\ C_{i} = (A_{i} \times b + t_{i}) % 10, t_{i} = (A_{i} \times b + t_{i}) / 10 \end{cases}

⎩ ⎨ ⎧ t_{0} = 0 C_{0} = (3 \times b + t_{0}) %10, t_{1} = (3 \times b + t_{0}) /10 ... C_{i} = (A_{i} \times b + t_{i}) %10, t_{i} = (A_{i} \times b + t_{i}) /10

除法

1.3.2 高精度模板

1.3.2.1 高精度加法模板

class Solution {
public:
    string addStrings(string num1, string num2) {
        vector<int> Num1, Num2, Num3;
        // 字符串放入数组中：
        for (int i = num1.size() - 1; i >= 0 ; --i) {
            Num1.push_back(num1[i] - '0');  // 转换为数字放入数组中
        }
        for (int i = num2.size() - 1; i >= 0 ; --i) {
            Num2.push_back(num2[i] - '0');  // 转换为数字放入数组中
        }
        // 从数组第一位往后加
        int t = 0;
        for (int i = 0; i < Num1.size() || i < Num2.size(); ++i) {
            if (i < Num1.size()) t += Num1[i];
            if (i < Num2.size()) t += Num2[i];
            Num3.push_back(t % 10);
            t /= 10;
        }
        if (t) Num3.push_back(1);
        string num3;
        for (int i = Num3.size() - 1; i >= 0; --i) {
            num3 += Num3[i] + '0';
        }
        return num3;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

1.3.2.2 高精度减法模板

步骤：

判断：若 $A\geq B$ ，那么正常计算，否则交换A和B，计算B-A
$A_i-B_i-t=$
${\begin{cases} A_{i} - B_{i} - t, A_{i} - B_{i} - t \geq 0 \\ A_{i} - B_{i} + 10 - t, A_{i} - B_{i} - t \leq 0 \end{cases}$ $A_{i} - B_{i} - t = {A_{i} - B_{i} - t, A_{i} - B_{i} - t \geq 0 A_{i} - B_{i} + 10 - t, A_{i} - B_{i} - t \leq 0$
根据是否 $A\geq B$ 输出时考虑负号

// 高精度减法
// 判断是否有 A>=B
bool cmp(vector<int>& A, vector<int>& B) {
    if (A.size() != B.size()) return A.size() > B.size();
    // 否则长度不相等，从最高位开始判断
    for (int i = A.size() - 1; i >= 0; --i) {
        if (A[i] != B[i]) return A[i] > B[i];
    }
    return true;
}

vector<int> gaoJingDuMinus(vector<int>& A, vector<int>& B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); ++i) {    // 保证了A一定是大于B的
        int temp = A[i] - t;
        if (i < B.size()) temp -= B[i];
        C.push_back((temp + 10) % 10);  // 大于0和小于0的情况合起来写
        if (temp < 0) t = 1;
        else t = 0;
    }
    while(C.size() > 1 && C.back() == 0) C.pop_back();  // 避免出现003的情况
    return C;
}

string sub(string& a, string& b) {
    // 将字符串形式的数据存储在数组中
    vector<int> A, B, C;
    // 存储时数组的最低位存储数据的个位，以方便最高位的进位
    for (int i = a.size() - 1; i >= 0; --i) {
        A.push_back(a[i] - '0');    // 减去偏移量得到数值
    }
    for (int i = b.size() - 1; i >= 0 ; --i) {
        B.push_back(b[i] - '0');    // 减去偏移量得到数值
    }
    // 首先要判断A B哪个大，返回的数组C是逆序的，即数组的第一位是个位
    string c;
    if (cmp(A, B)) C = gaoJingDuMinus(A, B);
    else {
        C = gaoJingDuMinus(B, A);
        c.push_back('-');   // 结果应该是负数，添加一个符号
    }

    for (int i = C.size()-1; i >= 0; --i) {
        c += C[i] + '0';
    }
    return c;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

1.3.2.3 高精度乘法模板

vector<int> mul(vector<int> &A, int b) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); ++i) {
        t += (A[i] * b);
        C.push_back(t % 10);
        t = t / 10;
    }
    if (t) C.push_back(t % 10);
    return C;
}
1
2
3
4
5
6
7
8
9
10
11

1.3.2.4 高精度除法模板

// 高精度除法 A/b，商是C，余数是r    A若正存储的话比较方便，此处为了一致，仍然采取最低为
vector<int> div(vector<int>& A, int b, int& r) {
    vector<int> C;
    for (int i = A.size() - 1; i >= 0; ++i) {
        C.push_back((r * 10 + A[i]) / b);
        r = (r * 10 + A[i]) % b;
    }
    // 和A保持低位高位一样，所以reverse一下，其实不reverse的结果就是我们要输出的数据
    reverse(C.begin(), C.end());
    // 去除前导0
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

1.4 前缀和与差分

1.4.1 前缀和的概念与应用

1.4.1.1 一维前缀和

前缀和 $S [i]$ ：数组中的前i个数的和 $a_1+a_2+...+a_3$

两个问题：

如何求 $S [i]$ ？：for循环一遍即可 $S [i] = S [i - 1] + a [i]$
前缀和有什么作用：快速求出来原数组中一段数的和 $[l, r]$ 的数和—— $S [r] - S [l - 1]$

即用一次计算计算出任意一段的和

1.4.1.2 二维前缀和

主要是公式的推导，尝试题目：

剑指 Offer II 013. 二维子矩阵的和题解 - 力扣（LeetCode）

304. 二维区域和检索 - 矩阵不可变 - 力扣（LeetCode）

注意多减的要加回来。

1.4.2 模板

#include
#include

using namespace std;

int main() {
    int n, m;
    vector<int> vec, S;
    vec.push_back(0);
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        int temp = 0;
        scanf("%d", &temp);
        vec.push_back(temp);
    }
    S.push_back(0);
    for (int i = 1; i < vec.size(); ++i) {
        int temp = S[i-1] + vec[i];     // 前i-1个数的和加上i
        S.push_back(temp);
    }
    while(m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", S[r]-S[l-1]);
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

1.4.3 差分

差分是前缀和的逆过程。设有数组A，要求构造出一个数组B，使得数组A的元素 $A [i]$ 是 $B [1] ， B [2], ..., B [i]$ 的前缀和。

b称为A的差分，A是b的前缀和

所以对A求一遍差分可以得到数组b，对B求一遍前缀和得到数组A

时间复杂度都是 $O (n)$

1.4.3.1 差分数组的构造

输入数组A[i]:A[1],A[2],...,A[i]，构造其差分数组的步骤：

初始化b[i]为全0
插入A[i]等价于操作：
- b[i] = b[i] + A[i];
- b[i+1] = b[i+1] - A[i]
每输入一个A[i]，进行一次B数组的对应操作
输入完成，A的差分数组构造完成

1.4.3.2 差分的应用

构造原始的数组b[i]
对于在区间[l, c]中每个数加上c等价于操作：
- b[l] += c
- b[c+1] -= c
对数组B求一次前缀和得到最终的序列

1.4.4 模板

#include
#include

using namespace std;

// 注意书写前缀和和差分的代码时，数组下标从1开始存
int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    vector<int> nums(n+1), res(n+2,0);
    // 在输入的同时构造差分数组
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &nums[i]);
        res[i] += nums[i];
        res[i+1] -= nums[i];
    }
    // m个变化操作
    while (m--) {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        res[l] += c;
        res[r+1] -= c;
    }
    // 计算res数组的前缀和，得到最终的数组答案
    for (int i = 1; i < res.size()-1; ++i) {
        res[i] += res[i-1];
        cout << res[i] << " ";
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

习题练习 Day2

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9vNcE4yo-1660036541264)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220809162615854.png)]

对应力扣题目：

相关阅读:
局域网靶机渗透操作指南
java基于springboot+vue+nodejs大学生租房网站系统-maven
docker安装mysql
【计算思维】蓝桥杯STEMA 科技素养考试真题及解析 3
Android xml布局设置默认隐藏&&通讯
大部分人都不知道产品说明书有这些特点
云计算项目七:jump-server安装部署
安装Hive集群
【Spring云原生】Spring官宣，干掉原生JVM，推出 Spring Native！整体提升性能！Native镜像技术在Spring中的应用
HBase概述

原文地址：https://blog.csdn.net/weixin_45745854/article/details/126251882