机器学习算法——聚类1（性能度量——外部指标Jaccard系统，FM指数，Rand指数；内部指标：DB指数，Dunn指数） - 码农知识堂

机器学习算法——聚类1（性能度量——外部指标Jaccard系统，FM指数，Rand指数；内部指标：DB指数，Dunn指数）
1.聚类简介

在“无监督学习”中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。此类学习任务中研究最多、应用最广的是“聚类”。

聚类将数据集中的样本划分为若干个通常不相交的子集，每个子集称为一个“簇”（类别）。聚类过程仅能自动形成簇结构，簇所对应的概念语义需由使用者来把握和命名。

形式化表达如下：

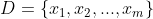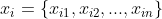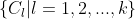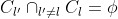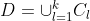
假定样本集 $D=\{x_1,x_2,...,x_m\}$ 包含m个无标记的样本，每个样本 $x_i=\{x_{i1},x_{i2},...,x_{in}\}$ 是一个n维特征向量，则聚类算法将样本集D划分为k个不相交的簇 $\{C_{l}|l=1,2,...,k\}$ ,其中 $C_{l'} \cap_{l'\neq l} C_{l} = \phi$ 且 $D=\cup^{k}_{l=1} C_l$

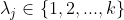相应地，用 $\lambda_j \in \{1,2,...,k\}$ 表示样本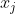的“簇标记”，即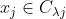 $x_j \in C_{\lambda j}$

则，聚类的结果可用包含m个元素的簇标记向量 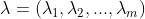$\lambda = (\lambda_1,\lambda_2,...,\lambda_m)$ 表示。

聚类既能作为一个单独过程，用于寻找数据内在的分布结构，也可作为分类等其他学习任务的前驱过程。

2. 聚类的性能度量

聚类性能度量亦称聚类“有效性指标”。对聚类结果，我们需通过某种性能度量来评估其好坏；另一方面，若明确了最终将要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而更好地得到符合要求的聚类结果。

什么样的聚类结果比较好呢？我们希望物以类聚，即同一簇的样本尽可能彼此相似，不同簇的样本尽可能不同。换言之，聚类结果的“簇内相似度高”且“簇间相似度低”。

聚类性能指标大致有两类：一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”。

另一类是直接考察聚类结果而不利用任何参考模型，称为“内部指标”。

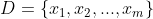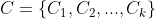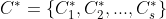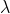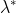对数据集 $D=\{x_1,x_2,...,x_m\}$ ，假定通过聚类给出的簇划分为 $C=\{C_1,C_2,...,C_k\}$ ，参考模型给出的簇划分为 $C^*=\{C^*_1, C^*_2,...,C^*_s\}$ 。相应地，令 $\lambda$ 与 $\lambda^*$ 分别表示与C和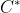对应的簇标记向量。我们将样本两两配对考虑，定义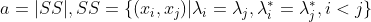

$a=|SS|, SS=\{(x_i,x_j)|\lambda_i = \lambda_j, \lambda^*_i = \lambda^*_j, i<j\}$

$b=|SD|, SD=\{(x_i,x_j)|\lambda_i=\lambda_j,\lambda^*_i \neq \lambda^*_j,i<j \}$

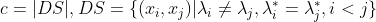
$c = |DS|, DS=\{(x_i,x_j)|\lambda_i\neq \lambda_j, \lambda^*_i = \lambda^*_j, i<j\}$

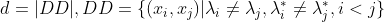
$d = |DD|, DD=\{(x_i,x_j)|\lambda_i \neq \lambda_j, \lambda^*_i \neq \lambda^*_j, i<j\}$

其中

集合SS包含了C中隶属于相同簇且在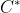中也隶属于相同簇的样本对

集合SD包含了C中隶属于相同簇但在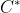中隶属于不同簇的样本对

由于每个样本对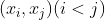仅能出现在一个集合中，因此有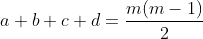

$a+b+c+d = \frac{m(m-1)}{2}$

基于上述式子，可导出下面这些常用的聚类性能度量外部指标：
- Jaccard系数（简称JC，用于比较有限样本集之间的相似性与差异性，JC系数越大，样本相似度越高）：
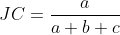
$JC = \frac{a}{a+b+c}$
- FM指数（简称FMI）
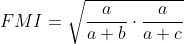
$FMI=\sqrt{\frac{a}{a+b}\cdot\frac{a}{a+c}}$
- Rand指数（简称RI）
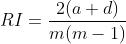
$RI=\frac{2(a+d)}{m(m-1)}$

显然，上述性能度量的结果值均在[0,1]区间，值越大越好。

考虑聚类结果的簇划分 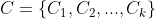$C=\{C_1,C_2,...,C_k\}$ ，定义

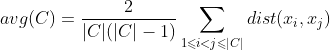
$avg(C) = \frac{2}{|C|(|C|-1)} \sum_{1\leqslant i < j \leqslant|C|}dist(x_i,x_j)$

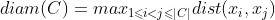
$diam(C) = max_{1 \leqslant i < j \leqslant |C|} dist(x_i,x_j)$

$d_{min}(C_i,C_j) = min_{x_i \in C_i, x_j \in C_j} dist(x_i,x_j)$

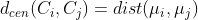
$d_{cen}(C_i,C_j) = dist(\mu_i, \mu_j)$

其中，dist(.,.)用于计算两个样本之间的距离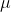； $\mu$ 代表簇C的中心点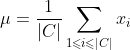 $\mu=\frac{1}{|C|}\sum_{1\leqslant i \leqslant |C|} x_i$

avg(C)对应于簇C内样本间的平均距离

diam(C)对应于簇C内样本间的最远距离

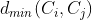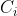$d_{min}(C_i,C_j)$ 对应于簇与簇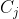最近样本间距离

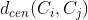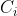$d_{cen}(C_i,C_j)$ 对应于簇与簇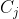中心点间的距离

基于上式可导出常用的聚类性能度量内部指标：
- DB指数（简称DBI）
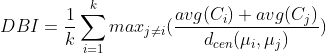
$DBI= \frac{1}{k} \sum_{i=1}^{k} max_{j \neq i} (\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)})$
- Dunn指数（简称DI）
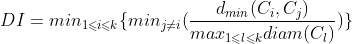
$DI= min_{1\leqslant i \leqslant k}\{min_{j \neq i} (\frac{d_{min}(C_i,C_j)}{max_{1\leqslant l \leqslant k}diam(C_l)})\}$

显然DBI的值越小越好， DI的值越大越好。‘；
相关阅读:
新手学PCB画板选什么软件
 超详细的 pytest 教程（一）使用入门篇
 十一假期，分享几个好玩儿的GitHub项目
 MPI 快速入门
 VUE element-ui之form表单中input输入超过规定长度error提醒，并实时显示输入长度，可无限输入
 GeneratePress：全局颜色设置教程
 前后端必知必会的HTTP，这份全彩版图解手册可算是给讲透了
 spring security 认证简介
 Python迭代器和生成器
 C++ -- 学习系列 std::array 容器
原文地址：https://blog.csdn.net/Vicky_xiduoduo/article/details/126235309