互质与欧拉函数

定义

        ，若，则称 a，b 互质

        对于三个数或更多数的情况，我们把 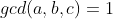 的情况称为 a, b, c 互质。

把 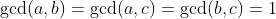 称为 a，b，c 两两互质。后者显然是一个更强的条件

欧拉函数

        1 ~ N 中与 N 互质的数的个数被称为欧拉函数，记为  

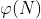
        若在算数基本定理中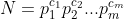，，则：

 证明：

        设 p 是 N 的质因子，1 ~ N 中 p 的倍数有 p, 2p, 3p, ..., (N/P) * p, 共 N/p 个。 

同理，若 q 也是 N 的质因子，则 1 ~ N 中 q 的倍数有 N/q 个。如果我们把这 N/p + N/q 个数去掉，那么 p * q 的倍数就被排除了两次，需要再加回来一次。因此，1 ~ N 中不与 N 含有共同质因子的 p 或 q 的个数为：

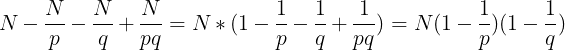
         实际上，上述思想被称为容斥原理。类似的，我们可以在 N 的全部质因子上使用容斥原理，就能得到 1 ~ N  中不与 N 含有共同质因子的数的个数，也是就是与 N 互质的个数

证毕。

AcWing 873. 欧拉函数  

输入样例：

3
3
6
8

输出样例：

2
2
4

#include 
#include 
using namespace std;
 
int main()
{
    int n;
    cin >> n;
    
    while(n -- )
    {
        int a; cin >> a;
        
        int res = a;
        for(int i = 2; i <= a / i; i ++ )
            if(a % i == 0)
            {
                res = res / i * (i - 1);
                while(a % i == 0) a /= i;
            }
        
        if(a > 1) res = res / a * (a - 1);
        
        cout << res << endl;
    }
    return 0;
}

AcWing 874. 筛法求欧拉函数 

输入样例：

6

输出样例：

12

线性筛的算法回顾

for(int i = 2; i <= n; i ++ )
    {
        if(!st[i])
        {
            primes[cnt ++ ] = i; 
        }
        for(int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }

https://www.acwing.com/solution/content/28507/

​

#include 
#include 
#include 
 
using namespace std;
 
const int N = 1000010;
 
typedef long long LL;
 
int primes[N], cnt;
int phi[N];
bool st[N];
 
LL get_eulers(int n)
{
    phi[1] = 1;
    for(int i = 2; i <= n; i ++ )
    {
        if(!st[i])
        {
            primes[cnt ++ ] = i; 
            phi[i] = i - 1;
        }
        for(int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) 
            {
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }
    
    LL res = 0;
    for(int i = 1; i <= n; i ++ ) res += phi[i];
    return res;
}
 
int main()
{
    int n;
    cin >> n;
    
    cout << get_eulers(n) << endl;
    
    return 0;
}

欧拉定理

若 a 与 n 互质，则 

 AcWing 875. 快速幂

 ​

输入样例：

2
3 2 5
4 3 9

输出样例：

4
1

​

#include 
#include 
 
using namespace std;
 
typedef long long LL;
 
int n;
 
int qmi(int a, int k, int p)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}
 
int main()
{
    cin >> n;
    while(n -- )
    {
        int a, k, p;
        scanf("%d%d%d", &a, &k, &p);
        
        printf("%d\n", qmi(a, k, p));
    }
    
    return 0;
}

AcWing 876. 快速幂求逆元

 

输入样例：

3
4 3
8 5
6 3

输出样例：

1
2
impossible

#include 
#include 
 
using namespace std;
 
typedef long long LL;
 
LL qmi(int a, int b, int p)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % p;
        a = a * (LL)a % p;
        b >>= 1;
    }
    return res;
}
 
int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        int a, p;
        cin >> a >> p;
        
        int res = qmi(a, p - 2,p);
        if(a % p) cout << res << endl;
        else puts("impossible");
    }
    return 0;
}

扩展欧几里得算法

裴蜀定理

        对于任意的整数 a，b，一定存在一对整数非0 x，y，满足  

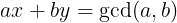
AcWing 877. 扩展欧几里得算法        

输入样例：

2
4 6
8 18

输出样例：

-1 1
-2 1

扩展欧几里得 

对于求解更一般的方程 ax+by=c 

应用: 求解一次同余方程 ax≡b(modm) 

AcWing 877. 扩展欧几里得算法 - AcWing 

#include 
 
using namespace std;
 
int exgcd(int a, int b, int& x, int& y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    
    int d = exgcd(b, a % b, y, x);
    
    y -= a / b * x;
    
    return d;
}
 
int main()
{
    int n; cin >> n;
    
    while(n -- )
    {
        int a, b, x, y;
        scanf("%d%d", &a, &b);
        
        exgcd(a, b, x, y);
        
        printf("%d %d\n", x, y);
    }
    return 0;
}

AcWing 878. 线性同余方程 

输入样例：

2
2 3 6
4 3 5

输出样例：

impossible
-3

#include 
 
using namespace std;
 
typedef long long LL;
 
int exgcd(int a,int b,int &x,int &y)
{
    if(!b)
    {
        x = 1,y = 0;
        return a;
    }
    int d = exgcd(b,a % b,y,x);
    y -= a / b * x;
    return d;
}
 
int main()
{
    int n;
    cin >> n;
    
    while(n --)
    {
        int a,b,m;
        scanf("%d%d%d",&a,&b,&m);
        int x,y;
        int d = exgcd(a,m,x,y);
        if(b % d) puts("impossible");
        else printf("%d\n",(LL)x * (b / d) % m);
    }
    
    return 0;
}