-
主成分分析;主成分回归分析——Hald水泥问题;主成分分析案例——各地区普通高等教育发展水平综合评价;matlab
目的
- 对原变量加以“改造”,在不致损失原变量太多信息的条件下尽可能地降低变量地维数,即用较少的“新变量”代替原来地各变量。
- 通过变换:用低维(主成分)近似高维(较全面)信息。
思想
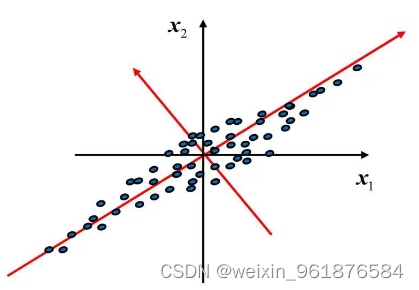
- 若有二维数据分布如上图所示,↗方向的数据分布最离散,方差最大,包含的信息最多,作为第一主成分;↖方向与第一主成分的方向是正交(信息不重叠)的,且在所有与第一主成分正交的方向中,它是最离散,方差最大的,作为第二主成分。
- 注意:上述表达只是为了方便理解主成分分析的思想,用语不是很严谨。
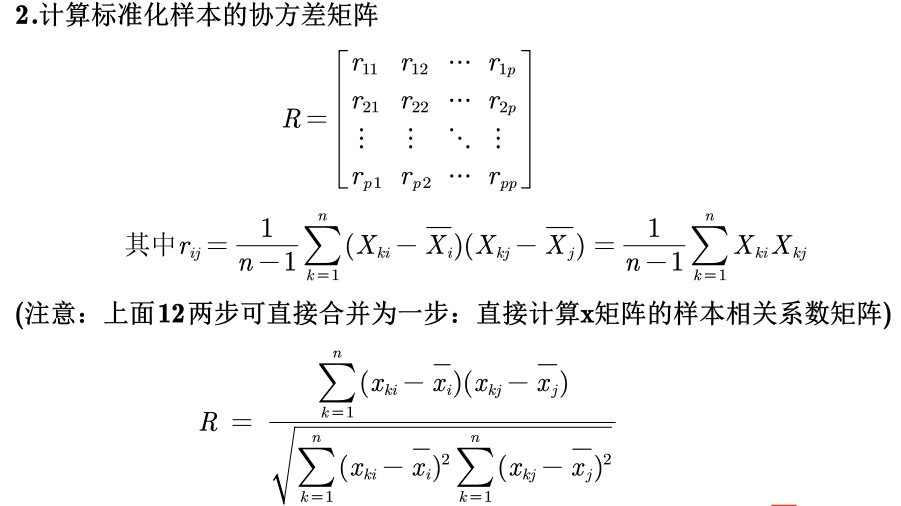
- 设 X = ( X 1 , X 2 , . . . , X p ) T X=(X_1,X_2,...,X_p)^T X=(X1,X2,...,Xp)T,协方差为
C o v ( X ) = Σ = ( σ i j ) p × p = E [ ( X − E ( X ) ) ( X − E ( X ) ) T ] Cov(X)=\Sigma=(\sigma_{ij})_{p\times p}=E[(X-E(X))(X-E(X))^T] Cov(X)=Σ=(σij)p×p=E[(X−E(X))(X−E(X))T]
- 作
Y 1 = a 1 T X = a 11 X 1 + a 12 X 2 + . . . + a 1 p X p Y_1=a_1^TX=a_{11}X_1+a_{12}X_2+...+a_{1p}X_p Y1=a1TX=a11X1+a12X2+...+a1pXp
s . t . { max V a r ( Y 1 ) = V a r ( a 1 T X ) = a 1 T Σ a 1 ( 方差最大,信息最多 ) a 1 T a 1 = 1 ( 长度不变 ) s.t.\quads.t.{maxVar(Y1)=Var(a1TX)=a1TΣa1(方差最大,信息最多)a1Ta1=1(长度不变){ max V a r ( Y 1 ) = V a r ( a 1 T X ) = a 1 T Σ a 1 ( 方 差 最 大 , 信 息 最 多 ) a 1 T a 1 = 1 ( 长 度 不 变 )
由此得第一主成分。- 作
Y 2 = a 2 T X = a 21 X 1 + a 22 X 2 + . . . + a 2 p X p Y_2=a_2^TX=a_{21}X_1+a_{22}X_2+...+a_{2p}X_p Y2=a2TX=a21X1+a22X2+...+a2pXp
s . t . { max V a r ( Y 1 ) = V a r ( a 1 T X ) = a 1 T Σ a 1 a 1 T a 1 = 1 C o v ( Y 2 , Y 1 ) = C o v ( a 2 T X , a 1 T X ) = a 2 T Σ a 1 = 0 ( 和前面的向量不相关 ) s.t.\quads.t.⎩ ⎨ ⎧maxVar(Y1)=Var(a1TX)=a1TΣa1a1Ta1=1Cov(Y2,Y1)=Cov(a2TX,a1TX)=a2TΣa1=0(和前面的向量不相关){ max V a r ( Y 1 ) = V a r ( a 1 T X ) = a 1 T Σ a 1 a 1 T a 1 = 1 C o v ( Y 2 , Y 1 ) = C o v ( a 2 T X , a 1 T X ) = a 2 T Σ a 1 = 0 ( 和 前 面 的 向 量 不 相 关 )
由此得第二主成分。- 一般若 Y 1 , Y 2 , . . . , Y k − 1 Y_1,Y_2,...,Y_{k-1} Y1,Y2,...,Yk−1还不够,则继续作
Y k = a 2 T X = a k 1 X 1 + a k 2 X 2 + . . . + a k p X p Y_k=a_2^TX=a_{k1}X_1+a_{k2}X_2+...+a_{kp}X_p Yk=a2TX=ak1X1+ak2X2+...+akpXp
s . t . { max V a r ( Y 1 ) = V a r ( a 1 T X ) = a 1 T Σ a 1 a 1 T a 1 = 1 C o v ( Y k , Y i ) = a k T Σ a i = 0 , i = 1 , . . , k − 1 ( 和前面的向量不相关 ) s.t.\quads.t.⎩ ⎨ ⎧maxVar(Y1)=Var(a1TX)=a1TΣa1a1Ta1=1Cov(Yk,Yi)=akTΣai=0,i=1,..,k−1(和前面的向量不相关){ max V a r ( Y 1 ) = V a r ( a 1 T X ) = a 1 T Σ a 1 a 1 T a 1 = 1 C o v ( Y k , Y i ) = a k T Σ a i = 0 , i = 1 , . . , k − 1 ( 和 前 面 的 向 量 不 相 关 )
由此得第k主成分。计算过程
- 具体的证明过程不在此作详细阐述。



主成分回归分析
- 主成分回归分析是为了克服最小二乘法(LS)估计在数据矩阵存在多重共线性时表现出的不稳定性质而提出的
- 主成分回归分析选择其中一部分重要的主成分作为新的自变量,丢弃了一部分影响不大的自变量,实际上达到了降维的目的,然后用最小二乘法对选取主成分后的模型进行参数估计,最后再变换回原来的模型求出参数的估计
案例


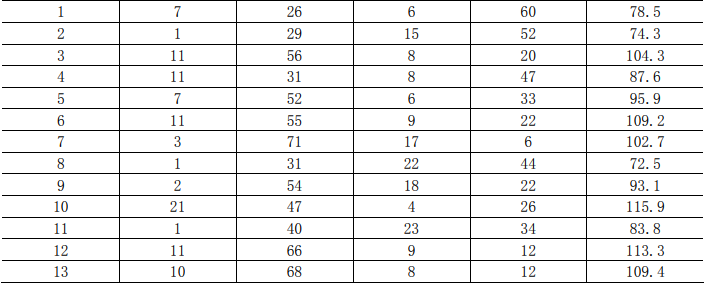
- x 0 = ( 13 , 4 ) y 0 = ( 12 , 1 ) x0=(13,4)\quad y0=(12,1) x0=(13,4)y0=(12,1)
- 标准化 x d = ( 13 , 4 ) y d = ( 12 , 1 ) xd=(13,4)\quad yd=(12,1) xd=(13,4)yd=(12,1)
- 进行主成分,vec2=(4×4)的每一列是特征向量,df=xd*vec2=(13×4)的一行就是一个样本在不同主成分上的得分(也就是原来的xd经过变换得到的新的数据df)
- 选择三个主成分:
[ z 1 z 2 z 3 ] 3 × 1 = v e c 2 [ : , 1 : 3 ] ( 3 × 4 ) T ∗ [ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] 4 × 1
_{3\times 1} =vec2[:,1:3]^T_{(3×4)}*[ z 1 z 2 z 3 ] _{4\times 1} ⎣ ⎡z1z2z3⎦ ⎤3×1=vec2[:,1:3](3×4)T∗⎣ ⎡x~1x~2x~3x~4⎦ ⎤4×1[ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ]
则df的前三列进行回归 y ^ = b _ c p a 1 × 3 T ∗ [ z 1 z 2 z 3 ] 3 × 1 \hat y=b\_cpa^T_{1\times 3}*_{3\times 1} y^=b_cpa1×3T∗⎣ ⎡z1z2z3⎦ ⎤3×1[ z 1 z 2 z 3 ] - 化成标准化回归即 z → x ~ z\to \tilde x z→x~
y ^ = b _ c p a ( 1 × 3 ) T ∗ v e c 2 [ : , 1 : 3 ] ( 3 × 4 ) T ∗ [ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] 4 × 1 = b _ s t d _ c p a ( 1 × 4 ) T ∗ [ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] 4 × 1 \hat y=b\_cpa^T_{(1\times 3)}*vec2[:,1:3]^T_{(3×4)}*
_{4\times 1}=b\_std\_cpa^T _{(1\times 4)}*[ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] _{4\times 1} y^=b_cpa(1×3)T∗vec2[:,1:3](3×4)T∗⎣ ⎡x~1x~2x~3x~4⎦ ⎤4×1=b_std_cpa(1×4)T∗⎣ ⎡x~1x~2x~3x~4⎦ ⎤4×1[ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] - 恢复到原始变量,即 x ~ → x \tilde x \to x x~→x
[ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] 4 × 1 = ( [ x 1 x 2 x 3 x 4 ] 4 × 1 − m e a n ( x 0 ) ( 1 × 4 ) ) . / s t d ( x 0 )
_{4\times 1} = ([ x ~ 1 x ~ 2 x ~ 3 x ~ 4 ] _{4\times 1} -mean(x0)_{(1\times 4)})./{std(x0)} ⎣ ⎡x~1x~2x~3x~4⎦ ⎤4×1=(⎣ ⎡x1x2x3x4⎦ ⎤4×1−mean(x0)(1×4))./std(x0)[ x 1 x 2 x 3 x 4 ]
y ^ = [ y − m e a n ( y 0 ) ] . / s t d ( y 0 ) \hat y=[y-mean(y0)]./std(y0) y^=[y−mean(y0)]./std(y0)
[ y − m e a n ( y 0 ) ] . / s t d ( y 0 ) = b _ s t d _ c p a ( 1 × 4 ) T ∗ ( [ x 1 x 2 x 3 x 4 ] 4 × 1 − m e a n ( x 0 ) ( 1 × 4 ) ) . / s t d ( x 0 ) [y-mean(y0)]./std(y0)=b\_std\_cpa^T _{(1\times 4)}*(_{4\times 1} -mean(x0)_{(1\times 4)})./{std(x0)} [y−mean(y0)]./std(y0)=b_std_cpa(1×4)T∗(⎣ ⎡x1x2x3x4⎦ ⎤4×1−mean(x0)(1×4))./std(x0)[ x 1 x 2 x 3 x 4 ]
y = m e a n ( y 0 ) − s t d ( y 0 ) ∗ m e a n ( x 0 ) . / s t d ( x 0 ) ∗ b _ s t d _ c p a + s t d ( y 0 ) ∗ b _ s t d _ c p a T . / s t d ( x 0 ) ∗ x y=mean(y0)-std(y0)*mean(x0)./std(x0)*b\_std\_cpa\\+std(y0)*b\_std\_cpa^T./std(x0)*x y=mean(y0)−std(y0)∗mean(x0)./std(x0)∗b_std_cpa+std(y0)∗b_std_cpaT./std(x0)∗xclc,clear load sn.txt [m,n]=size(sn); x0=sn(:,[1:n-1]); y0=sn(:,n); r=corrcoef(x0); %计算相关系数矩阵 xd=zscore(x0); %对设计矩阵进行标准化处理 yd=zscore(y0); %对y0进行标准化处理 %% 普通的回归 [b,BINT,R,RINT,STATS] = regress(y0,[ones(m,1),x0],0.05);%b=XY^{-1} % BINT 回归系数的估计区间 % R 残差 % RINT 置信区间 % STATS 用于检验回归模型的统计量。有4个数值:判定系数r2r2,F统计量观测值,检验的p的值,误差方差的估计 % 越接近1,回归方程越显著;时拒绝,F越大,回归方程越显著;时拒绝 % ALPHA 显著性水平(缺少时默认0.05) %% 1.主成分回归 [vec1,lamda,rate]=pcacov(r); %vec1为r的特征向量,lamda为r的特征值,rate为各个主成分的贡献率 contr=cumsum(rate); %计算累积贡献率,第i个分量表示前i个主成分的贡献率 %书上这一步不懂为什么要这样干?????希望有人能帮忙解答一下 f=repmat(sign(sum(vec1)),size(vec1,1),1); %构造与vec1同维数的元素为±1的矩阵 vec2=vec1.*f %修改特征向量的正负号,使得特征向量的所有分量和为正 df=xd*vec2; %计算所有主成分的得分 num=input('请选项主成分的个数:'); %通过累积贡献率交互式选择主成分的个数 b_cpa=df(:,[1:num])\yd; %主成分变量的回归系数,这里由于数据标准化,回归方程的常数项为0 %% 2.标准化的主成分回归 b_std_cpa=vec2(:,1:num)*b_cpa; %标准化变量的回归方程系数 %% 3.逆标准化(原始)的主成分回归 b_=[mean(y0)-std(y0)*mean(x0)./std(x0)*b_std_cpa, std(y0)*b_std_cpa'./std(x0)]; %计算原始变量回归方程的系数 %% 下面计算两种回归分析的剩余标准差 rmse1=sqrt(sum((b(1)+x0*b(2:end)-y0).^2)/(m-n)); %拟合了n个参数 rmse1 = 2.4460 rmse2=sqrt(sum((b_(1)+x0*b_(2:end)'-y0).^2)/(m-num)); %拟合了num个参数 rmse2 = 2.2029- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
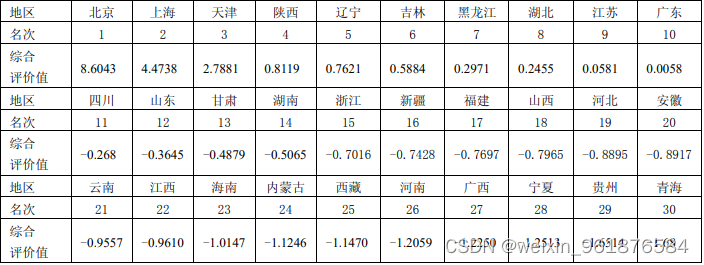
主成分分析案例——各地区普通高等教育发展水平综合评价
clc,clear load gj.txt %把原始数据保存在纯文本文件gj.txt中 gj=zscore(gj); %数据标准化 r=corrcoef(gj); %计算相关系数矩阵 %下面利用相关系数矩阵进行主成分分析,vec1的列为r的特征向量,即主成分的系数 [vec1,lamda,rate]=pcacov(r); %lamda为r的特征值,rate为各个主成分的贡献率 contr=cumsum(rate); %计算累积贡献率 f=repmat(sign(sum(vec1)),size(vec1,1),1);%构造与vec1同维数的元素为±1的矩阵 vec2=vec1.*f; %修改特征向量的正负号,使得每个特征向量的分量和为正 num=4; %num为选取的主成分的个数 df=gj*vec2(:,1:num); %计算各个主成分的得分 tf=df*rate(1:num)/100; %计算综合得分 [stf,ind]=sort(tf,'descend'); %把得分按照从高到低的次序排列 stf=stf'; ind=ind';- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
-
相关阅读:
yolov8-ros目标检测---硬件与仿真环境中区别
在React中,什么是组件的状态(state)?如何更新组件的状态?
视觉化洞察:为什么我们需要数据可视化?
基于脑电信号的癫痫发作预测
Vue学习——props(23)
基于springboot实现家具网站设计与实现平台项目【项目源码+论文说明】
APP备案公钥、证书MD5指纹/签名MD5值获取方法
GEO生信数据挖掘(五)提取临床信息构建分组,分组数据可视化(绘制层次聚类图,绘制PCA图)
什么是闭包?闭包详解
被 CSDN,伤透了心
- 原文地址:https://blog.csdn.net/weixin_45775970/article/details/126245187
